传感器融合-路面坡度计算
概述
本文主要介绍一种计算车辆坡度角的方法,利用有限的两轴加速度传感器并结合车辆动力学特性,实时估算车辆的坡度角。

融合框架
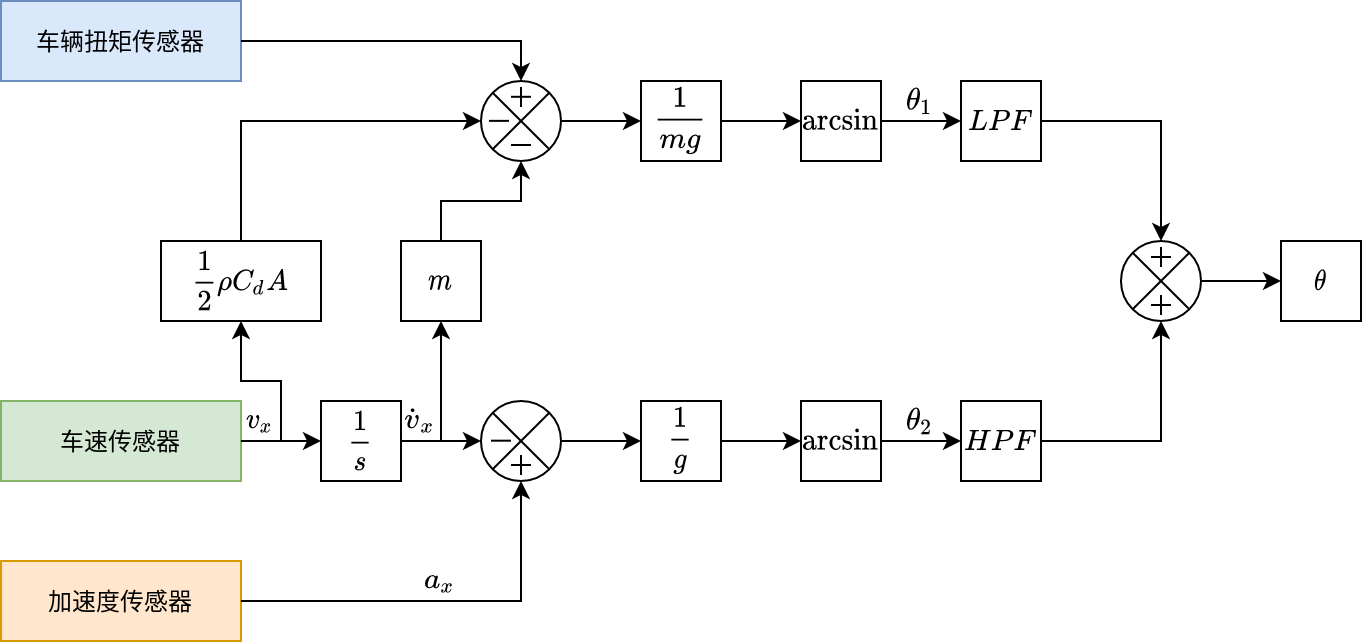
基于加速度偏差坡度估计
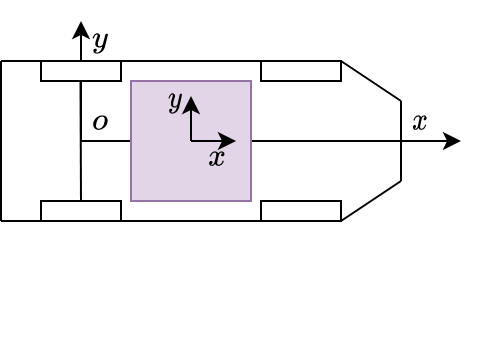
车辆坐标系定义
车辆坐标下定义如下:

沿车辆中轴线确定\(x\)轴,车头方向为正方向; \(x\)轴与后轴的交点为原点\(o\),过点\(o\)作一条直线与\(x\)轴垂直,将该直线定义为\(y\)轴,沿\(x\)轴逆时针方向为正。
加速度计定义
一般车辆加速度计的安装与车辆坐标系一致,车辆前进时,加速前进,传感测量值为正;减速前进,传感器测量值为负。车辆后退时,加速后退,传感器输出值为负;减速后退,传感器输出值为正。
同理,如果车辆前进上坡,静止在坡道上,传感器输出信号为正值;车辆前进下坡,静止在坡道上,传感器输出信号为负值。
计算坡度值
上坡静止状态
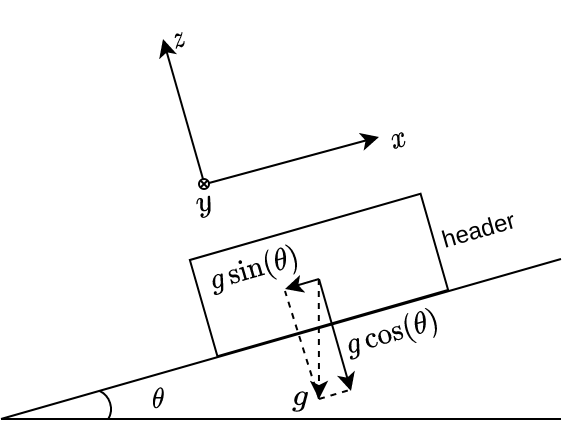
如上图所示,车辆上坡阶段,静止于坡道上时,加速度传感器在\(x\)轴上存在重力分量,可以表示为 \[ a_x = g\sin(\theta) \tag{1} \]
下坡静止状态
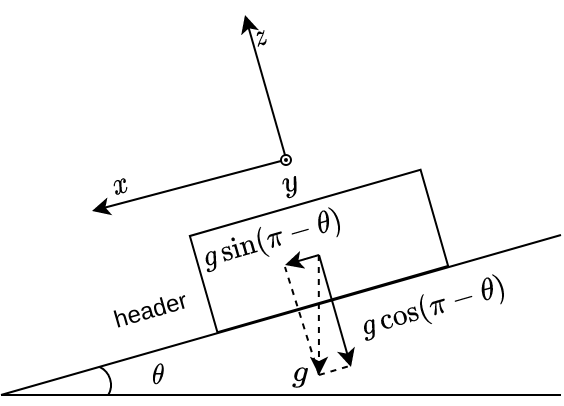
如上图所示,车辆下坡阶段,静止于坡道上时,加速度传感器在\(x\)轴上存在重力分量,可以表示为 \[ a_x=g\sin(\pi -\theta)=g\sin(-\theta) \tag{2} \]
车辆加速度
如上图所示,通过采集相邻时刻\(k-1\)和\(k\)的纵向速度,计算车辆\(k-1\)时刻的加速度为 \[ \dot{v}_x(k-1) = \frac{v(k) - v(k-1)}{\Delta T} \tag{3} \] 其中,\(\Delta T\)为采样步长,\(v(k)\)定义前进为正,后退为负。
坡度角计算
基于车辆在坡道上的受力分析,可以推算出当车辆运动时,加速度传感器输出信号\(a_x\)与坡度角\(\theta\)的关系如下: \[ a_x = \dot{v}_x + g\sin(\theta) \tag{4} \] 所以坡度角可以表示如下: \[ \theta = \arcsin(\frac{a_x - \dot{v}_x}{g}) \tag{5} \]
基于纵向动力学坡度计算
车辆纵向动力学模型

如上图所示,车辆纵向方向主要受到发动机产生的牵引力\(F_x\)的影响,同时也受到重力分量、迎风阻力和地面摩擦力的影响。通过对车辆对上述力的分析,车辆的动力学模型可以表示如下:
\[ F_x - mg\sin(\theta) - fmg\cos(\theta) - \frac{1}{2}\rho C_dAv_x^2 = m\dot{v}_x\tag{6} \]
其中,\(m\)为车辆质量,\(\rho\)为空气密度,\(C_d\)为风阻系数,\(A\)为迎风面积,\(g\)为重力加速度,\(\theta\)为路面坡度,\(f\)为路面滚阻系数。上述等式(6)中,路面坡度\(\theta\)为待求参数,其它参数对于某一车辆来说均可以认为是已知的或者通过测量能够得到。
令 \(y = F_x\),\(u = m\dot{v}_x + \frac{1}{2}\rho C_dAv_x^2\),\(b = mg(\sin(\theta) + f\cos(\theta))\),将公式(6)简化为:
\[ y = u + b \tag{7} \]
上式中,\(y\)、\(u\)为已知量,\(b\)为未知量,由于\(b\)是参数\(\theta\)的函数,因此对路面坡度的估计可以通过估算\(\hat{b}\)的值求得。
参数估计
采用带有遗忘因子的最小二乘法估计\(b\)的值,假设代价函数为\(V(\hat{b},k)\),那么采用最小二乘法估计\(b\)的值,相当于求解参数\(\hat{b}\),使得函数\(V(\hat{b},k)\)在某一时刻\(k\)取得最小值。
\[ V(\hat{b},k) = \frac{1}{2}\sum_{i=1}^{k} \lambda^{k-i}(y_i - u_i - \hat{b}_k)^2 \tag{8} \]
其中,\(\lambda\)为遗忘因子,\(k\)为采样时刻。
函数极小值的计算可以通过求解函数导数为0的参数,及
\[ \frac{\partial V}{\partial \hat{b}_k} = 0 \tag{9} \]
结合等式(8)、(9)得
\[ \sum_{i=1}^{k}\lambda^{k-i}(y_i - u_i - \hat{b}_k)=0\tag{10} \]
对等式(10)化简得
\[ \sum_{i=1}^{k}\lambda^{k-i}(y_i-u_i) - \sum_{i=1}^{k}\lambda^{k-i}\hat{b}_k=0 \tag{11} \]
移项得
\[ \hat{b}_k \sum_{i=1}^{k}\lambda^{k-i} =\sum_{i=1}^{k}\lambda^{k-i}(y_i-u_i) \tag{12} \]
基于等式(12),提取\(\hat{b}_k\)得
\[ \hat{b}_k = (\sum_{i=1}^{k}\lambda^{k-i})^{-1}\bigl(\sum_{i=1}^{k}\lambda^{k-i}(y_i-u_i)\bigr) \tag{13} \]
从等式(13)可以看出,随着采样时刻\(k\)不断增加,估计值\(\hat{b}\)的计算量也不断增加。由于车辆行驶过程中的路面坡度估计需要实时计算,因此在实际应用中一般采用递推最小二乘估计来实时估计每一采样时刻\(b\)的估计值\(\hat{b}\)。
\[ \hat{b}_k = \hat{b}_{k-1} + L_k(y_k -u_k)\tag{14} \]
增益系数\(L_k\)为
\[ L_k = \frac{P_{k-1}}{\lambda + P_{k-1}} \tag{15} \]
误差协方差\(P_k\)为
\[ P_k = \frac{1}{\lambda}(1 - L_k)P_{k-1} \tag{16} \]
根据公式(14)、(15)、(16)的更新过程
\[ D = \frac{\hat{b}}{mg} \tag{17} \]
坡度角为
\[ \theta = \arcsin(\frac{D-f\sqrt{1-D^2 + f^2}}{1 + f^2}) \tag{18} \]
坡度角融合
车辆行驶过程中路面坡度\(\theta\)可以认为是高频信号和低频信号两部分组成,在对路面坡度进行估计时,基于纵向动力学估计方法依赖于车辆的多个参数,车辆的各个参数受高频噪声影响大;基于加速度偏差坡度估计的缺点是受惯性传感器的静态偏差影响较大,惯性传感器的静态偏差属于低频噪声,为了保证路面坡度估算结果的准确性,对\(\theta_1\)采用低通滤波器除去其高频部分,对\(\theta_2\)采用高通滤波器滤除其低频部分,最终得到更加准确的实时估计值\(\hat{\theta}\)为:
\[ \hat{\theta} = \frac{1}{\tau s + 1}\theta_1 + \frac{\tau s}{\tau s + 1}\theta_2 \tag{19} \]
其中,\(\tau\)为时间常数,\(s\)为拉普拉斯算子,\(\frac{1}{\tau s + 1}\)为低通滤波器,\(\frac{\tau s}{\tau s + 1}\)为高通滤波器。