路径规划-ReedsShepp曲线
概述
ReedsShepp算法简称RS,由 J.AReeds和L.A.Sheep于1990年发表的论文(optimal path for a car that goes both forward and backwards)。该方法基于Dubins算法进行改进,将反向运动加入到规划中,这就使得在某些情况下可以得出比Dubins曲线更优的解。

曲线
Dubins曲线
关于Dubins曲线,不考虑车辆后退,且不允许出现尖瓣。Dubins给出了充分的路径集合,该集合里所包含的曲线叫做测地线或最佳路径。但是这个充分集合很小,对于每种特定终点情况下的集合中,最多只有6个可选曲线,分别表示如下:
\[ \begin{array}{cl} \{&LRL &LSL &LSR &RLR &RSR &RSL &\} \tag{1} \end{array} \]
其中等式(1)中符号含义如下:
| 符号 | 含义 | 绕单位圆 |
|---|---|---|
| L | 左转 | 逆时针 |
| R | 右转 | 顺时针 |
| S | 直走 | 直走 |
Dubins证明,一个最优路径一定是由分段圆弧(单位圆)和线段组成的平滑曲线,且最多3部分组成。可以进一步简化表示为如下形式:
\[ \begin{array}{cl} CCC&\to&\{&LRL &RLR &&&\} \\ CSC&\to&\{&LSL &RSR &LSR &RSL&\} \end{array} \tag{2} \]
等式(2)中符号含义如下:
| 符号 | 含义 |
|---|---|
| C | 单位圆弧 |
| S | 一条直线段 |
一个字段表示相应的一类路径,使用文字符号的下标指定相应弧长和线段的长度,比如\((L_tS_uR_v)\)。
ReedSHeep曲线
在ReedSHeep曲线的路径中,允许尖瓣存在。为了表示,需要在字段中的字母上加入上标,用来表示运动方向,表示如下:
| 符号 | 含义 | 绕单位圆 |
|---|---|---|
| \[L^+\] | 向前左转 | 逆时针 |
| \[L^-\] | 向后左转 | 顺时针 |
| \[R^+\] | 向前右转 | 逆时针 |
| \[R^-\] | 向后右转 | 顺时针 |
| \[S^+\] | 向前直走 | / |
| \[S^-\] | 向后直走 | / |
例如:\(L^+R^-\)拥有一个尖瓣而\(L^+R^+\)无尖瓣。
在车辆中,字母L、R、S参考方向盘转角,符号\(+\)和\(-\)参考挡位切换
使用C、S字符可以给出如下集合:
\[ \begin{array}{cl} CCC \gets \{&C^+C^-C^+ &C^+C^-C^- &C^+C^+C^- &C^+C^+_uC^-_uC^- &C^+C^-_uC^-_uC^+&\}\\ CSC \gets \{&C^+S^+C^+ &C^-C^+_{\pi/2}S^+C^+ &C^+S^+C^+_{\pi/2}C^- &C^-C^+_{\pi/2}S^+C^+_{\pi/2}C^-&&\} \end{array}\tag{3} \]
以及通过反转等式(3)的符号可以获得新的的字段。上式(3)中,\(C\)表示\(L\)或者\(R\),\(C^+_{\pi/2}\)表示相应的\(L\)或\(R\)的弧长为\(\pi/2\),\(C_uC_u\)组合表示相应的弧段拥有相等的长度。
下标符号
为了更加缜密表示,在\(C^\pm_t,L^\pm_t,R^\pm_t,S^\pm_t\)中使用有点多余的约定,规定\(t\)的符号与方向匹配。
如果\(t > 0\):车辆前进,符号\(+\) 如果\(t<0\):车辆后退,符号\(-\)
自由参数数量
在等式(3)的曲线族中,\(C^+_tC^-_uC^-_vC^+_w\)具有自由参数\((t,u,v,w)\)的数量比最终情形的数量多一个。优化路径族通过给定额外的方程式,例如\(u=v\)或者\(v = \pi/2\)。确保等式(3)中的每个情形只有3个自由参数。
紧凑表示
为了以紧凑的表示,避免\(\pm\),可以写出充分路径的列表如下:
\[ \begin{array}{cl} CCC \gets \{&C\mid C\mid C &C\mid CC &CC\mid C &CC_u\mid C_uC &C\mid C_uC_u\mid C&\}\\ CSC \gets \{&CSC &C\mid C_{\pi/2}SC &CSC_{\pi/2}\mid C &C\mid C_{\pi/2}SC_{\pi/2}\mid C&&\}\\ \end{array}\tag{4} \]
其中,\(|\)表示方向反转。当等式(3)和(4)中的\(C\)被替换为\(C = L\)或\(C=R\),共有48种字段,以\(L^\pm,R^\pm,S^\pm\)的形式表示。这48个字段中的一些对于字段类型的实际路径存在两种公式。对于给定的任意情形,至多68个公式。
任何长度小于\(\pi/8\)的最佳路径一定是\(CSC\)形式。很容易得出结论,任何最佳路径一定是由\(C\)和\(S\)的字段组成。使用一系列的特殊参数,可将所有有限的字段简化为\(CCC\)或\(CSC\)的形式。
充分集合
下表列出了充分集合中的48个字段,以及相应的缩写形式\(C \mid C\)和\(C^\pm\),最后一列给出了给定字段的长度公式。
| 形式\(C\mid C\) | 形式\(C^\pm\) | 明确表示 |
|---|---|---|
| \[ \begin{array}{cl} C\mid C \mid C \end{array} \] | \[ \begin{array}{cl} &C^+C^-C^+ \\&C^-C^+C^- \end{array} \] | \[ \begin{array}{cl}&L^+R^-L^+ &R^+L^-R^+ \\ &L^-R^+L^- &R^-L^+R^- \end{array} \] |
| \[ \begin{array}{cl}C \mid CC \end{array}\] | \[ \begin{array}{cl}&C^+C^-C^- \\&C^-C^+C^+ \end{array} \] | \[ \begin{array}{cl}&L^+R^-L^- &R^+L^-R^-\\&L^-R^+L^+ &R^-L^+R^+ \end{array} \] |
| \[ CC \mid C \] | \[ \begin{array}{cl}&C^+C^+C^- \\&C^-C^-C^+ \end{array} \] | \[ \begin{array}{cl}&L^+R^+L^- &R^+L^+R^-\\&L^-R^-L^+ &R^-L^-R^+ \end{array} \] |
| \[ CC_u \mid C_uC \] | \[ \begin{array}{cl}&C^+C^+_uC^-_{-u}C^- \\&C^-C^-_{-u}C^+_uC^+ \end{array} \] | \[ \begin{array}{cl}&L^+R^+_uL^-_{-u}R^- &R^+L^+_uR^-_{-u}L^-\\&L^-R^-_{-u}L^+_uR^+ &R^-L^-_{-u}R^+_uL^+ \end{array} \] |
| \[ C \mid C_uC_u \mid C \] | \[ \begin{array}{cl}&C^+C^-_{-u}C^-_{-u}C^+ \\&C^-C^+_{u}C^+_uC^- \end{array} \] | \[ \begin{array}{cl}&L^+R^-_{-u}L^-_{-u}R^+ &R^+L^-_{-u}R^-_{-u}L^+\\&L^-R^+_{u}L^+_uR^- &R^-L^+_{u}R^+_uL^-\end{array} \] |
| \[ CSC \] | \[ \begin{array}{cl}&C^+C^+C^+ \\&C^-C^-C^-\end{array} \] | \[ \begin{array}{cl}&L^+S^+L^+ &R^+S^+R^+\\&L^+S^+R^+ &R^+S^+L^+\\&L^-S^-L^- &R^-S^-R^-\\&L^-S^-R^- &R^-S^-L^-\end{array} \] |
| \[ C \mid C_{\pi/2}SC \] | \[ \begin{array}{cl}&C^+C^-_{-\pi/2}S^-C^- \\&C^-C^+_{\pi/2}S^+C^+\end{array} \] | \[ \begin{array}{cl}&L^+R^-_{-\pi/2}S^-L^- &R^+L^-_{-\pi/2}S^-R^-\\&L^+R^-_{-\pi/2}S^-R^- &R^+L^-_{-\pi/2}S^-L^-\\&L^-R^+_{\pi/2}S^+L^+ &R^-L^+_{\pi/2}S^+R^+\\&L^-R^+_{\pi/2}S^+R^+ &R^-L^+_{\pi/2}S^+L\\\end{array} \] |
| \[ CSC_{\pi/2} \mid C \] | \[ \begin{array}{cl}&C^+S^+C^+_{\pi/2}C^- \\&C^-S^-C^-_{\pi/2}C^+\end{array}\] | \[\begin{array}{cl}&L^+S^+R^+_{\pi/2}L^- &R^+S^+L^+_{\pi/2}R^-\\&R^+S^+R^+_{\pi/2}L^- &L^+S^+L^+_{\pi/2}R^-\\&L^-S^-R^-_{-\pi/2}L^+ &R^-S^-L^-_{-\pi/2}R^+\\&R^-S^-R^-_{-\pi/2}L^+ &L^-S^-L^-_{-\pi/2}R^+ \end{array} \] |
| \[ C\mid C_{\pi/2}SC_{\pi/2}C \] | \[ \begin{array}{cl}&C^+C^-_{-\pi/2}S^-C^-_{-\pi/2}C^+ \\&C^-C^+_{\pi/2}S^+C^+_{\pi/2}C^-\end{array}\] | \[\begin{array}{cl}&L^+R^-_{-\pi/2}S^-L^-_{-\pi/2}R^+ &R^+L^-_{-\pi/2}S^-R^-_{-\pi/2}L^+\\&L^-R^+_{\pi/2}S^+L^+_{\pi/2}R^- &R^-L^+_{\pi/2}S^+R^+_{\pi/2}L^-\end{array} \] |
允许路径
根据车辆运动学模型的微分方程如下:
\[ \begin{array}{cl} \dot{x}(t) &= V(t)\cos\bigl(\psi(t)\bigr) \quad\\ \dot{y}(t) &= V(t)\sin\bigl(\psi(t)\bigr) \quad\\ \dot{\psi}(t) &= \dfrac{V(t)}{R(t)} \end{array}\tag{5} \]
为了更好的表示路径,对车辆行驶路径进行归一化处理,简化路径的表示方法。即限制\(V(t)= \pm1\)、\(|\dot{\psi}(t)| =1\),所以车辆只能在自身方向\(\psi(t)\)上以速度\(|V(t)=1|\)前进或后退,并且变化率\(\dot{\psi}(t)\leq1\)rad/s。对于车辆的转弯半径可以通过缩放变换到1,即车辆绕单位圆行驶。这样表示的好处在于车辆行驶的弧长与变化的角度一致。如果直线行驶,则\(\dot{\psi}(t) = 0\),令\(\dot{\psi}\)
其积分形式如下:
\[ \begin{array}{cl} x(t) &= x(0) + \int^t_0V(\tau)\cos\bigl(\psi(\tau)\bigr)d\tau\\ y(t) &= y(0) + \int^t_0V(\tau)\sin\bigl(\psi(\tau)\bigr)d\tau\\ \psi(t) &= \psi(0) + \int^t_0\dot{\psi}(\tau)d\tau \end{array}\tag{6} \]
一个允许的路径或者曲线可以表示成函数\(\gamma(t) = \bigl(x(t),y(t),\psi(t)\bigr)\)的形式。对于任意曲线从\(t_0\)到\(t_1\),其中\(t_0 < t_1\),\(\gamma(t_0) = a\),\(\gamma(t_1)=b\),则路径的长度为\(L(\gamma)= t_1 - t_0\)。所以关于最短路径的问题,就转换为求取对于任意a和b\(\in \Re^3\),使得\(L(\gamma)\)最小的\(\gamma\)。
可行路径
对于时间\(t \in \Re\),使用
\[ \begin{array}{cl} L_t:\Re^3 \to \Re^3\\ R_t: \Re^3 \to \Re^3\\ S_t: \Re^3 \to \Re^3 \end{array}\tag{7} \]
表示单位圆\(L_t\)或\(R_t\)和线段\(S_t\)的位置和方向信息,起始坐标表示为\((x,y,\psi)\),所以经过时间\(t\),根据等式(6)积分得:
\[ \begin{array}{cl} x(t) &= x + \sin(\tau)|^{\psi+t}_{\psi}\\ y(t) &= y - \cos(\tau)|^{\psi+t}_{\psi}\\ \psi(t) &= t \end{array} \]
对应的路径如下:
\[ \begin{array}{cl} L_t^+(x,y,\psi) &= \bigl(x + \sin(\psi+t)- \sin(\psi),y - \cos(\psi+t)+\cos(\psi),\psi + t\bigr)\\ R_t^+(x,y,\psi) &= \bigl(x - \sin(\psi-t)+ \sin(\psi),y + \cos(\psi-t)-\cos(\psi),\psi - t\bigr)\\ S_t^+(x,y,\psi) &= (x+t\cos(\psi),y + t\sin(\psi),\psi) \end{array}\tag{8} \]
\[ \begin{array}{cl} L_t^-(x,y,\psi) &= \bigl(x - \sin(\psi-t)+ \sin(\psi),y + \cos(\psi-t)-\cos(\psi),\psi - t\bigr)\\ R_t^-(x,y,\psi) &= \bigl(x + \sin(\psi+t)- \sin(\psi),y - \cos(\psi+t)+\cos(\psi),\psi + t\bigr)\\ S_t^-(x,y,\psi) &= (x-t\cos(\psi),y - t\sin(\psi),\psi) \end{array} \]
- 举例
假设一个曲线\(L^+_tR^-_uS^-_vL^-_w\),起始于点\((0,0,0)\),一定终止于
\[ \bigl(X(t,u,v,w),Y(t,u,v,w),\Psi(t,u,v,w)\bigr)= R_w(S_v(R_u(L_t(0,0,0)))) \]
其长度为\(L(t,u,v,w) = |t|+ |u| + |v| + |w|\)。
位置姿态统一
由于车辆的起始位置和终点位置无法穷举,所以一般在计算路径之前,需要将车辆的位置和姿态作归一化:
| 类型 | 坐标 |
|---|---|
| 起始姿态 | \(( 0, 0, 0 )\) |
| 目标姿态 | \((x, y, \psi )\) |
| 转弯半径 | 1 |
假设起始姿态为\(q_i=(x_1,y_1,\psi_1)\),目标姿态为\(q_g=(x_2,y_2,\psi_2)\),车辆转弯半径为\(r=\rho\)。
- 平移
首先将向量\(\vec{q_iq_g}\)平移到远点\((0,0)\),平移向量为\((-x_1,-y_1)\)。则\(q_i\)平移到\((0,0)\),\(q_g\)平移到\((x_2-x_1,y_2-y_1)\),最终得到的平移向量:
\[ \vec{q_iq_g}= \left[ \begin{array}{cl} x_2-x_1\\ y_2-y_1 \end{array}\right]= \left[ \begin{array}{cl} x\\ y \end{array} \right]\tag{9} \]
- 旋转
应用旋转矩阵,将车辆的起始点朝向转到x轴正向,对应得旋转角度为\(\psi_1\),旋转矩阵如下:
\[ \left[ \begin{array}{cl} \cos(\psi_1) &\sin(\psi_1)\\ -\sin(\psi_1) &\cos(\psi_1) \end{array} \right]\tag{10} \]
则向量\(\vec{q_iq_g}\)旋转后得
\[ \vec{q_iq_g}= \left[ \begin{array}{cl} x\\ y \end{array} \right]= \left[ \begin{array}{cl} \cos(\psi_1) &\sin(\psi_1)\\ -\sin(\psi_1) &\cos(\psi_1) \end{array} \right] \left[ \begin{array}{cl} x\\ y \end{array} \right]= \left[ \begin{array}{cl} x\cos(\psi_1) + y\sin(\psi_1)\\ -x\sin(\psi_1)+y\cos(\psi_1) \end{array} \right] \tag{11} \]
通过上述旋转后,目标位置朝向为\(\psi = \psi_2 - \psi_1\)。
- 缩放
对于车辆的转弯半径\(\rho\),将车辆转向半径缩放到1,得到最终的车辆其实姿态为:
\[ q_i= \left[ \begin{array}{cl} 0\\ 0\\ 0 \end{array} \right]\tag{12} \]
目标姿态为:
\[ q_g= \left[ \begin{array}{cl} \bigl(x\cos(\psi_1) + y\sin(\psi_1)\bigr)/\rho\\ \bigl(-x\sin(\psi_1)+y\cos(\psi_1)\bigr)/\rho\\ \psi_2-\psi_1 \end{array} \right]\tag{13} \]
类型转换
上述48个字段中的某些方程的最小值拥有两个解,所以实际公式将达到68个。凭经验观察,似乎只要48个表达式在任何情况下都需要,一些表达式无疑是方程的虚假解。在可以考虑的48种不同的字符模式中,由于存在一些基本变换,没有必要给出所有的形式。下面列出3种常见的转换模式:
时间变换(timeflip)
时间变换通过交换字母上标符号\(+\)和\(-\),即车取反辆的行进方向。也就是说,\(L^-R^+S^+L^+\)表达式可以通过\(L^+R^-S^-L^-\)表达式通过时间变换获得。其中\(+\)和\(-\)交换。如果原始路径从\((0,0,0)\)到\((x,y,\psi)\),显而易见时间变换的路径将从\((0,0,0)\)到\((-x,y,-\psi)\)。因此,如果一个路径表达式\(L^+_tR^-_{-\pi/2}S^-_uL^-_v\)从点\((0,0,0)\)到\((-x,y,-\psi)\),查找的合适弧长为t、u、v。这就等效于路径表达式\(L^-_tR^+_{\pi/2}S^+_uL^+_v\)从点\((0,0,0)\)到\((x,y,\psi)\)查找相应的弧长。所以,通过时间变换将上述列表中第一个字母符号为"\(-\)"的字段消除。
反射变换(reflect)
反射变换通过交换字母\(L\)和\(R\),即取反车辆转向。也就是说,一个路径表达式\(R^+L^-S^-R^-\)的解可以通过反射变换从路径表达式\(L^+R^-S^-L^-\)的解中获得,即沿着该路径交换\(L\)和\(R\)。相应的参考路径由\((x,y,\psi)\)变为\((x,-y,-\psi)\)。
假设已知路径\(L^+_tR^-_{-\pi/2}S^-_uL^-_v\)解的表达式,从点\((0,0,0) \to (x,-y,-\psi)\)的最优弧长为t、u、v。
\[ \begin{array}{cl} &L^+_tR^-_{-\pi/2}S^-_uL^-_v :(0,0,0) \to (x,-y,-\psi)\\ \end{array} \]
则从点\((0,0,0) \to (x,y,\psi)\)的最优弧长为t、u、v,对应路径\(R^+_tL^-_{-\pi/2}S^-_uR^-_v\)的解,
\[ \begin{array}{cl} &R^+_tL^-_{-\pi/2}S^-_uR^-_v :(0,0,0) \to (x,y,\psi)\\ \end{array} \]
所以,通过反射变换可以将上述列表中以\(L^+\)开头的字段消除。
逆向变换(backwards)
逆向变换通过将原路径按照相反方向行走。也就是说,路径\(L^-S^-R^-L^+\)的公式可以使用逆向变换从路径\(L^+R^-S^-L^-\)的公式中获得,即按照相反的顺序运动。
逆向变换将目标点\((x,y,\psi)\)转化为\(\bigl(x\cos(\psi)+y\sin(\psi),x\sin(\psi)-y\cos(\psi),\psi\bigr)\)。所以可以通过公式\(L^+R^-S^-L^-\)到达点\(\bigl(x\cos(\psi)+y\sin(\psi),x\sin(\psi)-y\cos(\psi),\psi\bigr)\),从而获得\(L^-S^-R^-L^+\)到达点\((x,y,\psi)\)的解。
通过这个变换可以消除上述列表中一些字段,最终保留9个字段讨论如下。
公式计算
概述
通过上述3种变换,还剩9个公式需要求解。这9个表达式都是从点\((0,0,0)\)到点\((x,y,\psi)\),为了更加方便表述,定义如下符号:
- 极坐标
由笛卡尔坐标系\((x,y)\)与极坐标系的转化可以写为\((r,\theta) = R(x,y)\),展开如下:
\[ \begin{array}{cl} x = r \cdot\cos(\theta)\\ y = r \cdot\sin(\theta) \end{array}\leftrightharpoons \begin{array}{cl} r &= \sqrt{x^2 + y^2}\\ \theta &= \arctan(\dfrac{y}{x}) \end{array} \]
其中,\(r \geq 0\),\(-\pi \leq \theta < \pi\)。
- 偏航角标准化
通过标准化符号\(M\),即\(\psi = M(\theta)\),将\(\psi\)的范围限制在\(-\pi \leq \psi< \pi\)。
公式 \(L^+_tS^+_uL^+_v\)
- 推导
第一个公式详细推导计算过程,后面的公式由于原理相同,就不详细推导,直接给出结论。
推导过程,主要结合等式(8)种的结论:
\[ \begin{array}{cl} L_t^+(x,y,\psi) &= \bigl(x + \sin(\psi+t)- \sin(\psi),y - \cos(\psi+t)+\cos(\psi),\psi + t\bigr)\\ R_t^+(x,y,\psi) &= \bigl(x - \sin(\psi-t)+ \sin(\psi),y + \cos(\psi-t)-\cos(\psi),\psi - t\bigr)\\ S_t^+(x,y,\psi) &= (x+t\cos(\psi),y + t\sin(\psi),\psi) \end{array} \]
起始坐标\((0,0,0)\),目标坐标\((x,y,\psi)\)
| 操作 | \(x\) | \(y\) | \(\psi\) |
|---|---|---|---|
| 起始坐标 | 0 | 0 | 0 |
| 移动弧长t | \(\sin{t}\) | \(1 - \cos{t}\) | \(t\) |
| 移动弧长u | \(\sin{t} + u\cos{t}\) | \(1 - \cos{t} + u\sin{t}\) | \(t\) |
| 移动弧长v | \(u\cos{t} + \sin{(t+v)}\) | \(1 + u\sin{t} - \cos{(t + v)}\) | \(t + v\) |
| 终点坐标 | \(x\) | \(y\) | \(\psi\) |
从上述表格可知
\[ \begin{array}{cl} x &= u\cos{t} + \sin{(t+v)} \\ y &= 1 + u\sin{t} - \cos{(t + v)} \\ \psi &= t + v \end{array} \]
将$= t + v $带入得
\[ \begin{array}{cl} x &= u\cos{t} + \sin{\psi} \\ y &= 1 + u\sin{t} - \cos{\psi} \end{array} \]
移项得
\[ \begin{array}{cl} u\cos{t} &= x - \sin{\psi} \\ u\sin{t} &= y + \cos{\psi}- 1 \end{array} \]
使用极坐标表示得
\[ (u,t) = R(x - \sin{\psi},y + \cos{\psi}- 1) \]
则
\[ v = M(\psi - t) \]
- 结论
已知起始坐标\((0,0,0)\)和目标坐标\((x,y,\psi)\),则\(L^+_tS^+_uL^+_v\)的最优解为
\[ \begin{array}{cl} (u,t) &= R(x - \sin{\psi},y + \cos{\psi}- 1)\\ v &= M(\psi - t) \end{array} \]
总长度为\(L = |t| + |u| + |v|\)。
公式 \(L^+_tS^+_uR^+_v\)
下表描述了计算过程:
| 操作 | \(x\) | \(y\) | \(\psi\) |
|---|---|---|---|
| 起始坐标 | \(0\) | \(0\) | \(0\) |
| 移动弧长t | \(\sin{t}\) | \(1 - \cos{t}\) | \(t\) |
| 移动弧长u | \(\sin{t} + u\cos{t}\) | \(1 - \cos{t} + u\sin{t}\) | \(t\) |
| 移动弧长v | \(u\cos{t} - \sin{(t-v)}+2\sin{t}\) | \(1 + u\sin{t} + \cos{(t - v)}-2\cos{t}\) | \(t - v\) |
| 终点坐标 | \(x\) | \(y\) | \(\psi\) |
整理得
\[ \begin{array}{cl} x &= u\cos{t} - \sin{(t-v)}+2\sin{t} \\ y &= u\sin{t} + \cos{(t - v)}-2\cos{t} +1 \\ \psi &= t - v \end{array} \]
将\(\psi = t -v\)带入得
\[ \begin{array}{cl} x &= u\cos{t} - \sin{\psi}+2\sin{t} \\ y &= u\sin{t} + \cos{\psi}-2\cos{t} +1 \end{array} \]
移项得
\[ \begin{array}{cl} u\cos{t} &= x + \sin{\psi} - 2\sin{t} \\ u\sin{t} &= y - \cos{\psi} + 2\cos{t} -1 \end{array} \]
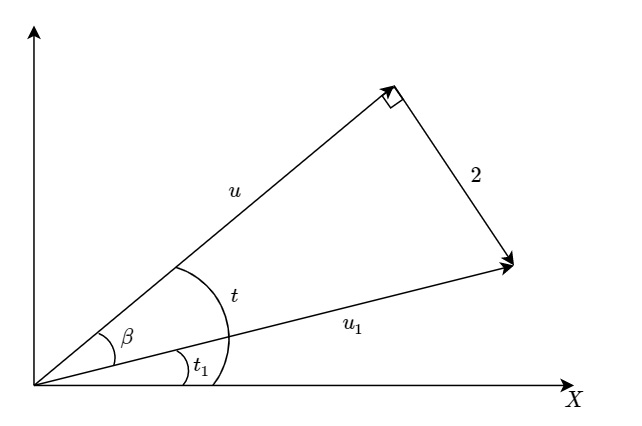
令$ P_1(u_1,t_1) = R(x + ,y - ) \(,\)P_2(2,t-)=R(2,-2)\(,\)P(u,t)=R(u,u)$。
由等式得
\[ P(u,t) = P_1(u_1,t_1) - P_2(2,t-\frac{\pi}{2}) \]
由上式可知,极向量\(P\)与\(P_2\)必须垂直,由于向量\(P_2\)的长度为2,为了满足上述关系,向量\(P_1\)的长度不能小于2,否则无解。
- 如果\(u_1^2 < 4\)
无解,\(L = \infty\)。
- 如果\(u_1^2 \geq 4\)
已知起始坐标\((0,0,0)\)和目标坐标\((x,y,\psi)\),可以求出\(P_1(u_1,t_1) = R(x + \sin\psi,y + \cos\psi -1)\),且\(P_2(2,t-\frac{\pi}{2})\)已知。根据上述极向量\(P\)、\(P_1\)、\(P_2\)之间的直角三角形关系,可得\(u^2 + 2^2 = u_1^2 \to u = \sqrt{u_1^2 - 4}\)。极向量\(P\)与\(P_1\)之间的夹角\(\beta = \arctan{\dfrac{2}{u}}\),故\(t = M(t_1 + \beta)\),\(v = M(t - \psi)\)。弧长\(L = |t| + |u| + |v|\)。
公式 \(L^+_tR^-_uL^+_v\)
下表是路径的计算过程。
| 操作 | \(x\) | \(y\) | \(\psi\) |
|---|---|---|---|
| 起始坐标 | \(0\) | \(0\) | \(0\) |
| 移动弧长t | \(\sin{t}\) | \(1 - \cos{t}\) | \(t\) |
| 移动弧长u | \(\sin(t + u)\) | \(1 - \cos{(t + u)}\) | \(t + u\) |
| 移动弧长v | \(\sin{(t+u + v)}\) | \(1 - \cos{(t + u + v)}\) | \(t +u+ v\) |
| 终点坐标 | \(x\) | \(y\) | \(\psi\) |