路径规划-AStar
概述
A*算法是一种基于图搜索的路径搜索算法,通过结合移动代价和启发代价,优化路径的搜索性能. 
算法描述
确定规划的起点和终点
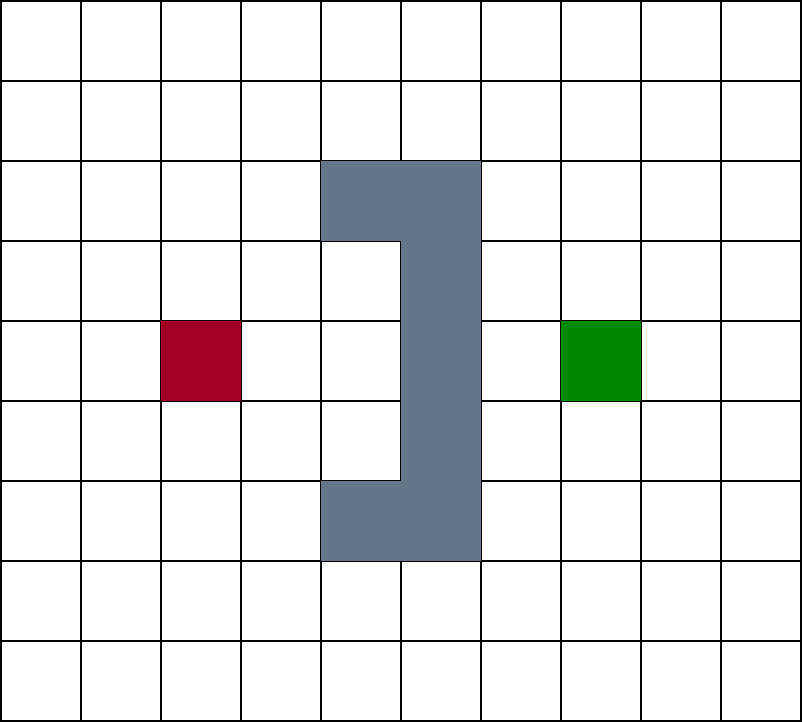
下图所示,红色方块代表规划起始点,绿色方块代表终点,深灰色方块代表障碍物区域,其余白色方块代表可行驶区域(free space).首先将起始点节点推送到open集合中.
产生临近节点
每次从open集合中取出总代价值最小的节点,由于当前open集合中只有起始节点,所以此时从open集合中取出的就是起始节点,并将该节点推入close集合.
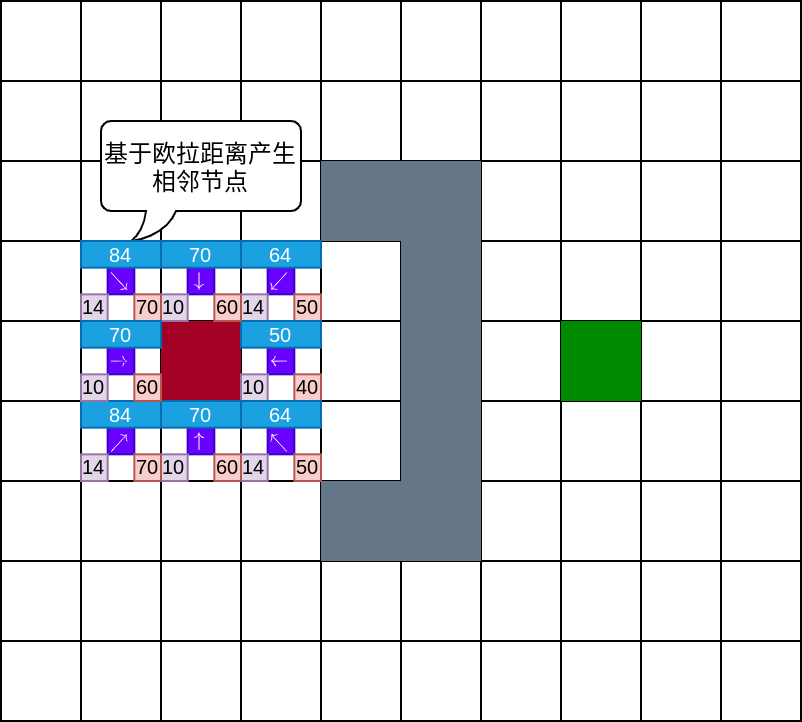
如下图所示,基于起始节点生成相邻节点,并计算每个节点的代价值.其中A*节点的代价值由移动代价和启发代价组成,即\(F = G + H\).
本例中,采用如下距离计算代价值:
- 移动代价 采用欧拉距离计算移动代价值
- 启动代价 采用曼哈顿距离计算启发代价值
图例说明
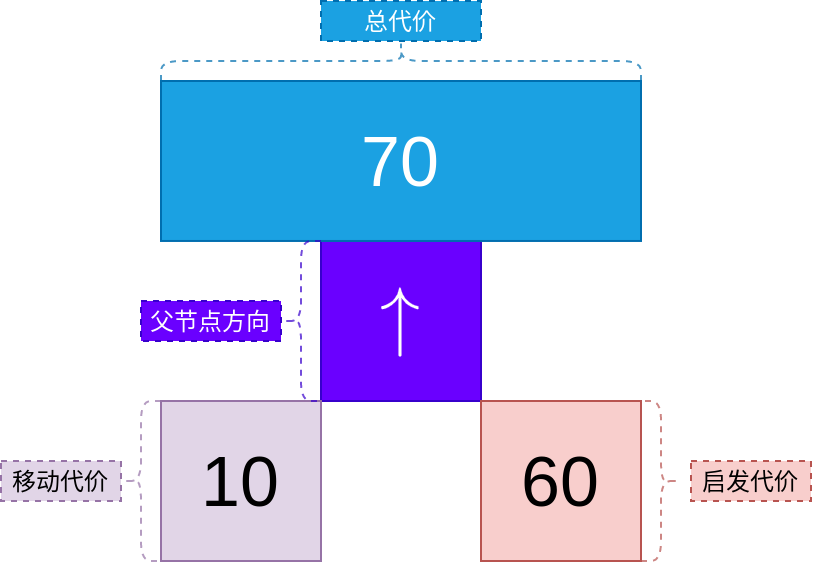
下图是对上图中每个节点中小方格的说明:
- 左下角的方格代表移动代价
- 右下角的方格代表启发代价
- 最上方的矩形方格代表总的代价值
- 中间的紫色方格代表父节点的方向
节点选择
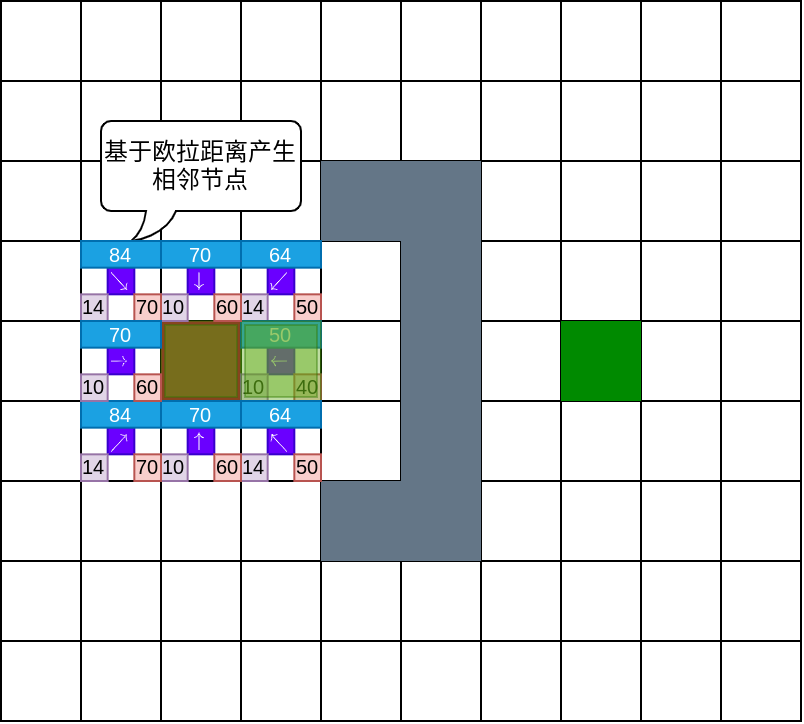
A*算法下一节点的选择,是从open集合中选取总代价值最小的节点.如下图所示,位于起始点右侧的节点代价值最小,图中使用浅绿色蒙板覆盖该节点表示选中.
节点扩展
基于选中的节点,根据扩展规则,生成新的临近节点,计算临近节点时只需要计算移动代价.
如下图中的右侧所示,对于新生成的8个节点需要做如下条件判断:
是否在close集合中:
如果该节点在close集合中,直接跳过该节点,进行下一节点的判断
是否碰撞:
若该节点与障碍物存在碰撞可能,则跳过该节点,进行下一节点的判断;
是否在open集合中:
如果该节点==在==open集合中,需要判断该节点的移动代价是否小于原先位置节点的移动代价:
如果小于,则替换原先节点,并将节点的父节点方向指向当前节点,否则跳过该节点,进行下一节点的判断.
如果该节点==不在==open集合,则直接将其加入open集合.
如下图所示,当前节点的左侧的节点已经在close集合中,直接跳过该节点;当前节点左上角,左下角,上方和下方的节点已经在open集合中,所以需要比较新节点与open集合中节点的移动代价.通过比较,这四个新节点的移动代价大于相应open集合中节点的移动代价,所以跳过这些节点;当前节点右侧三个新节点都不在open集合中,所以直接将它们推入open集合.
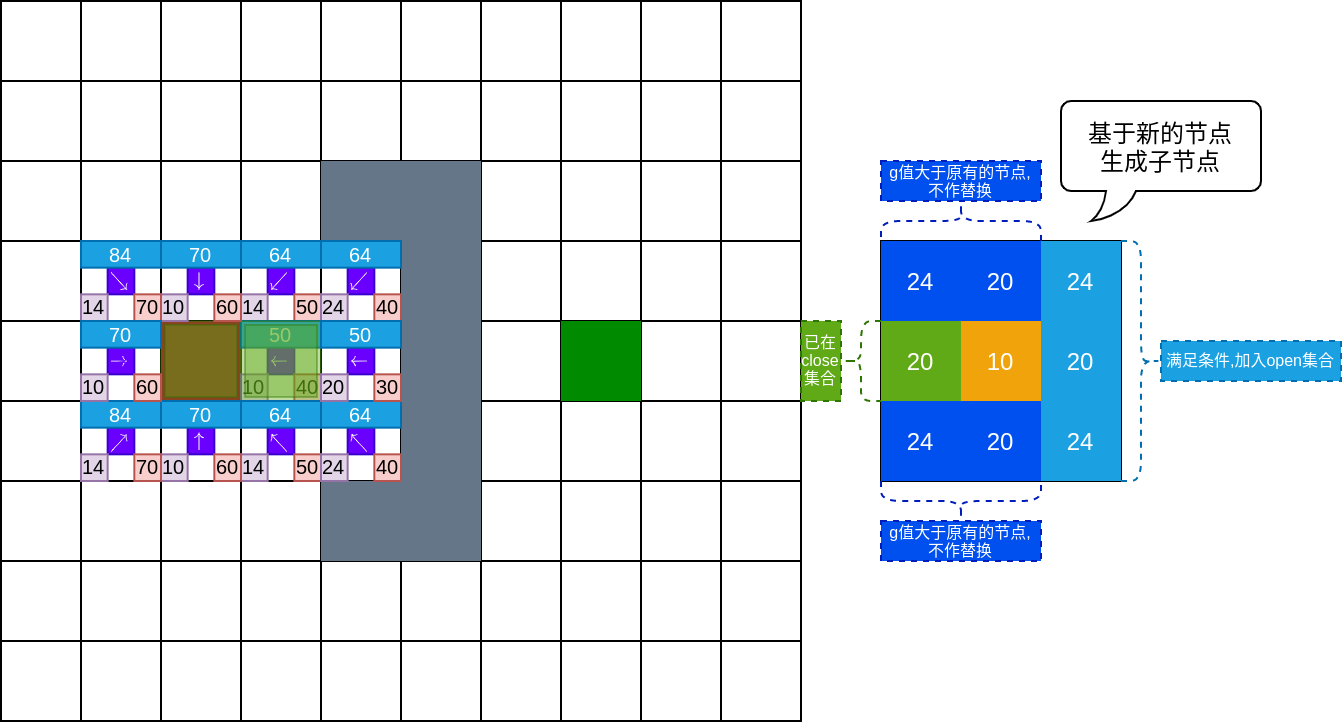
基于扩展规则,不断推出总代价值最小的节点,并扩展这些节点.下图中,当前节点右侧三个新节点与障碍存在碰撞,所以直接跳过.
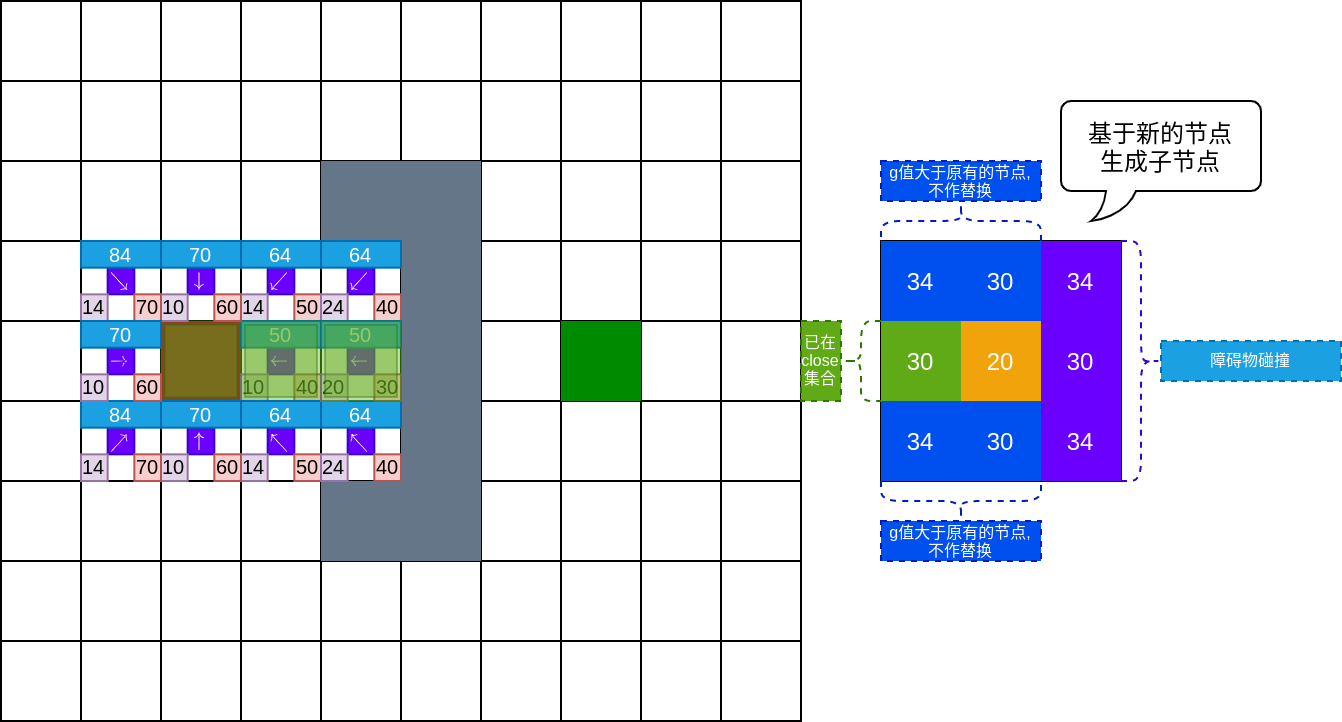
如下图所示,如果存在总代价相等的情况,则先推出最新推入的节点.下图中,假设右下方总代价值为64的节点是新推进open集合的节点.
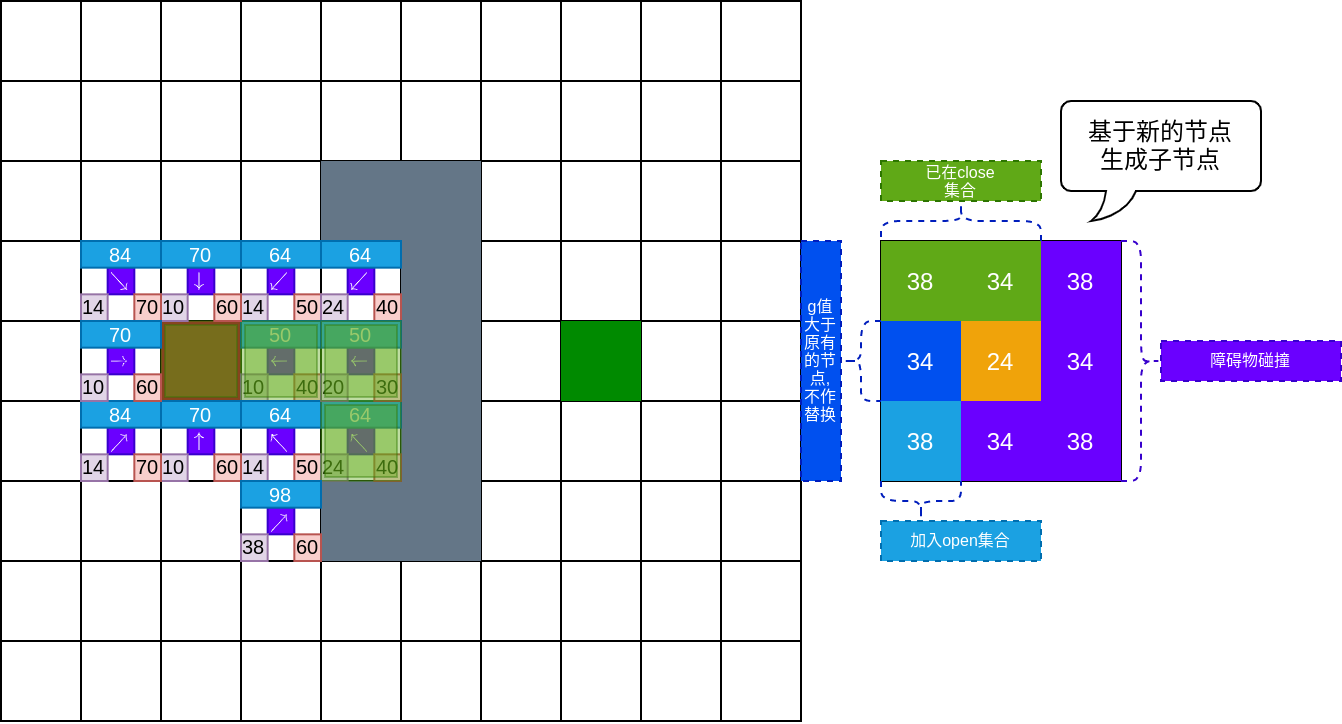
如下图所示,继续推出新的节点,并迭代更新.
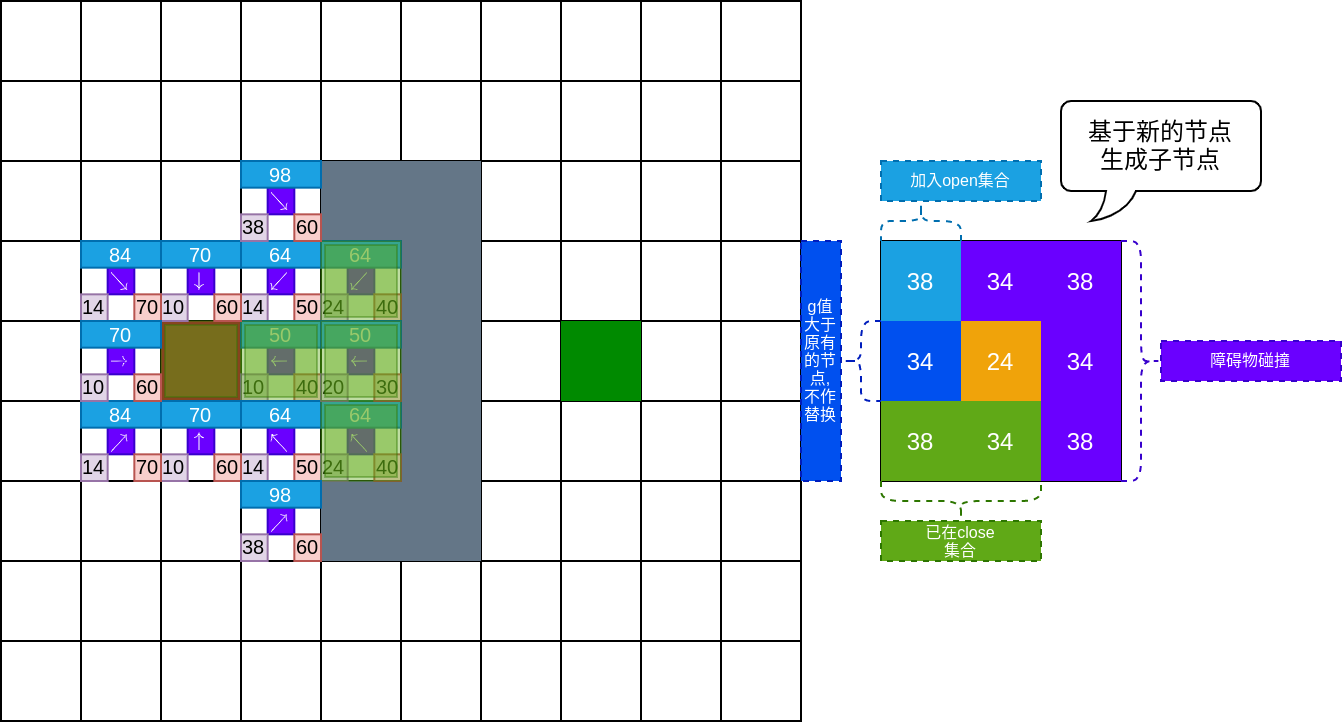
如下图所示,新的节点有的与障碍物存在碰撞,有的已经在close集合中,有的移动代价大于原先的节点;但当前节点下方的节点,其移动代价小于open集中对应节点的代价,所以需替换open集合中该节点的移动代价,并将其父节点指向当前节点.
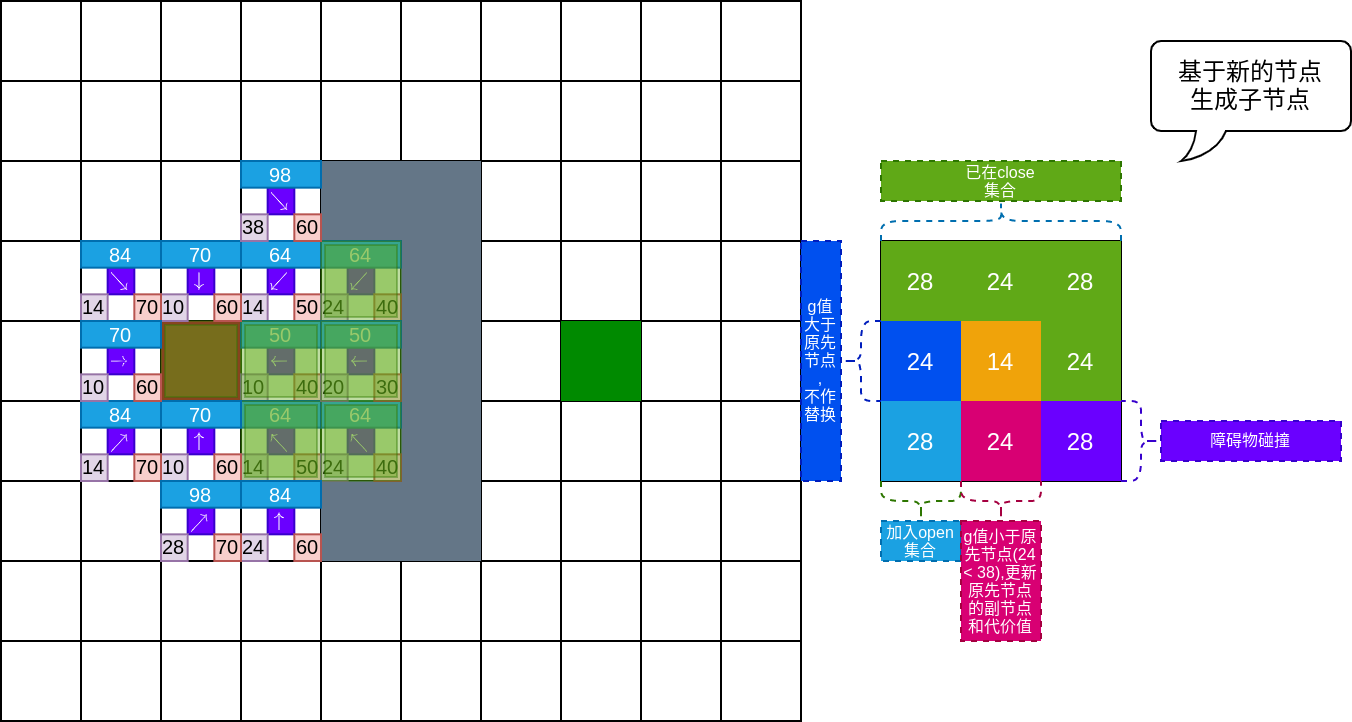
迭代
如下图所示,直到从open集合中推出的节点是终点,表明搜索结束.浅绿色蒙板包含的区域属于close集合,其它搜索过的节点属于open集合.如果遍历所有open集合的节点都无法到达终点,则搜索失败.
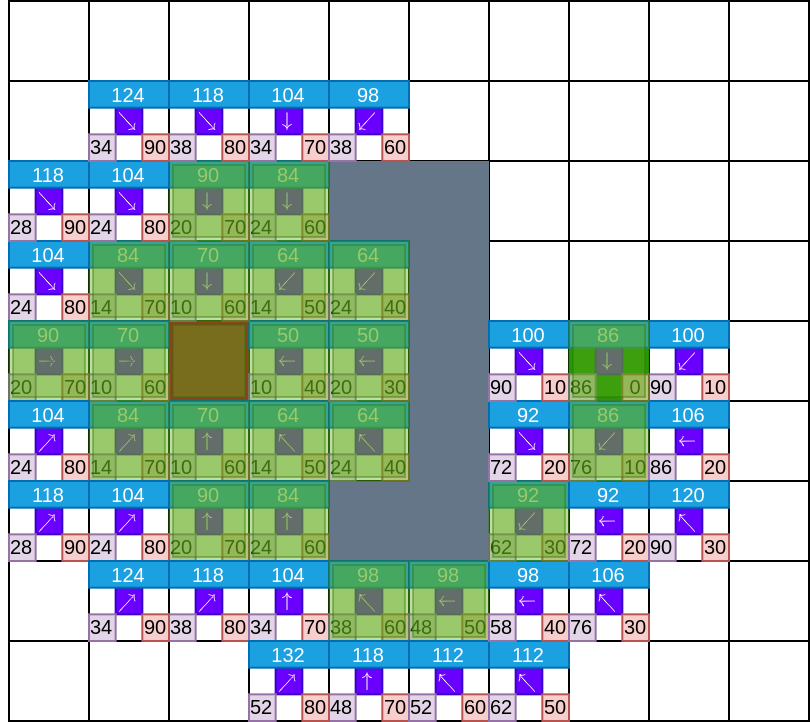
获取路径
如下图所示,搜索结束后,以终点为起始节点,根据节点所指向的父节点,反向更新搜索路径,直到节点的父节点指向为空,即到达起始点.
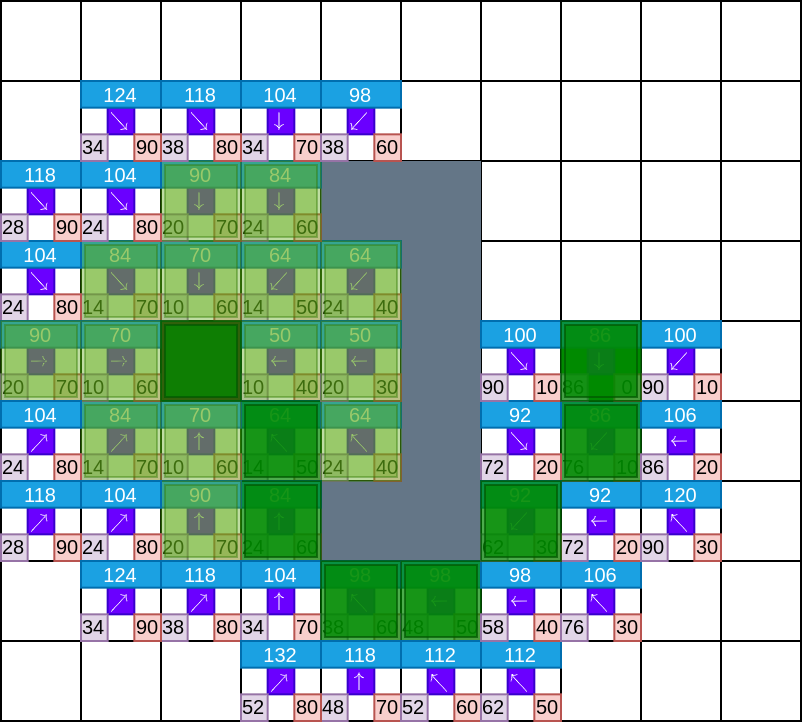
参考
- Introduction to the A* Algorithm
- Implementation of A*
- 路径规划中的Hybrid A*算法