K-Quant
Overview
在llama.cpp中,常用的量化方式为 K-Quant ,这是一种混合量化方式,即不同的模型类型和权重位置会采用不同的量化位宽。其核心思想是,对于对模型精度影响较大的权重,采用更高的量化位宽。本节重点探讨了其量化算法背后的数学原理,旨在从数学角度深入理解其背后的数学原理。
K-Quant Compare
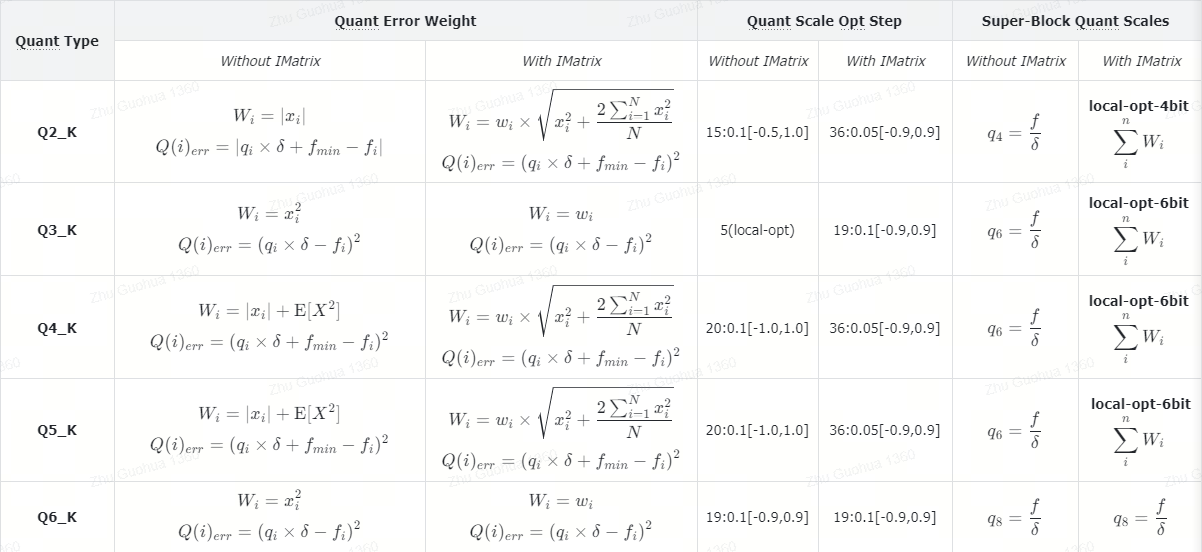
根据模型量化时是否使用IMatrix,K-Quant 算法会调用不同的实现,详细的对比如下:
Data Block Split
K-Quant 采用逐块量化的方式,首先从原始权重数据中取出256个元素作为一个量化Block,然后再将其分割为8个Super-Block,每个Super-Block包含32个待量化的权重数据。
- \(N\):表示
Block的大小; - \(n\):表示
Super-Block的大小;
IMatrix
K-Quant 支持使用i-matrix进一步提升量化精度,其核心思想是利用激活值 (activations) 的统计信息来指导权重(weights)量化。通常的量化方法可能会忽略激活值的影响,该方法试图根据激活值的重要性来调整量化系数,从而使得量化的最终目标(量化误差最小)达到最优。 对于i-matrix概念的理解,重点在于Importance单词,表示对量化精度影响比较重要的权重。当量化时,准备一份校准数据集,通过前向推理收集网络每层的激活值信息。然后根据这些激活值的分布,计算出权重对于量化目标的敏感度,哪些更重要,哪些不那么重要。
Importance Matrix Calculation
如何计算出 i-matrix,其背后的数学原理推理如下:
假设网络某一层的权重向量表示为:
\[ W_{m\times n}= \begin{bmatrix} w_{1,1} & w_{1,2} & ... & w_{1,n}\\ w_{2,1} & w_{2,2} & ... & w_{2,n}\\ ... & ... & ... & ...\\ w_{m,1} & w_{m,2} & ... & w_{m,n}\\ \end{bmatrix} \]
其中, \(m\)表示行, \(n\)表示列,则第 \(i\) 行的权重向量为
\[ W_{i,:}=\mathbf{w}_i^T = \begin{bmatrix} w_{i,1} &w_{i,2}&...&w_{i,n} \end{bmatrix} \]
假设网络某一层的激活输入为
\[ X_{n\times k}= \begin{bmatrix} x_{1,1} & x_{1,2} & ... & x_{1,k}\\ x_{2,1} & x_{2,2} & ... & x_{2,k}\\ ... & ... & ... & ...\\ x_{n,1} & x_{n,2} & ... & x_{n,k}\\ \end{bmatrix} \]
其中, \(n\) 表示行, \(k\) 表示列,则第 \(j\) 列的激活向量为:
\[ X_{:,j}=\mathbf{x}_j= \begin{bmatrix} x_{1,j}\\ x_{2,j}\\ ...\\ x_{n,j} \end{bmatrix}=(x_{1,j},x_{2,j},...,x_{n,j}) \]
那么神经网络层中的一个输出可以表示为权重向量 \(\mathbf{w}\) 和激活向量 \(\mathbf{x}\) 的点积:
\[y=\mathbf{w}_i^T\cdot \mathbf{x}_j=\sum_{t=1}^n w_{i,t}*x_{t,j}\tag{1}\]
假设权重向量 \(\mathbf{w}\) 的量化形式表示为
\[ \mathbf{q}_i^T = \begin{bmatrix} q_{i,1} &q_{i,2}&...&q_{i,n} \end{bmatrix} \]
权重量化后的输出可以表示为
\[y_q=\mathbf{q}_i^T\cdot \mathbf{x}_j=\sum_{t=1}^n q_{i,t}*x_{t,j} \tag{2}\]
最终量化目标是使量化后的权重 q 和原始权重 w 与激活向量 \(a\) 的点积结果尽量接近,即最小化量化引入的误差,以最小化RMSE为目标函数表示如下:
\[\mathtt{min} \quad |y_q-y|^2\]
结合公式(1)和(2)得,误差函数可以表示如下:
\[F_{i,j}=\Bigg[\sum_{t=1}^n(q_{i,t}-w_{i,t})x_{t,j}\Bigg]^2 \tag{3}\]
定义每个元素的量化误差为 \(r_{i,t}=q_{i,t}-w_{i,t}\) ,则
\[F_{i,j}=\Bigg[\sum_{t=1}^n r_{i,t}x_{t,j}\Bigg]^2 \tag{4}\]
由于上述公式(4)只考虑了第 \(i\) 行权重和第 \(j\) 列激活值引起的量化误差,故可以考虑整个网络的误差表示为
\[ F=\begin{bmatrix} F_{1,1} & F_{1,2} &... &F_{1,k}\\ F_{2,1} & F_{2,2} &... &F_{2,k}\\ ... & ... & ... & ...\\ F_{m,1} & F_{m,2} &... &F_{m,k}\\ \end{bmatrix} \tag{5} \]
等效于将 \(F\) 的期望值 \(\mathbf{E}[F]\) 作为量化目标:
\[\large \mathbf{E}[F]=\mathbf{E}\Bigg[\Big(\sum_{t=1}^nx_tr_t\Big)^2\Bigg]\tag{6}\]
假设 \(g = \sum_i^3x_i=x_1 + x_2 + x_3\) 则: \[\begin{align} g^2 &= \Big(\sum_i^3x_i\Big)^2\\ &= (x_1 + x_2 + x_3)(x_1 + x_2 + x_3)\\ &=x_1(x_1 + x_2 + x_3)+x_2(x_1 + x_2 + x_3)+x_3(x_1 + x_2 + x_3)\\ &=\sum_i^3\sum_j^3x_ix_j \end{align} \tag{7}\]
结合上述Tips,将表达式(6)展开得
\[ \begin{align} \mathbf{E}\Bigg[\Big(\sum_{t=1}^nx_tr_t\Big)^2\Bigg] &=\mathbf{E}\Bigg[ \Big(\sum_{t=1}^nx_tr_t\Big)\Big(\sum_{s=1}^nx_sr_s\Big)\Bigg]\\ &=\mathbf{E}\Bigg[ \sum_{t=1}^n\sum_{s=1}^n(x_tr_t)(x_sr_s)\Bigg]\\ &=\mathbf{E}\Bigg[ \sum_{t=1}^n\sum_{s=1}^n(r_tr_s)(x_tx_s)\Bigg]\\ \end{align} \tag{8} \]
由于量化误差 \(r\) 由权重量化过程确定,与输入激活 \(x\) 无关,可以将 \(r\) 移出期望运算符,故公式(8)可进一步化简得
\[ \large\mathbf{E}[F]=\mathbf{E}\Bigg[ \sum_{t=1}^n\sum_{s=1}^n(r_tr_s)(x_tx_s)\Bigg]=\sum_{t=1}^n\sum_{s=1}^n(r_tr_s)\mathbf{E}(x_tx_s) \tag{9}\]
公式(9)中出现了 \(\mathbf{E}(x_tx_s)\) 项,表示输入激活 \(\mathbf{x}_j\) 中第 \(t\) 个元素和第 \(s\) 个元素的协方差,可以定义矩阵 \(\mathbf{I}\)为:
\[\mathbf{I}= \begin{bmatrix} \mathbf{E}(x_1x_1) & \mathbf{E}(x_1x_2) & ... & \mathbf{E}(x_1x_n)\\ \mathbf{E}(x_2x_1) & \mathbf{E}(x_2x_2) & ... & \mathbf{E}(x_2x_n)\\ ... & ... & ... & ...\\ \mathbf{E}(x_nx_1) & \mathbf{E}(x_nx_2) & ... & \mathbf{E}(x_nx_n)\\ \end{bmatrix} \tag{10}\]
其中的某个元素可以表示为:
\[\mathbf{I}_{t,s}=\mathbf{E}(x_tx_s)\]
将期望符号转换为求和符号得
\[\mathbf{I}_{t,s}=\frac{1}{k}\sum_{j=1}^{k}x_{t,j}x_{s,j}\]
则矩阵 \(\mathbf{I}\) 的计算可以表示为
\[\mathbf{I}=\frac{1}{k}\sum_{j=1}^{k}\mathbf{x}_j\mathbf{x}_j^T=\frac{1}{k}\mathbf{X}\mathbf{X}^T\]
其中,\(\mathbf{x}_j= \begin{bmatrix} x_{1,j}\\ x_{2,j}\\ ...\\ x_{n,j} \end{bmatrix}\) 。在实际计算中,通常会忽略归一化因子 \(\frac{1}{k}\)。
将公式(9)拆分为对角元素和非对角元素两部分得
\[\large\mathbf{E}[F]=\sum_{i=j}\mathbf{E}[x_j^2]r_j^2+\sum_{i\neq j}\mathbf{E}[x_ix_j]r_ir_j \tag{11}\]
由于激活值的正负性以及非对角元素的激活值之间相关性较弱,故非对角线元素 \(\mathbf{E}[x_{i}x_{j}]\) 的期望值通常远小于对角线元素 \(\mathbf{E}[x_j^2]\) ,即
\[\mathbf{E}[x_ix_j] \lll \mathbf{E}[x_j^2]\]
因此可以忽略非对角线元素,简化计算,只关注对角线元素,即激活值的平方期望 \(\mathbf{E}[x_j^2]\) ,故公式(11)忽略非对角线项得
\[\large\mathbf{E}[F]\approx \sum_{i=j}\mathbf{E}[x_j^2]r_j^2\]
i-Matrix可以用于指导权重量化
因此,最小化权重的 \(\sum_{i=j}\mathbf{E}[x_i^2](q_i-\mathtt{w}_i)^2\) 等效于最小化 \(\mathbf{E}[F]\) ,表达式 \(\mathbf{E}[x_i^2]\) 可以作为 Importance Matrix 去指导量化 \(\mathtt{w}\) 权重矩阵。当 \(\mathbf{E}[x_i^2]\) 激活项较大时,需要减少对应的量化误差 \(r_i^2\), 也就是该权重要重点量化,这样才能保证目标函数 \(\mathbf{E}[F]\) CBN XF。
代码示例
在llama.cpp中计算 imatrix 矩阵的计算代码如下:
1 | for (int row = 0; row < (int)src1->ne[1]; ++row) { |
Without IMatrix
Data Weight Calculate
- 数据块(局部)幅度
首先计算权重数据块的局部(32)的平均幅度,即数据块的均方根(Root Mean Square-RMS),公式如下: \[\mathbf{E}[X^2]=\sqrt\frac{\sum_{i=1}^{n}x_i^2}{n}\] 这部分是块内所有数据点共享的,反映了整个数据块的平均能量水平。如果一个数据块的 av_x 很大,那么这个块内的所有数据点都会获得一个较高的基础权重。
- 数据点幅度
通过计算当前数据点的绝对值,获得每个数据个体的幅度值,用于反应数据本身的大小,公式如下: \[|x_i|\] 这部分是每个数据独有的,反映了该数据点自身的绝对大小。绝对值越大的数据点,会获得额外的权重。
- 数据点权重计算
每个数据点的权重为数据块幅度和数据点幅度两部分之和,最终的权重计算如下: \[W_i=|x_i|+\mathbf{E}[X^2]\] 在后续的量化优化过程中,具有以下特点的数据,其量化误差将会被赋予更高的权重(更重要):
- 位于“幅度较高”的局部邻域内的数据点:如果一个数据点周围的其他数据点的幅度也较大(导致较高的数据块幅度),那么即使它自身的幅度不是特别大,也会获得较高的权重。这可以理解为,在一个重要的局部区域内,所有数据点都应该被更精确地量化。
- 自身幅度较大的数据点:无论其周围邻域的能量如何,幅度较大的数据点本身就会获得较高的权重。这符合直觉,因为较大的数值的量化误差对整体的影响通常更大,因此需要更精确的表示。
With IMatrix
Data Weight Calculate
- 数据块峰值幅度
首先计算整个数据块(256)的平均幅度,即数据块的均方值(Mean Square-MS),或者叫峰值幅度,公式如下: \[\frac{2\sum_{i=1}^{N}x_i^2}{N}\] 其中, \(N=256\)表示整个 Block 的大小。
- 数据点幅度
通过计算当前数据点的绝对值,获得每个数据个体的幅度值,用于反应数据本身的大小,公式如下: \[x_i^2\] 这部分是每个数据独有的,反映了该数据点自身的绝对大小。绝对值越大的数据点,会获得额外的权重。
- 数据点权重计算
每个数据点的权重为数据块幅度和数据点幅度两部分之和,最终的权重计算如下: \[W_i=w_i\times \sqrt{x_i^2+\frac{2\sum_{i=1}^{N}x_i^2}{N}}\] 其中, \(w_i\)表示imatrix中的权重。
Super Block Quant
Asymmetric Quant and Dequant
根据数据分布范围,找出其中的最大值和最小值,然后根据量化的bit数(例如4bit),按照如下公式计算量化的缩放系数: \[\delta=\frac{f_{max}-f_{min}}{2^{bit}-1}=\frac{f_{max}-f_{min}}{15}\]
如下图所示,是4bit非对称量化的示意图,显示了浮点数值分布与量化数值分布的关系:

量化表示如下:
\[q=\frac{f-f_{min}}{\delta}\]
反量化表示如下:
\[f = q\times\delta+ f_{min}\]
Symmetric Quant and Dequant
如果是对称量化,计算比较简单,直接找出数据分布的最大值,然后根据量化bit位宽,按照如下公式计算量化系数:
\[\delta=\frac{|f|_{max}}{-2^{(bit-1)}}\] 其中, \[|f|_{max}= \begin{cases} f_{max} &\text{if } |f_{max}|>|f_{min}| \\ f_{min} &\text{if } |f_{max}|<|f_{min}| \end{cases}\]
如下图所示,是6bit对称量化的示例图,根据绝对值最大的值是负数还是正数,采取不同的映射策略:
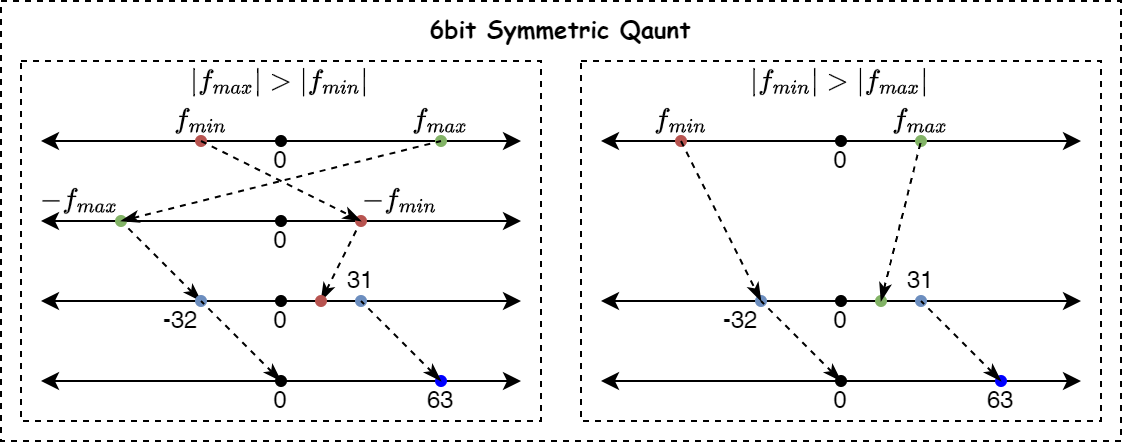
量化表示如下:
\[q=\frac{f}{\delta}\]
反量化表示如下:
\[f = q\times\delta\]
Quant Optimization
根据采用的量化算法的对称方式,可以分为对称和非对称两种方式,它们详细的量化误差表示略有不同,下面根据不同量化对称方式分析其量化算法的数学原理。
Asymmetric
如下图所示,是目前llama.cpp采用非对称量化算法的数据结构示意图,主要分析了Block内的浮点和量化数据是如何在内存中排布的。其中图的左边表示浮点数据的排布,右边的qs或qh表示量化数据的排布。
- Q2_K
如下图所示,是 Q2_K 量化算法的数据存储示意图。整个 Block 的量化系数和零点值以float16格式存储,占据4字节的空间。然后再将整个浮点数据块 Block 划分为16个 Super-Block ,每个 Super-Block 拥有自己的量化系数和零点值,且各自的数据位宽为4bit,正好拼接为1byte存储,高4bit表示零点值,低4bit位表示量化系数,一共占据16个字节空间。其中,红色的Block0和Block1占据整个32个量化qs的最低2bit,其它Block按照图中规律存储。
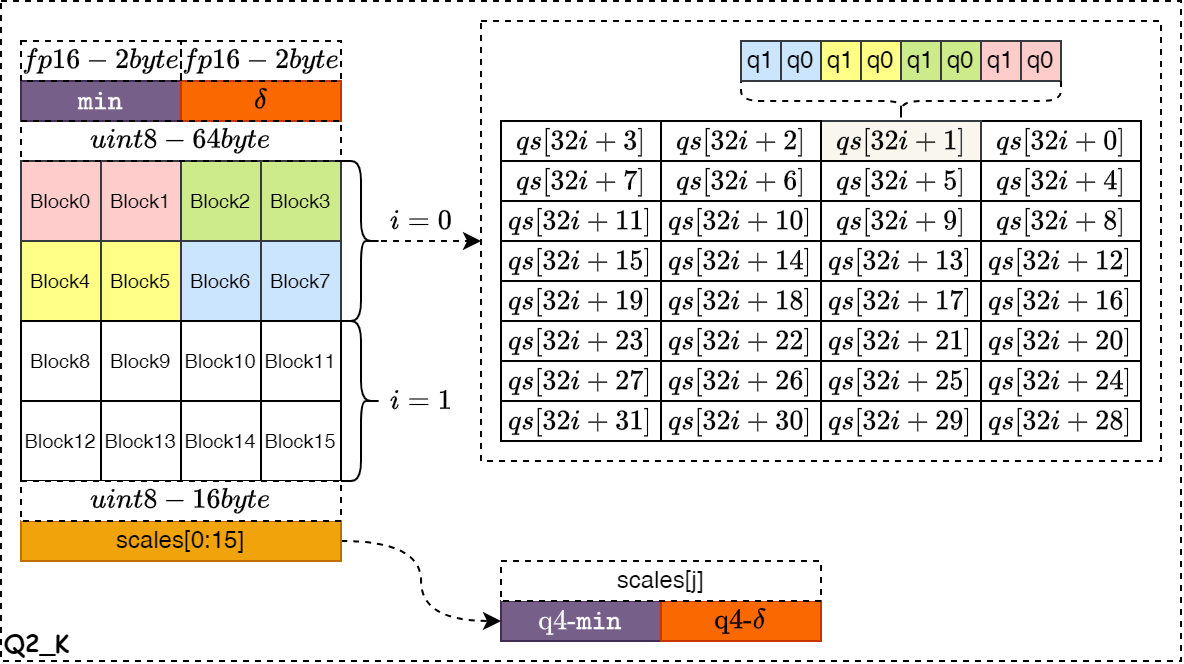
- Q4_K
如下图所示,是 Q4_K 量化算法的数据存储示意图。整个Block 的量化系数和零点值以float16格式存储,占据4字节的空间。然后再将整个浮点数据块 Block 划分为8个 Super-Block ,每个 Super-Block 拥有自己的量化系数和零点值,且数据位宽为6bit,按照图中的结构进行拼接,一共占据12个字节空间。每两个 Super-Block 进行拼接,分别占据每个qs对象的高和低4bit,并使用一个32字节的数组保存,一共4个组共128字节。
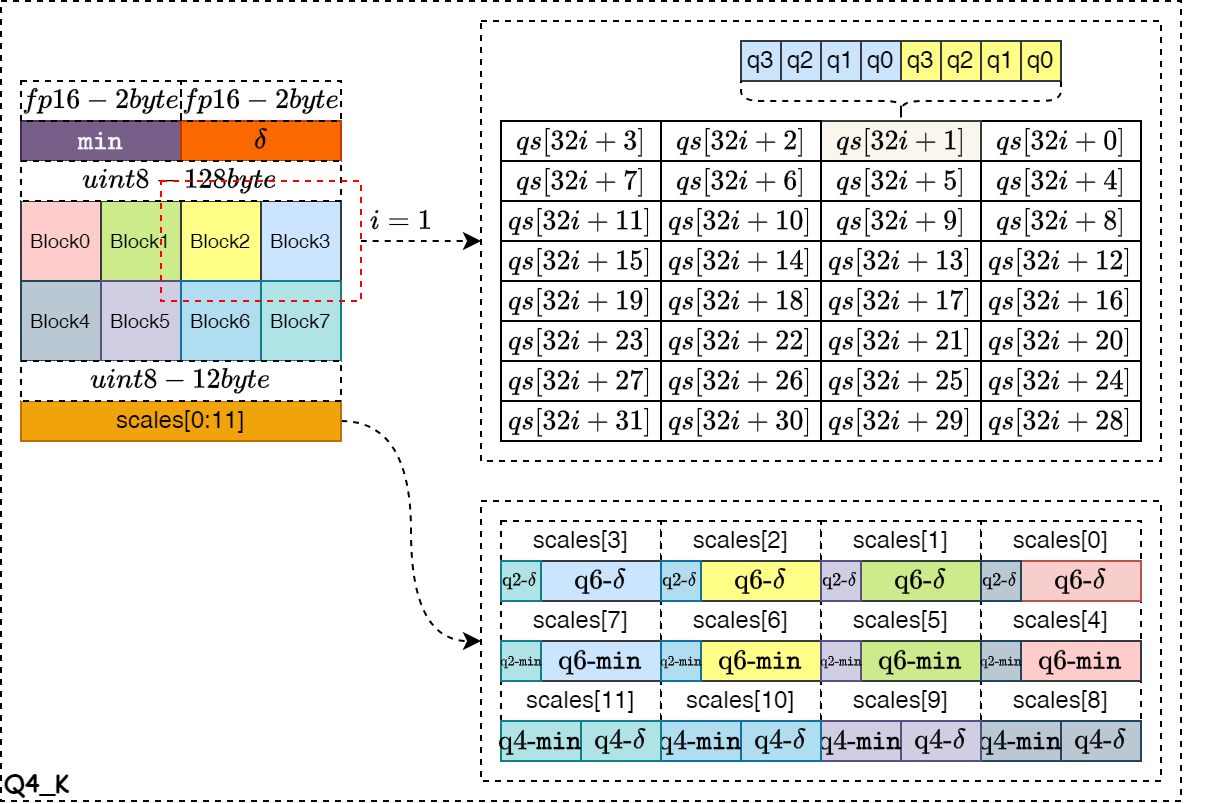
- Q5_k
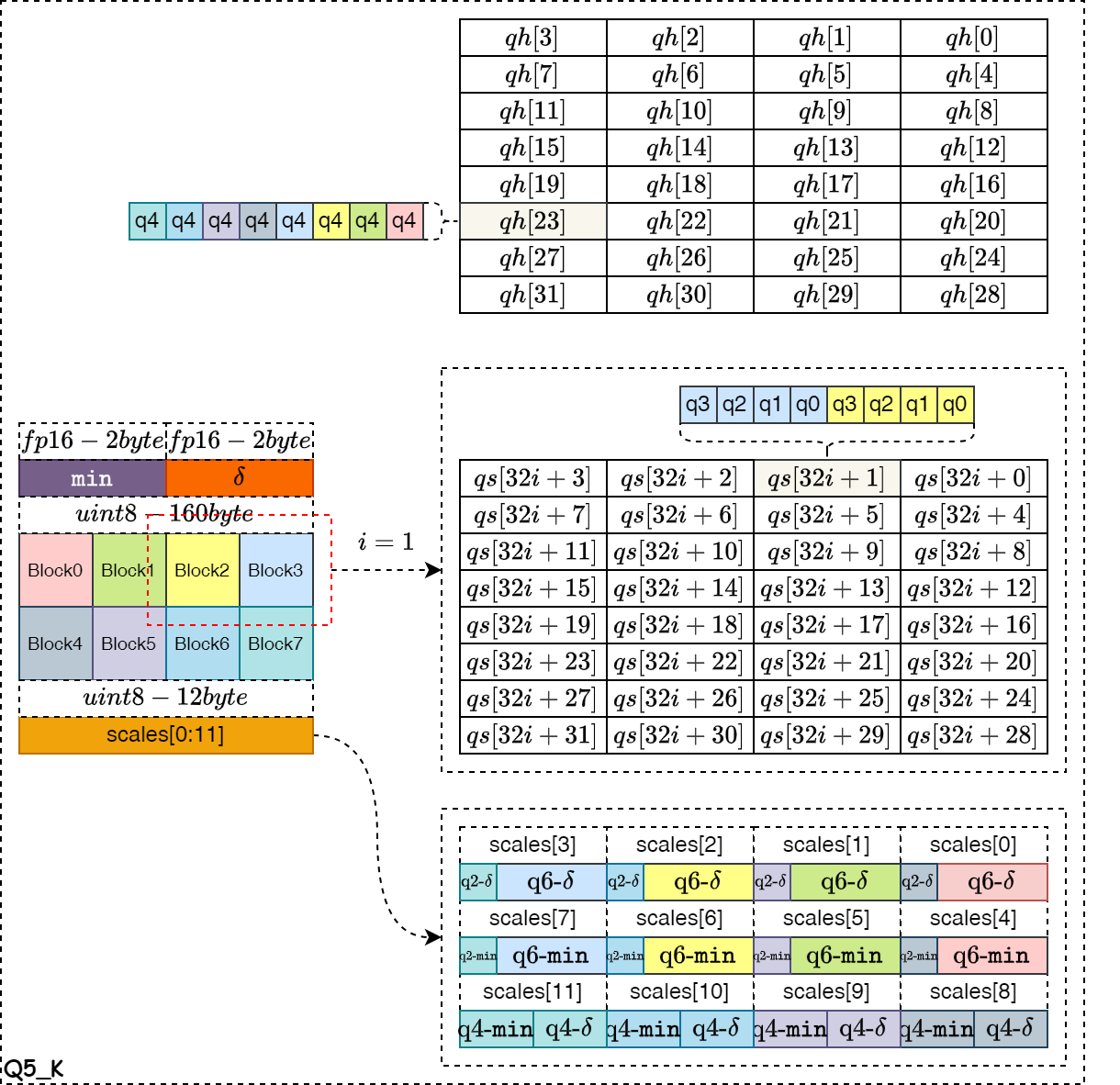
如下图所示,是 Q5_K 量化算法的数据存储示意图。整个 Block 的量化系数和零点值以float16格式存储,占据4字节的空间。然后再将 Block 划分为8个 Super-Block ,每个 Super-Block 拥有自己的量化系数和零点值,且数据位宽为6bit,按照图中的结构进行拼接,一共占据12个字节空间。每两个 Super-Block 的低4bit位进行合并,组成一个32字节的qs数组。这8个Super-Block的第5个bit拼接为一个字节,使用一个32字节的qh数组保存,一共160字节。
Quant Error
为了最小化整个数据块的量化误差,可以将某个数据的量化误差表示为: \[Q(i)_{err}=|q_{i}\times\delta+ f_{min}-f_i|\] 或者 \[Q(i)_{err}=(q_{i}\times\delta+ f_{min}-f_i)^2\] 则整个Super-Block内的量化误差表示为: \[Q_{err}=\sum_{i=1}^{n}Q(i)_{err}\] 由于每个数据对量化误差的敏感度不一,则将考虑了误差权重的表达式表示如下: \[Q_{err}=\sum_{i=1}^{n}W_{i}\times Q(i)_{err}\]
Quant-Scale OPT
为了最小化Super-Block内的量化误差之和,则设定优化目标可以表示为:
\[\mathbf{argmin}_{\delta,f_{min}} \quad Q_{err}=\sum_{i=1}^{n}W_i \times (q_{i}\times\delta+ f_{min}-f_i)^2\]
可以通过求解最小二乘问题,求得优化的 \(\delta\)和 \(f_{min}\)。
- 对 \(\delta\)求偏导,并令等式为
0得: \[\sum_{i=1}^{n}W_i \times (q_{i}\times\delta+ f_{min}-f_i)q_i=0\] 上式展开得 \[\delta\sum_{i=1}^{n}W_{i}\times q_{i}^2 +f_{min}\sum_{i=1}^{n}W_iq_i=\sum_{i=1}^{n}W_{i}f_iq_i \tag{1}\] - 对 \(f_{min}\)求偏导,并令等式为
0得: \[\sum_{i=1}^{n}W_i \times (q_{i}\times\delta+ f_{min}-f_i)=0\] 上式展开得 \[\delta\sum_{i=1}^{n}W_{i}\times q_{i} +f_{min}\sum_{i=1}^{n}W_i=\sum_{i=1}^{n}W_{i}f_i \tag{2}\] 故结合上述等式(1)和(2),可以得到两个关于 \(\delta\)和 \(f_{min}\)的线性方程组: \[ \begin{align} \delta\sum_{i=1}^{n}W_{i}\times q_{i}^2 +f_{min}\sum_{i=1}^{n}W_iq_i &=\sum_{i=1}^{n}W_{i}f_iq_i\\ \delta\sum_{i=1}^{n}W_{i}\times q_{i}+f_{min}\sum_{i=1}^{n}W_i& =\sum_{i=1}^{n}W_{i}f_i \end{align} \tag{3} \] 将等式(3)使用矩阵形式表示如下: \[ \Large \begin{bmatrix} \sum_{i=1}^{n}W_{i}q_{i}^2 & \sum_{i=1}^{n}W_iq_i \\ \sum_{i=1}^{n}W_{i}q_{i} & \sum_{i=1}^{n}W_i \end{bmatrix} \begin{bmatrix} \delta\\ f_{min} \end{bmatrix}= \begin{bmatrix} \sum_{i=1}^{n}W_{i}f_iq_i\\ \sum_{i=1}^{n}W_{i}f_i \end{bmatrix} \tag{4} \]
克莱姆法则: 假设多项式表示如下: \[ \begin{array}{cc} ax+by&=\textcolor{red}{e}\\ cx+dy&=\textcolor{red}{f} \end{array} \] 使用矩阵来表示为: \[ \begin{bmatrix} a & b\\ c & d \end{bmatrix} \begin{bmatrix} x\\y \end{bmatrix}= \begin{bmatrix} \textcolor{red}{e}\\\textcolor{red}{f} \end{bmatrix} \] 当矩阵可逆时,x和y可以从克莱姆法则中得出: \[ x=\frac{ \begin{vmatrix} \textcolor{red}{e} & b\\ \textcolor{red}{f} & d \end{vmatrix} }{ \begin{vmatrix} a & b\\ c & d \end{vmatrix} }=\frac{\textcolor{red}{e}d-b\textcolor{red}{f}}{ad-bc} \] 同时 \[ y=\frac{ \begin{vmatrix} a&\textcolor{red}{e}\\ c&\textcolor{red}{f} \end{vmatrix} }{ \begin{vmatrix} a & b\\ c & d \end{vmatrix} }=\frac{a\textcolor{red}{f}-\textcolor{red}{e}c}{ad-bc} \] 假设使用 \(\mathbf{A}= \begin{bmatrix} a & b\\ c & d \end{bmatrix}\)表示线性矩阵,则行列式表示为\(\det(\mathbf{A})=\begin{vmatrix} a & b\\ c & d \end{vmatrix}\)
- 可解性判据: \(\det(\mathbf{A})\) 是用于判断上述线性方程组是否存在唯一解的关键。
- 如果 \(\det(\mathbf{A})>0\) ,则方程组有唯一解,意味着我们可以找到一组唯一的 \(\delta\) 和 \(f_{min}\) 来最小化误差。
- 如果 \(\det(\mathbf{A})=0\),则方程组无解或有无穷多解,这意味着我们无法找到唯一的 \(\delta\) 和 \(f_{min}\) 来最优地拟合数据。这通常发生在 的所有值都相等或存在线性依赖关系的情况下。
- 如果 \(\det(\mathbf{A})<0\),在实数域中通常不会出现这种情况,因为 \(ad \ge bc\)(这可以从柯西-施瓦茨不等式推导出来)。
根据克莱姆法则,最优的 \(\delta\)可以表示为: \[\delta=\frac{ \begin{vmatrix} \textcolor{red}{\sum_{i=1}^{n}W_{i}f_iq_i} & \sum_{i=1}^{n}W_iq_i\\ \textcolor{red}{\sum_{i=1}^{n}W_{i}f_i} & \sum_{i=1}^{n}W_i \end{vmatrix} }{ \begin{vmatrix} \sum_{i=1}^{n}W_{i}q_{i}^2 & \sum_{i=1}^{n}W_iq_i \\ \sum_{i=1}^{n}W_{i}q_{i} & \sum_{i=1}^{n}W_i \end{vmatrix} }=\frac{ \textcolor{red}{\sum_{i=1}^{n}W_{i}f_iq_i} \times \sum_{i=1}^{n}W_i-\sum_{i=1}^{n}W_iq_i\times \textcolor{red}{\sum_{i=1}^{n}W_{i}f_i} }{\sum_{i=1}^{n}W_{i}q_{i}^2\times \sum_{i=1}^{n}W_i-\sum_{i=1}^{n}W_iq_i\times \sum_{i=1}^{n}W_iq_i} \tag{5}\] 同理,最优的 \(f_{min}\)可以表示为 \[f_{min}=\frac{ \begin{vmatrix} \sum_{i=1}^{n}W_{i}q_{i}^2 &\textcolor{red}{\sum_{i=1}^{n}W_{i}f_iq_i}\\ \sum_{i=1}^{n}W_{i}q_{i} & \textcolor{red}{\sum_{i=1}^{n}W_{i}f_i} \end{vmatrix} }{ \begin{vmatrix} \sum_{i=1}^{n}W_{i}q_{i}^2 & \sum_{i=1}^{n}W_iq_i \\ \sum_{i=1}^{n}W_{i}q_{i} & \sum_{i=1}^{n}W_i \end{vmatrix} }=\frac{ \sum_{i=1}^{n}W_{i}q_{i}^2 \times \textcolor{red}{\sum_{i=1}^{n}W_{i}f_i}-\textcolor{red}{\sum_{i=1}^{n}W_{i}f_iq_i}\times \sum_{i=1}^{n}W_{i}q_{i} }{ \sum_{i=1}^{n}W_{i}q_{i}^2\times \sum_{i=1}^{n}W_i-\sum_{i=1}^{n}W_iq_i\times \sum_{i=1}^{n}W_iq_i } \tag{6}\] 其中,需要保证 \(\begin{vmatrix} \sum_{i=1}^{n}W_{i}q_{i}^2 & \sum_{i=1}^{n}W_iq_i \\ \sum_{i=1}^{n}W_{i}q_{i} & \sum_{i=1}^{n}W_i \end{vmatrix} > 0\)。
Quant-Scale Update
根据量化公式 \(q=\frac{f-f_{min}}{\delta}\) 知,通过动态调整量化系数 \(\delta\) 的大小,可以对数据的量化结果进行调整。
\[\set{\frac{1}{\delta_j}|\frac{(2^{bit}-1)+r_{min}+\delta_r*j}{f_{max}-f_{min}}, j \in[1,step]}\]
假设采用4bit量化, \(r_{min}=-1.0\), \(\delta_r=0.1\), \(step=20\),则
\[\set{\frac{1}{\delta_j}|\frac{15-1+0.1*j}{f_{max}-f_{min}}, j \in[1,20]}\]
从而得到一组新的量化数值 \(\set{q_i|i\in[1,n]}\) ,根据量化的最优目标 \(\mathtt{minimine} \quad Q_{err}\) ,并结合公式(5)和(6)可以得到新的量化系数 \(\delta_{b}\) 和 \(b_{min}\),并重新计算出新的 \(Q_{err}^j=\sum_{i=1}^{n}W_i \times (q_{i}\times\delta_{b}+ b_{min}-f_i)^2\)
如果新的 \(Q_{err}^j < Q_{err}\) ,则更新 \(\delta_{b}\) 和 \(b_{min}\) 为最终输出的量化系数。
Symmetric Quant and Global Optimum(Q6_K)
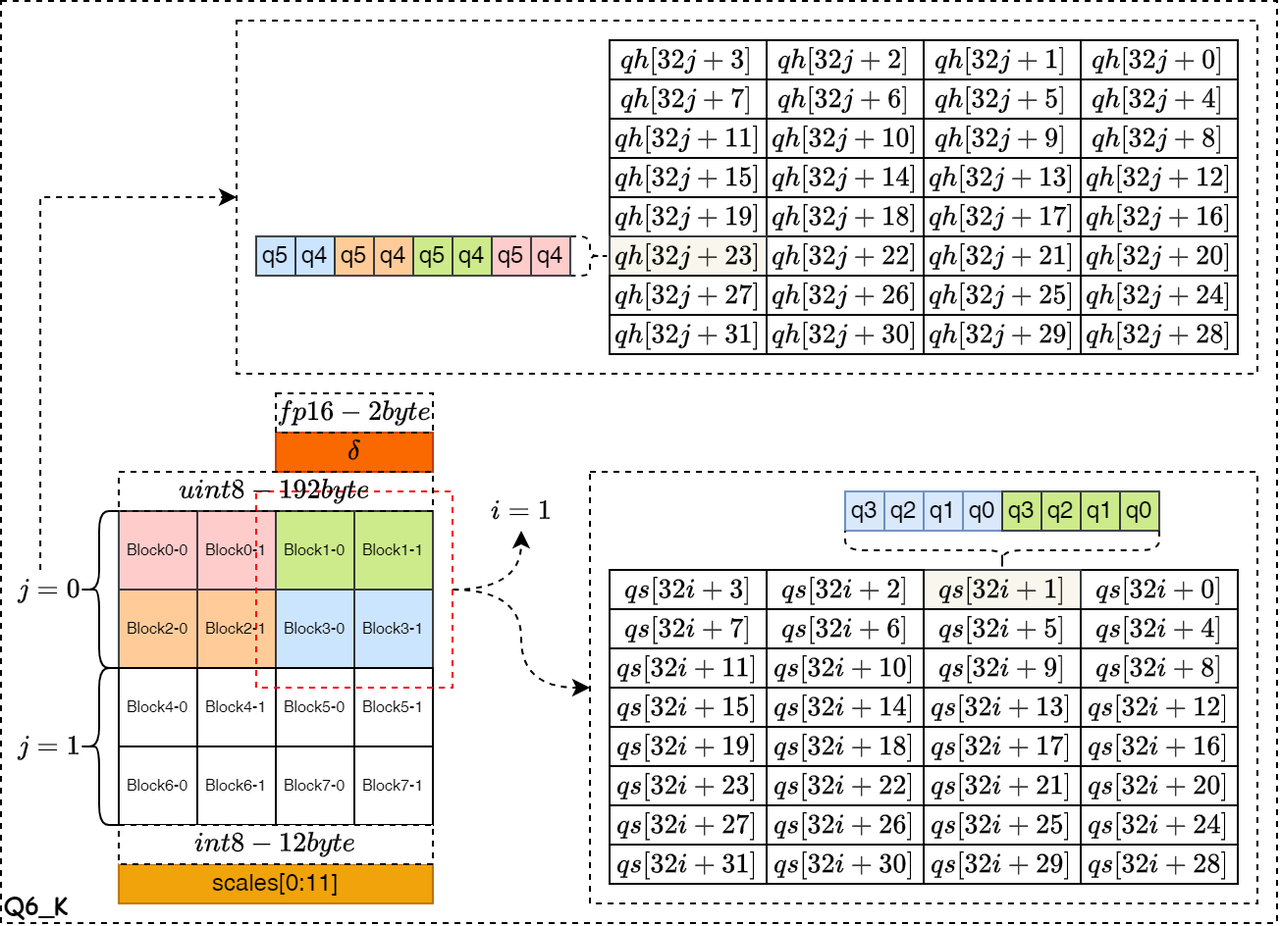
如下图所示,是对称量化算法的数据结构示意图,其中图的左边表示浮点数据的排布,右边的qs和qh表示量化数据的排布。下图是 Q6_K 量化算法的数据存储示意图,整个 Block 的量化系数以float16格式存储,占据2字节的空间。然后再将整个浮点数据块 Block 划分为16个 Super-Block ,每个 Super-Block 拥有自己的量化系数,且量化数据的位宽为6bit,一共占据12个字节空间。如图中红框标注的,Block1-0和Block1-1共同占据32个存储量化qs对象的最低4bit,Block3-0和Block3-1占据整个32个量化qs对象的最高4bit。剩余的2bit位,使用qh数组对象保存,并由相邻两个Super-Block的浮点数填满对应的2bit位。
Quant Error
为了最小化整个数据块的量化误差,可以将某个数据的量化误差表示为: \[Q(i)_{err}=|q_{i}\times\delta-f_i|\] 或者 \[Q(i)_{err}=(q_{i}\times\delta-f_i)^2\]
则整个Super-Block内的量化误差表示为:
\[Q_{err}=\sum_{i=1}^{n}Q(i)_{err}\]
由于每个数据对量化误差的敏感度不一,则考虑误差权重的表达式如下:
\[Q_{err}=\sum_{i=1}^{n}W_{i}\times Q(i)_{err}\]
Quant Scale OPT
为了最小化Super-Block内的量化误差之和,则设定优化目标可以表示为:
\[\mathbf{argmin}_{\delta} \quad Q_{err}=\sum_{i=1}^{n}W_i \times (q_{i}\times\delta-f_i)^2\]
可以通过求解最小二乘问题,求得优化的 \(\delta\)。
- 对 \(\delta\)求偏导,并令等式为
0得:
\[\sum_{i=1}^{n}W_i \times (q_{i}\times\delta-f_i)q_i=0\] 上式展开得 \[\delta\sum_{i=1}^{n}W_{i}q_{i}^2 =\sum_{i=1}^{n}W_{i}f_iq_i\] 求解得 \[\delta_{b}=\frac{\sum_{i=1}^{n}W_{i}f_iq_i}{\sum_{i=1}^{n}W_{i}q_{i}^2} \tag{7}\]
Quant Scale Update
根据量化公式 \(q=\frac{f}{\delta}\) 知,通过动态调整量化系数 \(\delta\) 的大小,可以对数据的量化结果进行调整。 \[\set{\frac{1}{\delta_j}|\frac{-\large(2^{bit-1}+\delta_r*j\large)}{|f|_{max}}, j \in[1,step]}\] 假设采用6bit量化, \(\delta_r=0.1\), \(step=[-9,9]\),则
\[\set{\frac{1}{\delta_j}|\frac{-(32+0.1*j)}{|f|_{max}}, j \in[-9,9]}\]
从而得到一组新的量化数值 \(\set{q_i|i\in[1,n]}\) ,根据量化的最优目标 \(\mathtt{minimine} \quad Q_{err}\) ,并结合公式(7)可以得到新的量化系数 \(\delta_{b}\) ,并重新计算出新的 \(Q_{err}^j=\sum_{i=1}^{n}W_i \times (q_{i}\times\delta_{b}-f_i)^2\) 。 \[
\begin{align}
Q_{err}^j
&=\sum_{i=1}^{n}W_i \times (q_{i}\delta_{b}-f_i)^2\\
&=\sum_{i=1}^{n}W_if_i^2 -2\sum_{i=1}^{n}W_iq_{i}\delta_{b}f_i + \sum_{i=1}^{n}W_i(q_{i}\delta_{b})^2\\
&=\textcolor{red}{\sum_{i=1}^{n}W_if_i^2}-2\delta_{b}\sum_{i=1}^{n}W_iq_{i}f_i + \delta_{b}^2\sum_{i=1}^{n}W_iq_{i}^2
\end{align}
\tag{8}
\] 其中, 因为校验集数据集在量化过程中是固定的,则 \(\sum_{i=1}^{n}W_if_i^2\) 项可以看作常数,将公式(7)计算的 \(\delta_b\) 项代入公式(8)可得 \[
\begin{align}
Q_{err}^j
&=\textcolor{red}{Constant}-2\frac{\sum_{i=1}^{n}W_{i}f_iq_i}{\sum_{i=1}^{n}W_{i}q_{i}^2}\sum_{i=1}^{n}W_iq_{i}f_i + (\frac{\sum_{i=1}^{n}W_{i}f_iq_i}{\sum_{i=1}^{n}W_{i}q_{i}^2})^2\sum_{i=1}^{n}W_iq_{i}^2\\
&=\textcolor{red}{Constant}-\frac{(\sum_{i=1}^{n}W_{i}f_iq_i)^2}{\sum_{i=1}^{n}W_{i}q_{i}^2}
\end{align}
\tag{9}
\] 故 \(\mathtt{minimine} \quad Q_{err}^j\) 等效于 \[\mathtt{maxmine} \quad \frac{(\sum_{i=1}^{n}W_{i}f_iq_i)^2}{\sum_{i=1}^{n}W_{i}q_{i}^2}\] 结合公式(7)可得 \[\mathtt{maxmine} \quad \delta_{b}\sum_{i=1}^{n}W_{i}f_iq_i\] 只要 \(\delta_{b}\sum_{i=1}^{n}W_{i}f_i\hat{q}_i > \delta\sum_{i=1}^{n}W_{i}f_iq_i\) ,则更新 \(\delta_{b}\) 为最终输出的量化系数。
Symmetric Quant and Local Optimum(Q3_K)
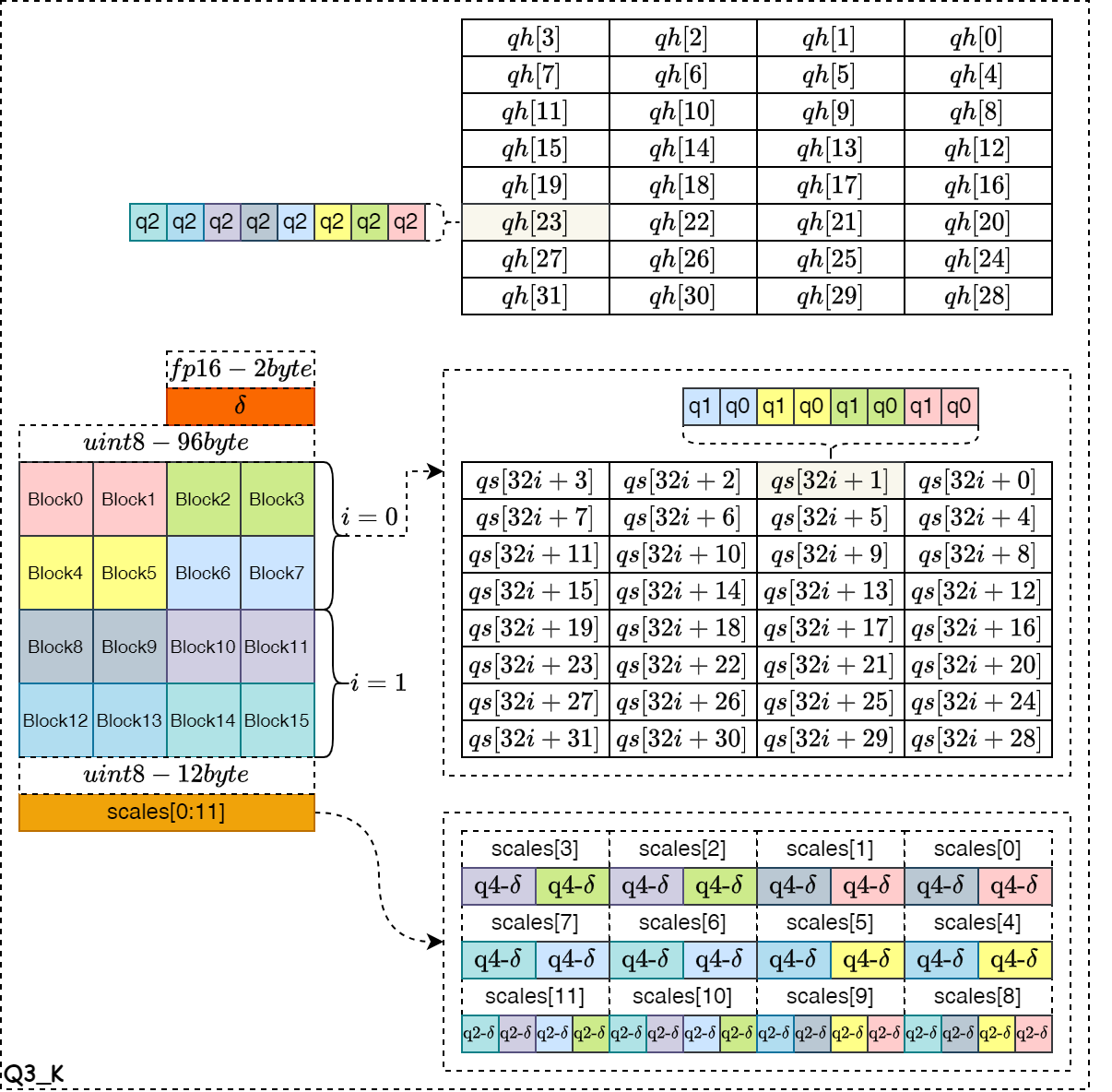
如下图所示,是对称量化算法的数据结构示意图,其中图的左边表示浮点数据的排布,右边的qs和qh表示量化数据的排布。下图是 Q3_K 量化算法的数据存储示意图,整个 Block 的量化系数以float16格式存储,占据2字节的空间。然后再将整个浮点数据块 Block 划分为16个 Super-Block ,每个 Super-Block 拥有自己的量化系数,且各自的数据位宽为6bit,一共占据12个字节空间,具体的量化系数排布如图中右下角所示。量化数值为3bit位宽,其中低2bit存储在qs对象中,高1bit存储在qh对象中。例如,Block0和Block1都对应qs数组对象的最低2bit位,Block0对应前16个qs数组对象,Block1对应后16个qs数组对象。Block0和Block1同时对应qh数组对象的最低1bit位,Block0对应前16个qh数组对象,Block1对应后16个qh数组对象。
为了最小化Super-Block内的量化误差之和,则设定RMSE优化的目标可以表示为:
\[\mathtt{minimine} \quad \sum_{i=0}^{n-1}W_i \times (q_{i}\times\delta-f_i)^2\]
可以考虑估计一个局部最优的比例因子,使得量化误差局部最优。
当关注优化单个元素 \(q_i\) 时,假设其它元素的量化值保持不变。为了决定 \(q_i\) 一个好的候选值,需要一个临时、局部的比例因子,这个比例因子在当前迭代状态下,对于除了元素 i 之外的所有元素来说是“最优”的。
- 考虑排除元素 i 后的加权平方误差:
\[Q_{err}(\delta)=\large\sum_{j!=i}^{n-1}W_j \times (q_{j}\times\delta-f_j)^2\]
目标是找到一个比例因子 \(\delta_{local}\) ,使得这个 \(Q_{err}(\delta)\) 最小。 为了找到最小值,我们可以对 \(Q_{err}(\delta)\) 关于 \(\delta_{local}\) 求导并令导数为零得 \[\large\delta_{local}=\frac{\sum_{j!=i}^{n-1}W_{j}f_jq_j}{\sum_{j!=i}^{n-1}W_{j}q_{j}^2}=\frac{\sum_{j=0}^{n-1}W_{j}f_jq_j-W_{i}f_iq_i}{\sum_{j=0}^{n-1}W_{j}q_{j}^2-W_{i}q_{i}^2}\]
当前量化状态下,排除元素 i 后剩余元素的加权平方误差最小的比例因子。
Super-Block Scale Quant
然后对每个 Super-Block 的量化系数再进行非对称或对称6bit量化,并将量化系数存储在外部的数据结构中。