CTC Loss介绍

发表于 分类于 ， 阅读次数： Changyan： Disqus：

概述

CTC，全称是Connectionist Temporal Classification，中文译为连接时序分类。特别适用于处理序列数据，例如语音识别、手写识别和机器翻译等任务，其中输入序列和输出序列的长度可能不一致。 更具体地说，CTC 解决了序列标注问题中标签与输入长度不匹配的难题。传统的序列标注方法要求输入序列和输出序列长度一致，而 CTC 允许输出序列比输入序列短，并引入了空白符（blank symbol）来处理重复和不必要的标签。

对齐问题

数据集标注时如何实现文本与语音的对齐，如下图所示，假设输入语音序列的长度为6，输出标签序列为 \(Y=[c,a,t]\)。

直接对齐
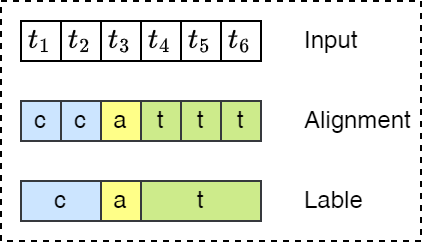
  1. 强制每个输入元素与某个输出对齐是没有意义的，例如，语音识别中，输入元素可以是没有相应输出的静音段。
  2. 无法生成连续的多个字符的输出，例如对齐 \([h,h,e,l,l,l,o,o]\)，合并重复将产生 helo 而不是 hello。

CTC对齐

为了解决上述问题，CTC 允许输出集引入一个新的标记，该标记称为 空标记(blank)。如果序列中有两个相同的字符，那么有效的对齐必须在他们之间插入一个 \(\epsilon\)，参考下图处理过程。

假设一个输入序列 \(X\) 的长度为 \(T\)，定义一个网络具有 \(m\) 维输入和 \(n\) 维输出，权重向量 \(w\) 表示为连续映射 \(\mathcal{N}_w:(\Bbb{R} ^m)^T \longmapsto (\Bbb{R} ^n)^T\)。

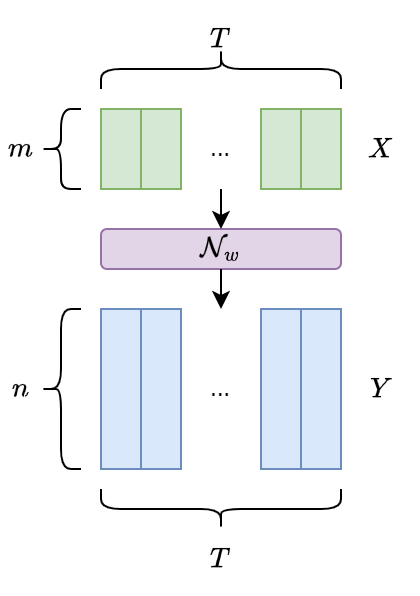
输入和输出映射关系
  1. \(L\)：序列标注任务中的标签所在字母表(汉字)集合为 \(L\)；
  2. \(L'^T\)：扩展的字母表集合，相比 \(L\) 集合多包含一个标签，记为 blank，即 \(L'=L \cup \{blank\}\) 。
  3. \(y_k^t\)：使用 \(\mathtt{y}=\mathcal{N}_w(\mathtt{x})\) 表示网络输出的序列，其中 \(y_k^t\) 表示输出单元 \(k\) 在 \(t\) 时刻的激活，可以理解为在 \(t\) 时预测为 \(L'^T\) 中的元素 \(k\) 的概率。
  4. \(L'^T\)：在集合 \(L'^T\) 上所有长度为 \(T\) 的序列集合； 假设在每一个时刻的输出与其他时刻的输出是条件独立的（或者说，条件独立于给定的 xx ），那么可以得到在给定输入 \(\mathtt{x}\) 后，得到 \(L'^T\) 集合中任何一条路径 \(\pi\) 的概率分布表示为： \[\large p(\pi|\mathtt{x})= \prod_{t=1}^{T}y_{\pi_t}^t, \forall \pi \in L'^T.\] 其中， 我们称 \(L'^T\) 中元素组成的序列 \(\pi\) 为路径(paths)，即网络输出序列中所有可能的标签组合。

由于在集合 \(L'^T\) 中可能存在多条paths，最终所映射的都是同一个标签序列，故定义多对一的函数映射 \(\mathcal{B}:L'^T \longmapsto L^{\le T}\)，其中 \(L^{\le T}\) 表示所有可能标签的集合。 例如： \[\mathcal{B}(a-ab-)=\mathcal{B}(-aa--abb)=aab\]

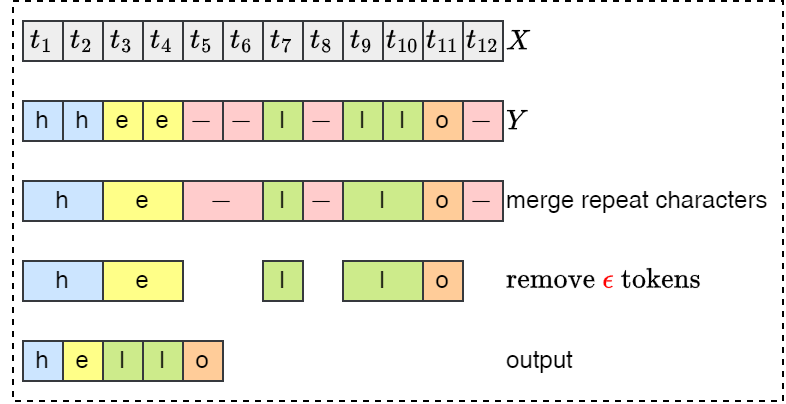
多对一函数映射示例

故给定序列 \(\mathtt{x}\) ，标签序列 \(\mathtt{l} \in L^{\le T}\) 的条件概率 \(p(\mathtt{l}|\mathtt{x})\) 表示为所有对应 \(\mathtt{l}\) 路径(paths) \(\pi\) 的概率之和： \[\large p(\mathtt{l}|\mathtt{x})=\sum_{\pi \in \mathcal{B}^{-1}(\mathtt{l})}p(\pi | \mathtt{x})\] 即所有可映射为真实标签序列的预测序列(paths)的概率之和。 故 CTC Loss 可以表示为 \[\mathtt{CTC}_{Loss} = -ln(p(\mathtt{l}|\mathtt{x}))\]

假设目标标签序列为 \(\mathtt{l}=hello\)，输入序列长度为 12，则存在 \(\mathtt{l}^{12}=6^{12}=2176782336\) 个可能的路径，输入序列越长，标签集越大，可能的路径就越多，呈现指数级增长，显然计算所有的路径是不切实际的。

不过幸运的是，可以使用动态规划算法有效得计算出所有可能的真值标签概率。

动态规划算法

由于路径的数量会随着时间步数的增加呈指数增长，直接计算所有路径概率是不切实际的。CTC Loss 的计算通常采用动态规划算法(Forward-Backward Algorithm)来高效地计算目标标签序列的概率。该算法通过递归地计算部分路径概率，避免了重复计算，从而大大降低了计算复杂度。 首先构造一个表，横坐标是时间序列，纵坐标为将真实标签序列两两以符号 \(-\) 分隔，并且首尾各加一个 \(-\) 。使用 \(U'\) 表示经 \(-\) 符号扩展后的序列。

初始表

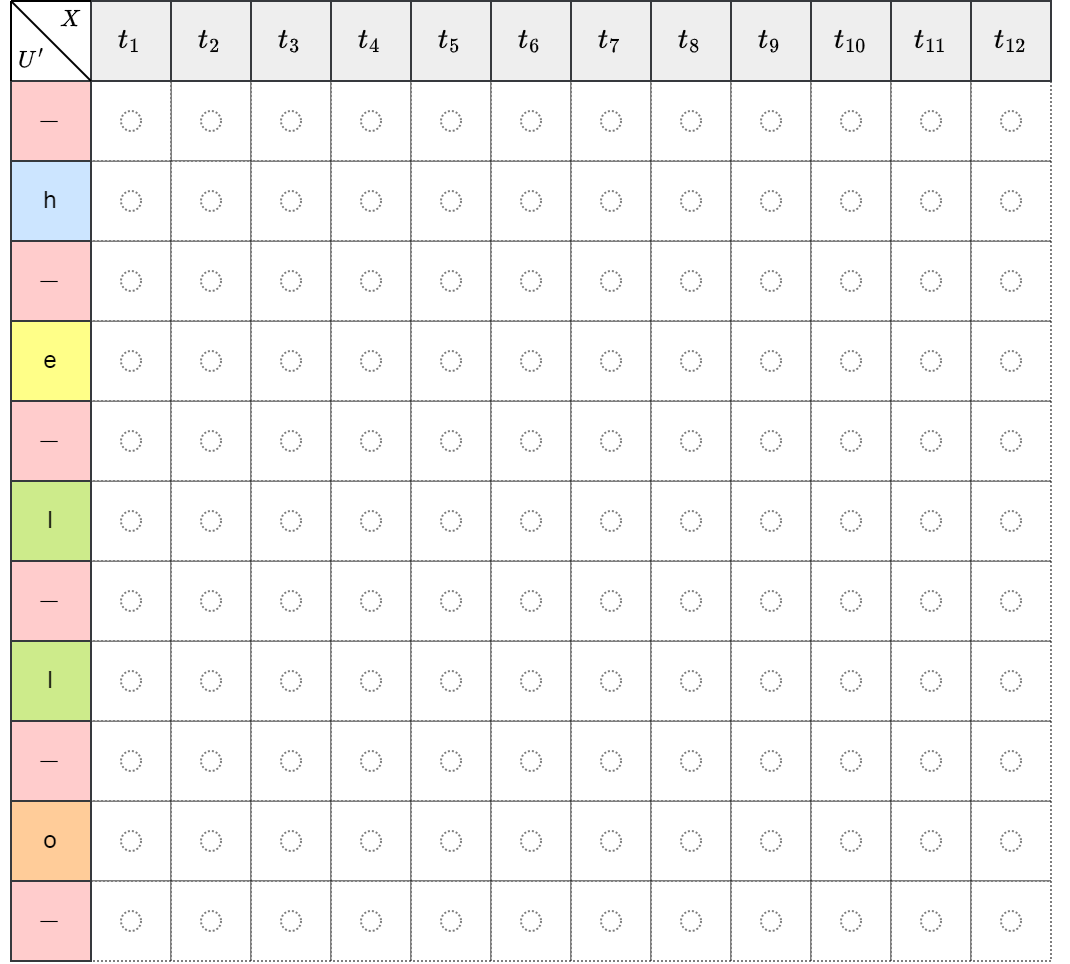
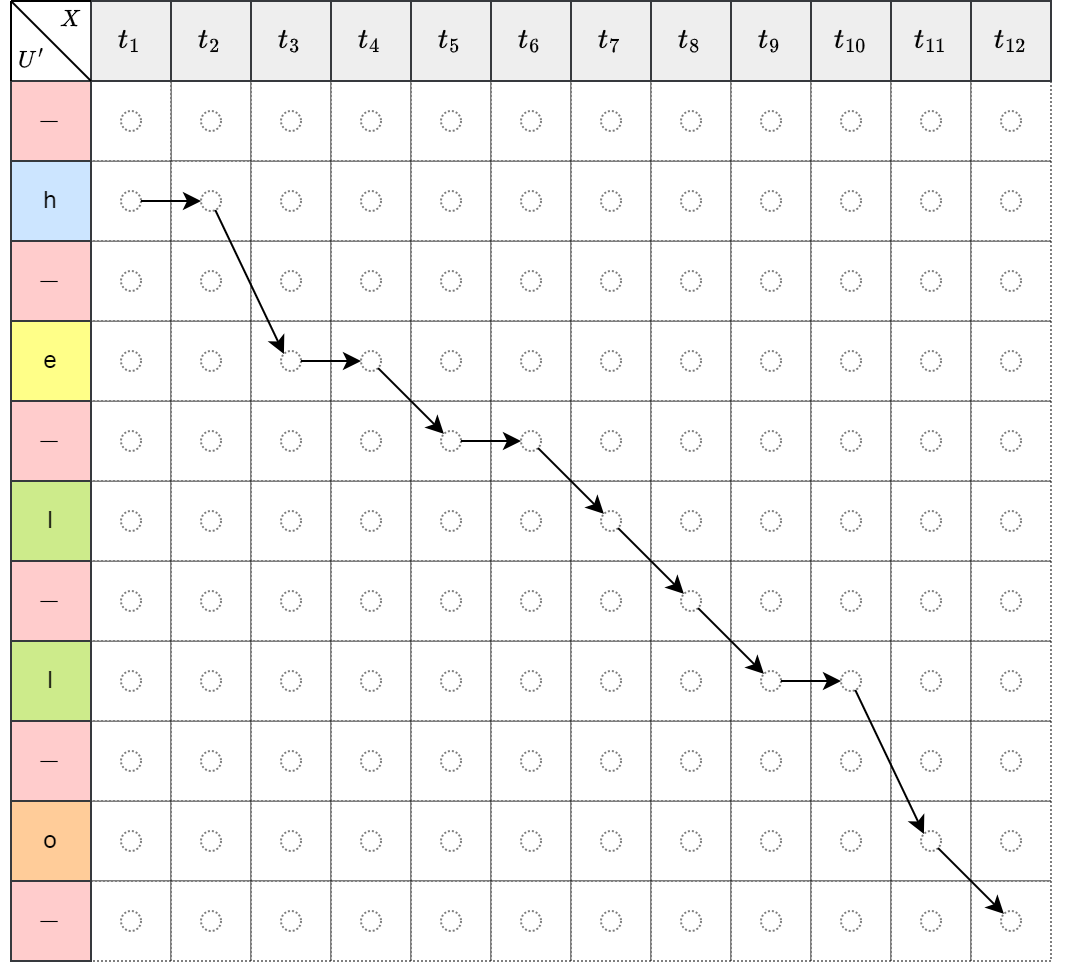
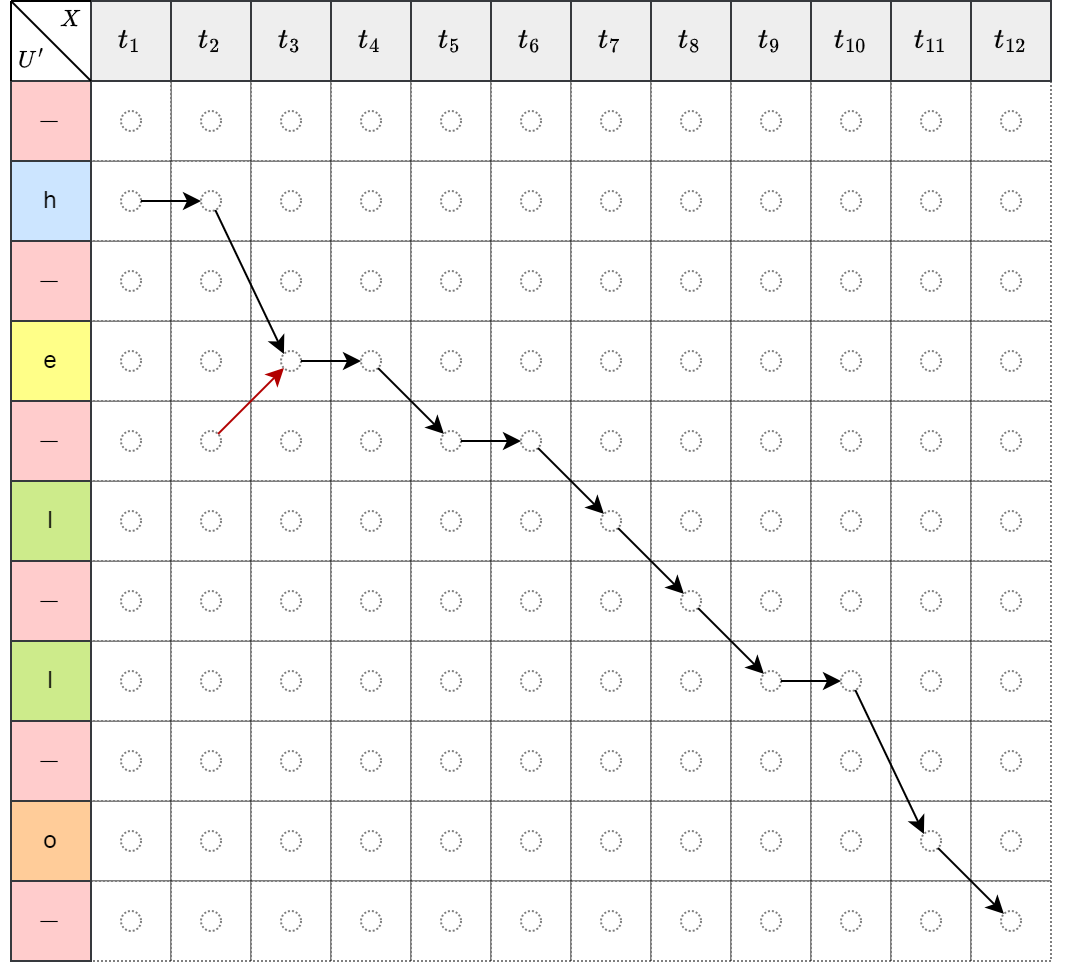
如下左图表示的映射关系为 \[\mathcal{B}(hheel-l-lo-)=hello\]，如下右图红色箭头是错误的，因为无法先预测第5个标签，再预测第4个标签，标签需要按顺序依次预测出，所以箭头只能向右或向下。

左图：一种路径示例
右图：错误箭头方向

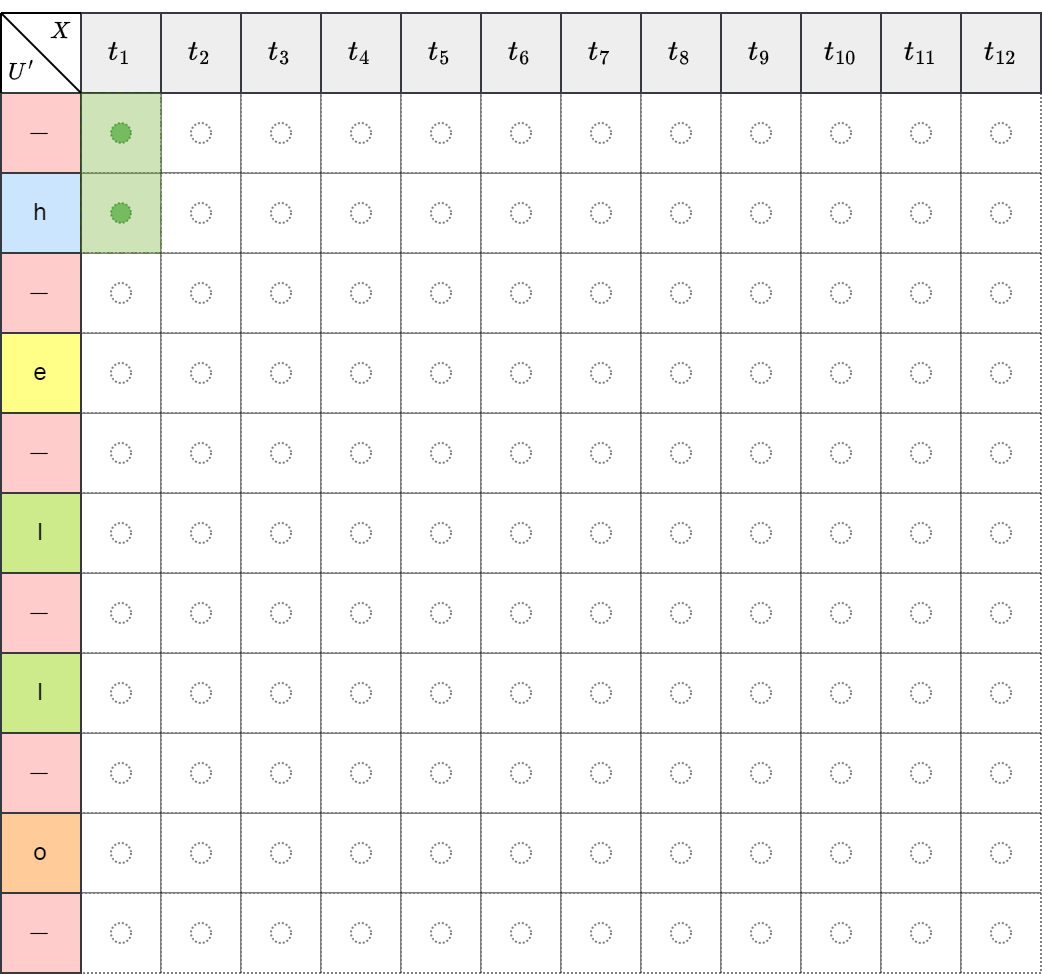
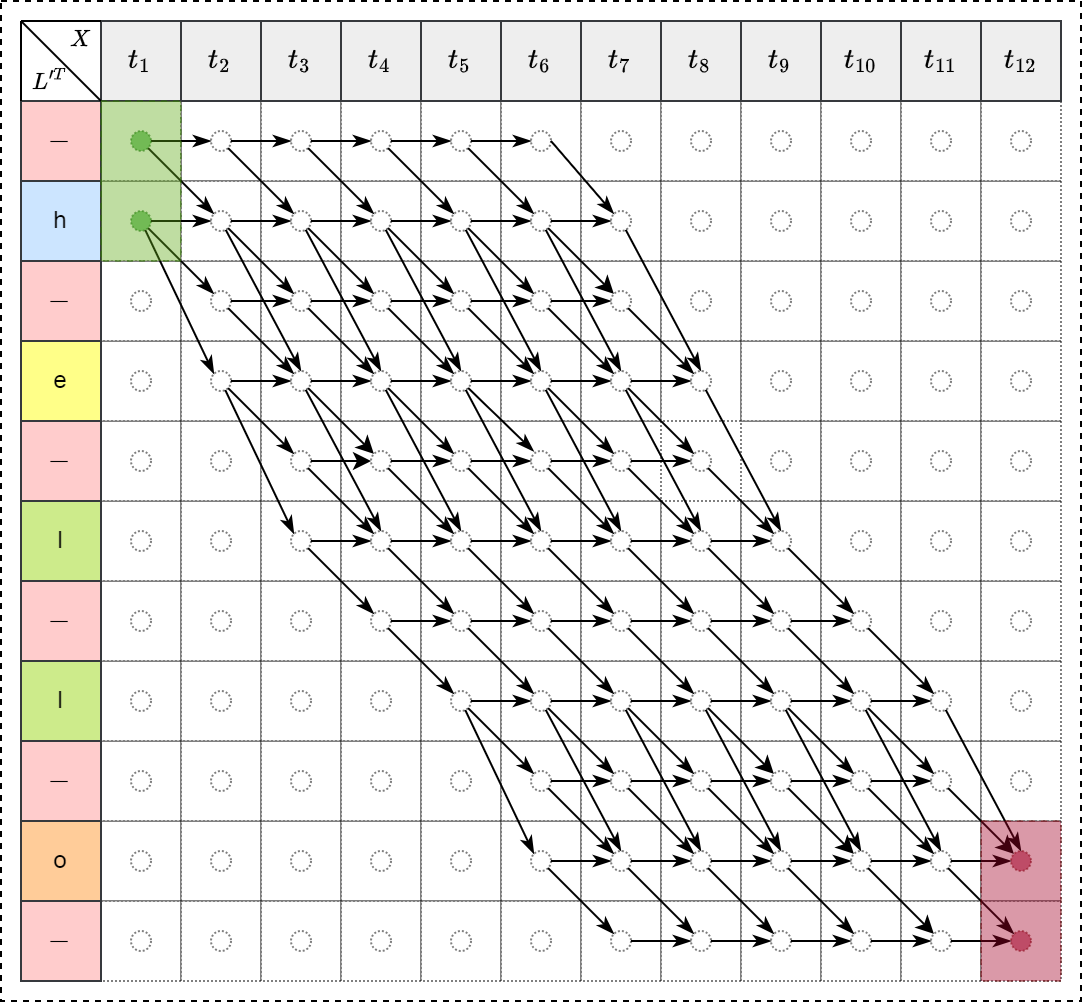
如下左图所示，初始 \(t_0\) 时刻只能处于 \(-\) 或 h 两个位置，经过搜索算法，依次经过 hello 所有的字母，所有可能的路径如下右图所示。

左图：初始状态
右图：动态规划后

前向过程

定义前向变量为 \[\Large \alpha_{t}(s) = \sum_{\pi \in N^T:\mathcal{B}(\pi_{1:t})=\mathtt{l}_{1:s}} \prod_{t'=1}^{t} \mathtt{y}_{\pi_{t'}}^{t'}\] 初始状态： \[\large \alpha_1(1)=y_b^1 \\ \alpha_1(2)=y_{\mathtt{l}_1}^1 \\ \alpha_1(s)=0, \forall s>2\] 递归公式为 \[\large \alpha_t(s) = \begin{cases} \Big(\alpha_{t-1}(s)+\alpha_{t-1}(s-1)\Big)y_{\mathtt{l}'_s}^t &\text{if } \mathtt{l'_s=b} \text{ or } \mathtt{l}'_{s-2}=\mathtt{l}'_s\\ \Big(\alpha_{t-1}(s)+\alpha_{t-1}(s-1)+\alpha_{t-1}(s-2)\Big)y_{\mathtt{l}'_s}^t &\text{otherwise } \end{cases}\]

前向过程示例

例如，当 \(t=3\) ， \(s=4\) 时，即 \(\alpha_{3}(4)\) 表示如下图：

\[\alpha_{3}(4)=p(\text{“-he”})+p(\text{“hhe”})+p(\text{“h-e”})+p(\text{“hee”})\]

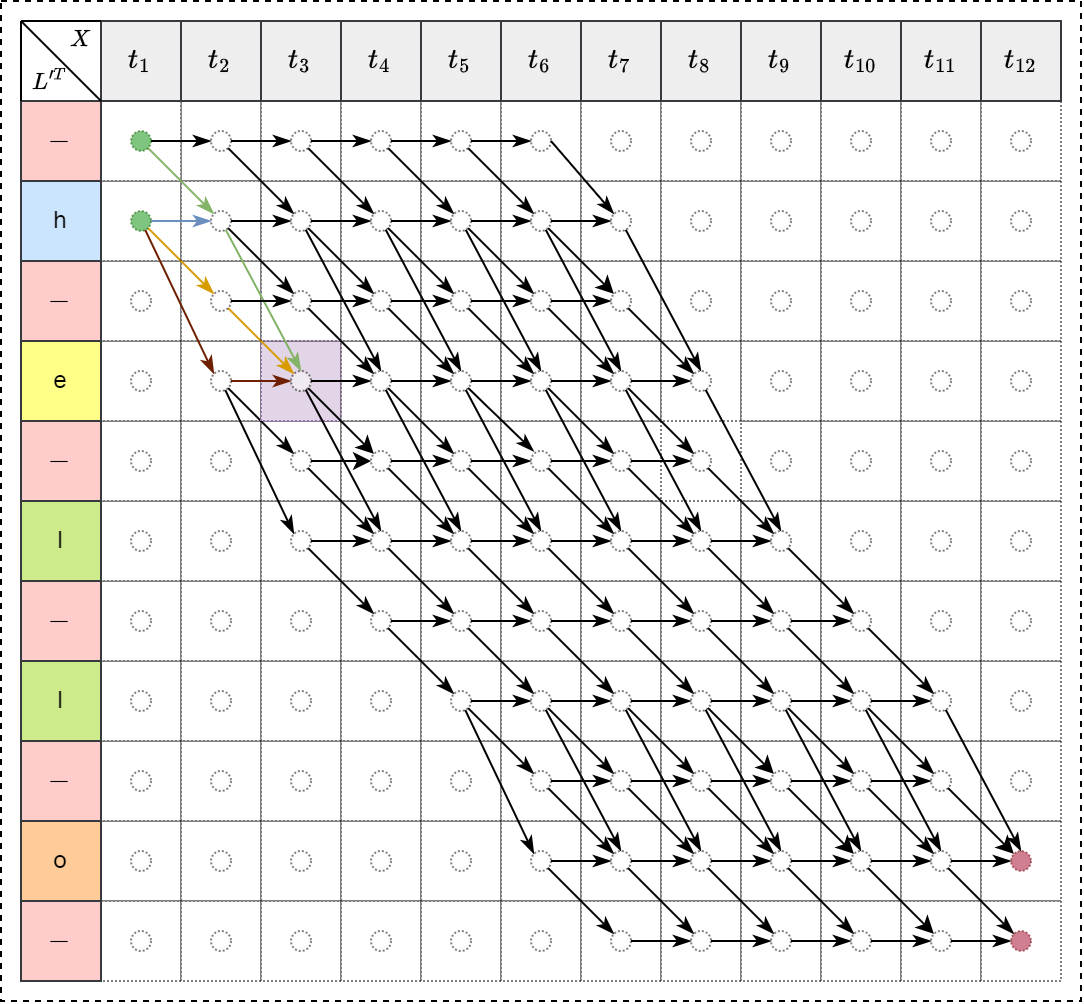
前向变量示例

存在三种递归情形

l=b
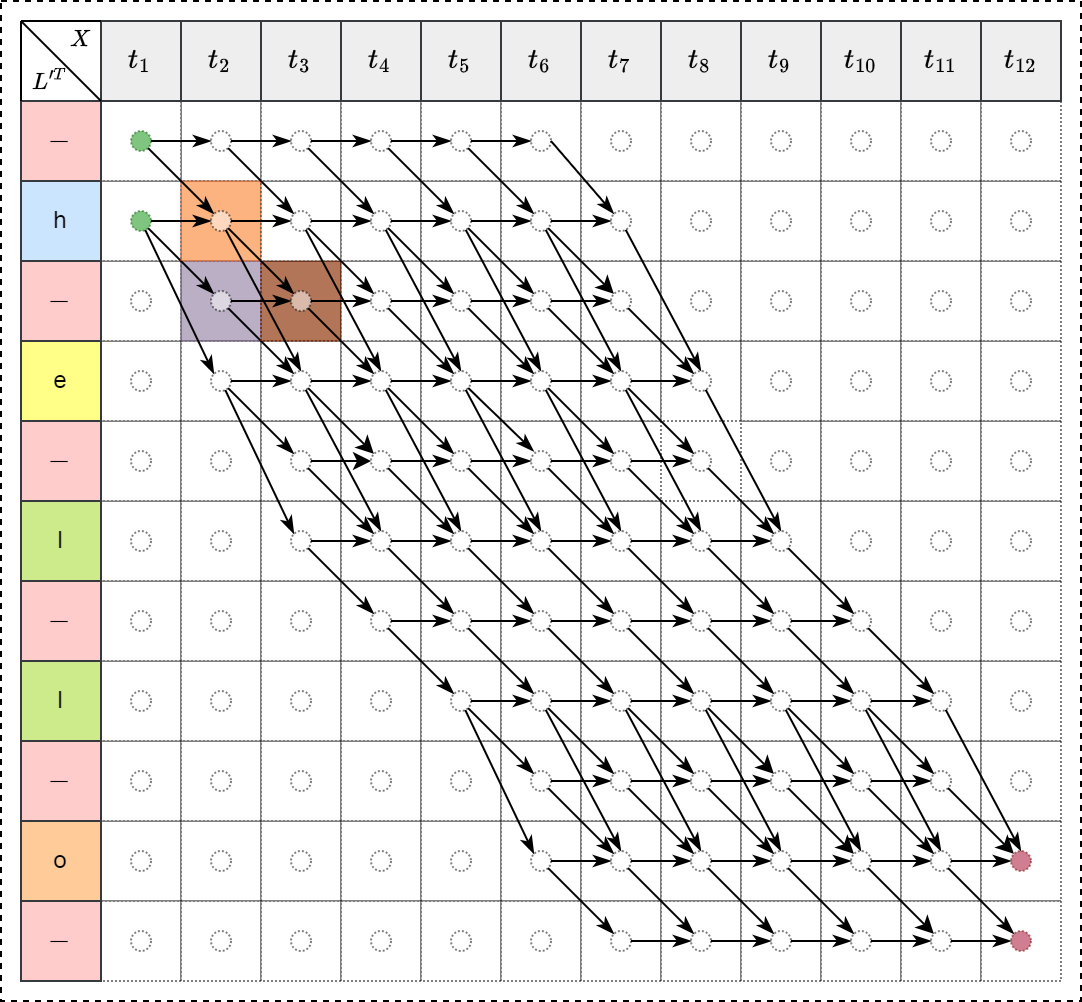
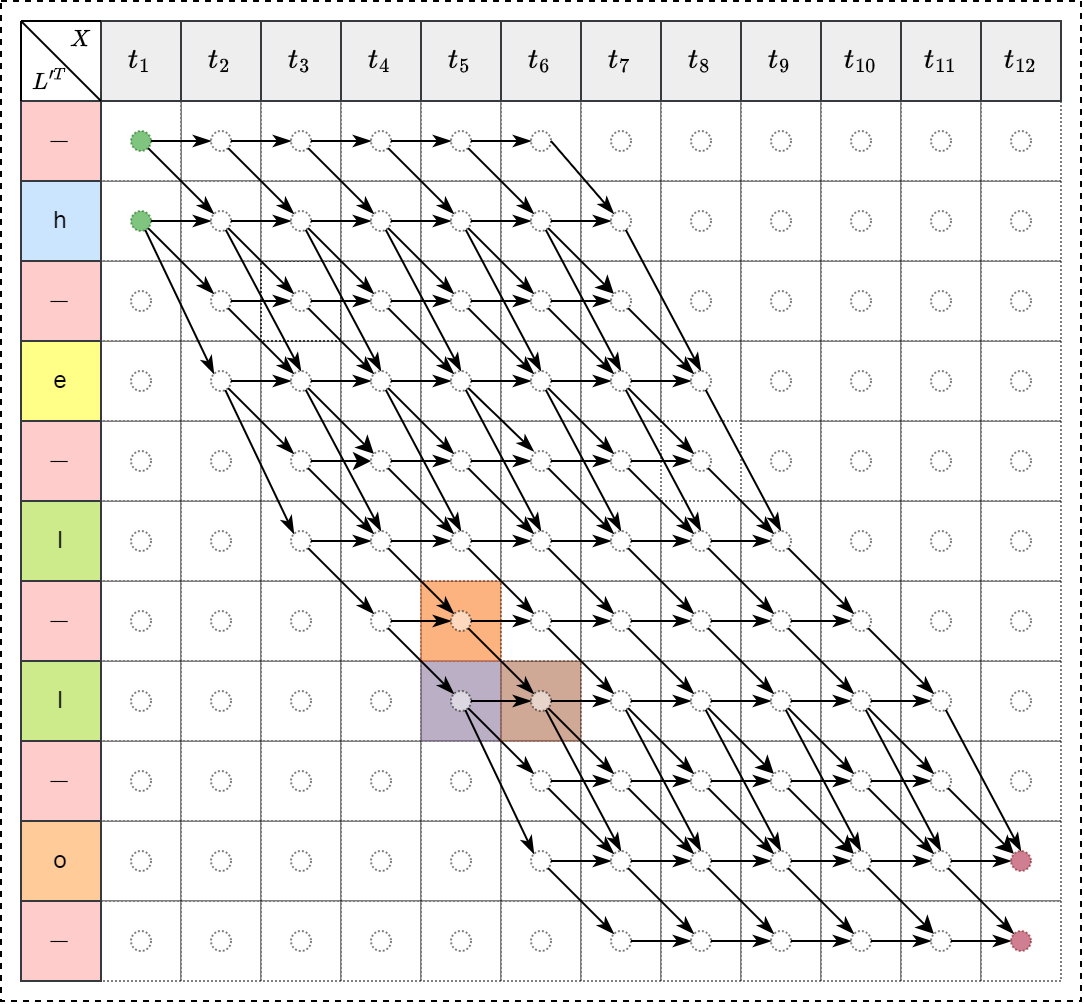
l(s-2)=l(s)
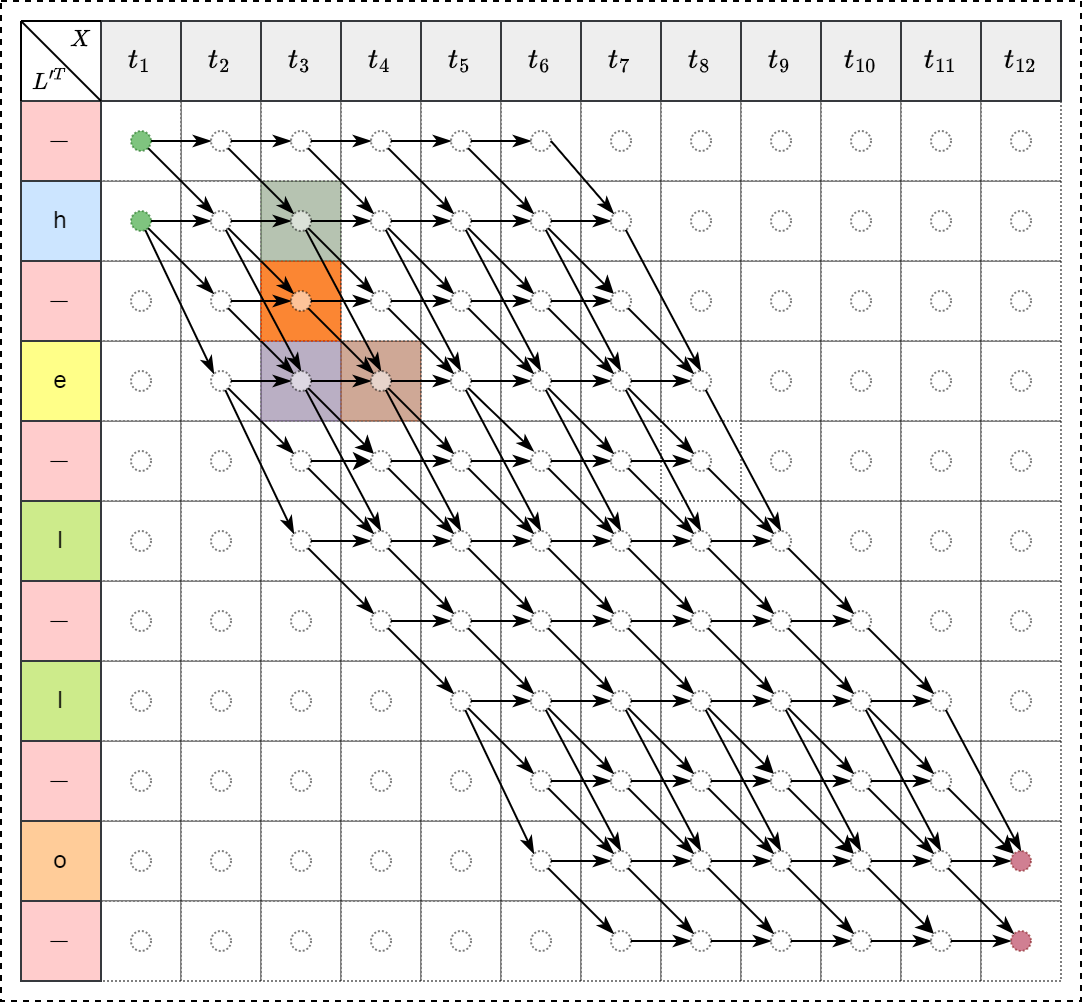
otherwise

计算CTC Loss

通过动态规划算法递归计算，最终可以计算出 \(\alpha_{12}(10)\) 和 \(\alpha_{12}(11)\) ，故真实标签的概率可以表示为： \[p(\text{“hello”}) = \alpha_{12}(11) + \alpha_{12}(10)\] 则对任意真值序列 \(\mathtt{l}\) 的概率可以表示为 \(T\) 时刻有或没有空白情况下 \(\mathtt{l}'\) 的总概率和： \[p(\mathtt{l}|\mathtt{x})=\alpha_{T}(|\mathtt{l}'|) + \alpha_{T}(|\mathtt{}l|'-1)\] 则 CTC loss 可以表示为 \[\text{CTC Loss} = -\ln(p(\text{“hello”})) = -\ln(\alpha_{12}(10) + \alpha_{12}(11))\]

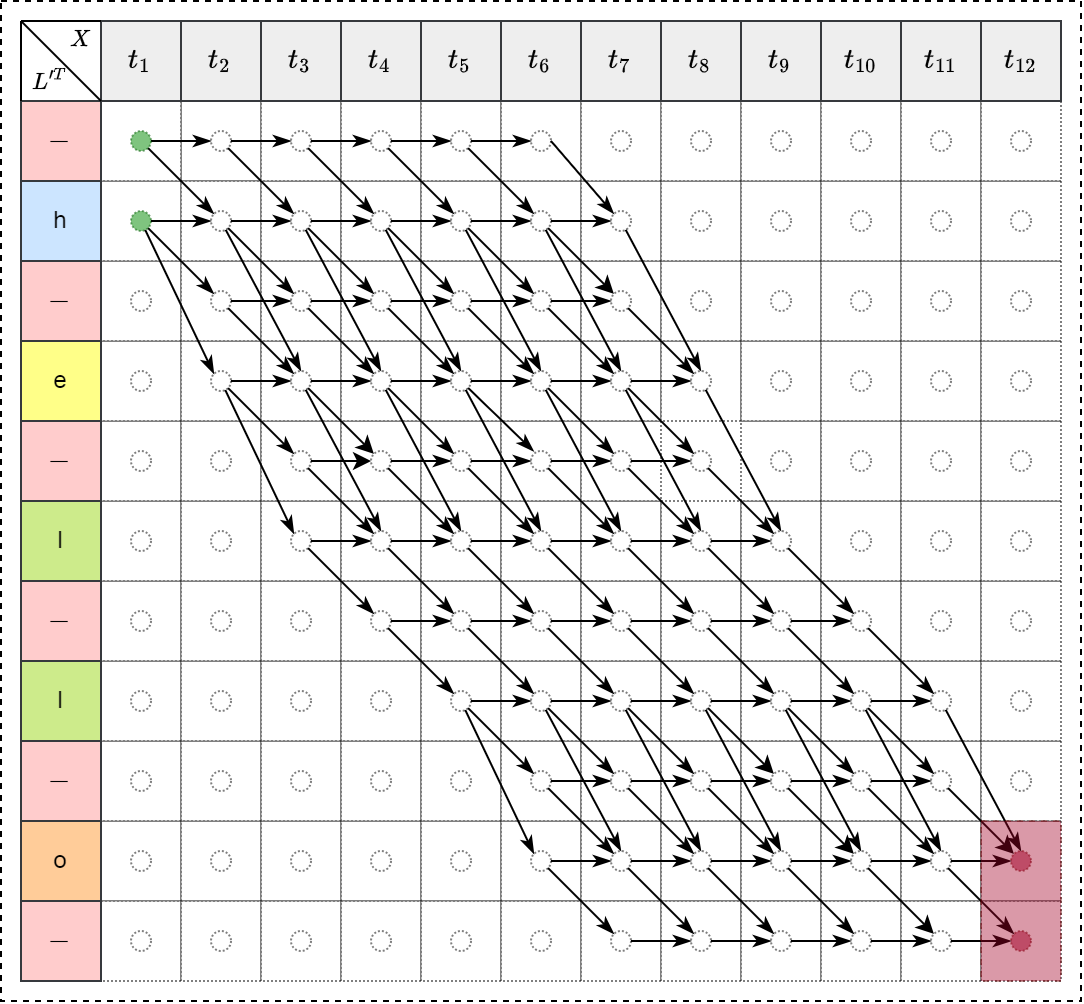
CTC Loss

后向过程

同样，后向变量定义为 \[\Large \beta_{t}(s) = \sum_{\pi \in N^T:\mathcal{B}(\pi_{t:T})=\mathtt{l}_{s:|\mathtt{l}|}} \prod_{t'=t}^{T} \mathtt{y}_{\pi_{t'}}^{t'}\]

初始状态为

\[\large \beta_T(|\mathtt{l}'|)=y_b^T \\ \beta_T(|\mathtt{l}'|-1)=y_{\mathtt{l}_{|\mathtt{l}|}}^T \\ \beta_T(s)=0, \forall s<|\mathtt{l}'|-1\]

递归公式为

\[\large \beta_t(s) = \begin{cases} \Big(\beta_{t+1}(s)+\beta_{t+1}(s+1)\Big)y_{\mathtt{l}'_s}^t &\text{if } \mathtt{l'_s=b} \text{ or } \mathtt{l}'_{s+2}=\mathtt{l}'_s\\ \Big(\beta_{t+1}(s)+\beta_{t+1}(s+1)+\beta_{t+1}(s+2)\Big)y_{\mathtt{l}'_s}^t &\text{otherwise } \end{cases}\]

后向过程示例

例如，当 $ t=10$ ， \(s=8\) 时，即 \(\beta_{10}(8)\) 表示如下图：

\[\beta_{10}(8)=p(\text{“lo”})+p(\text{“l-o”})+p(\text{“loo”})+p(\text{“lo-”})\]

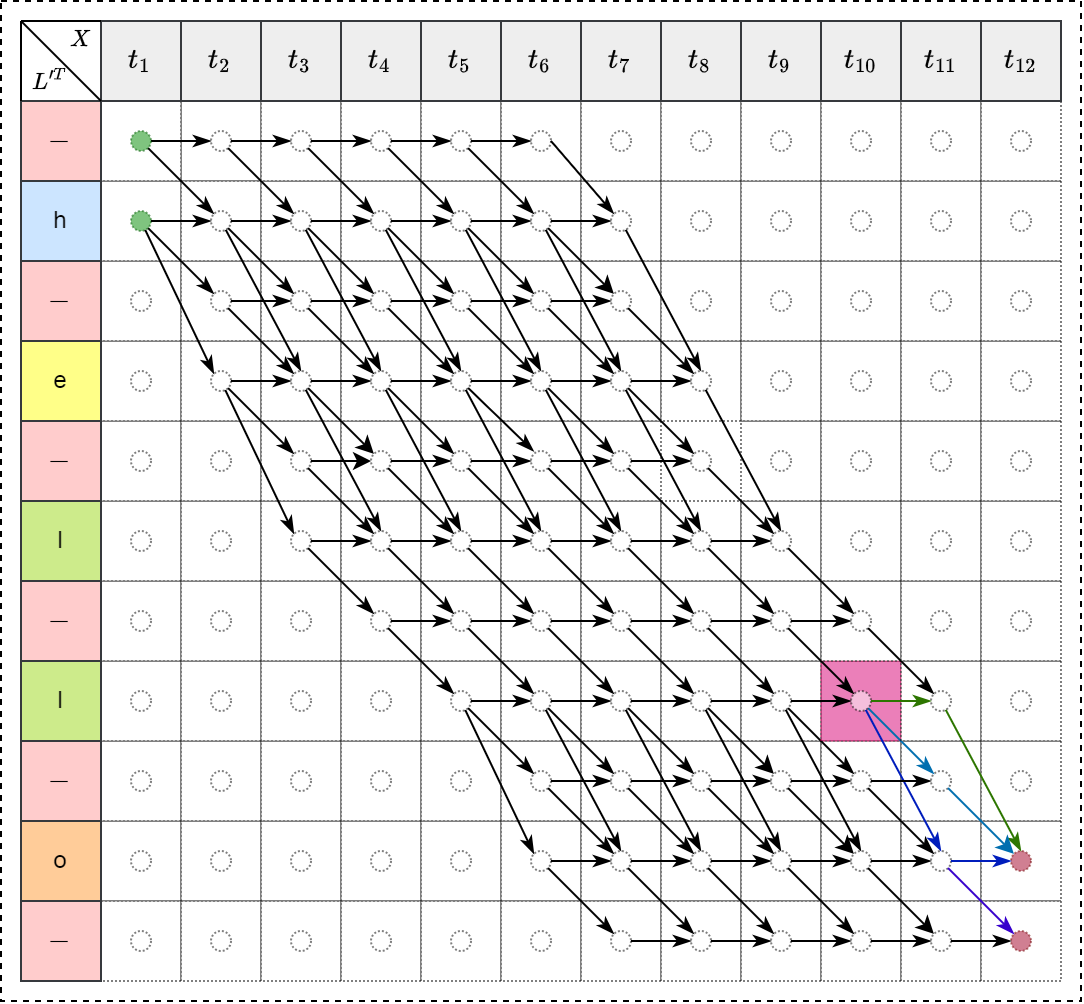
后向过程示例

前向后向对比

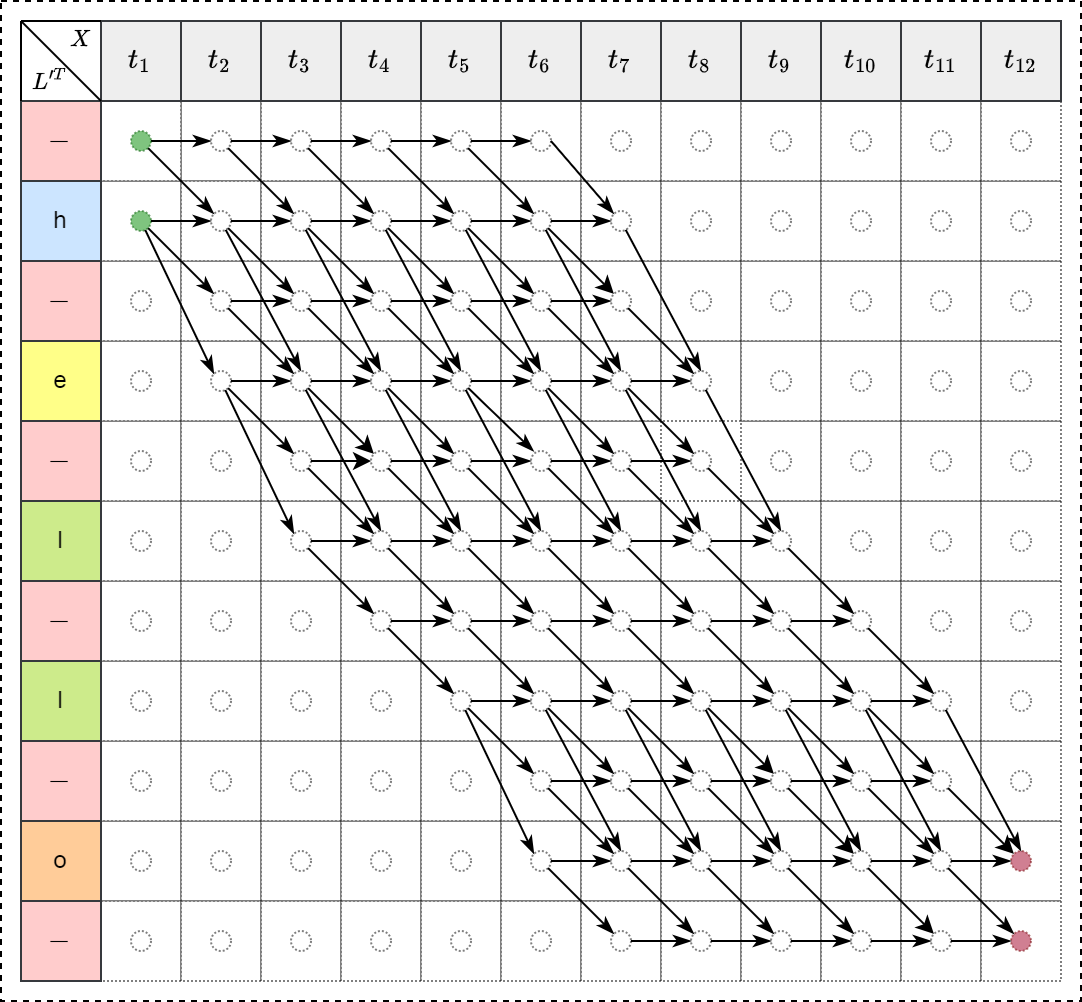
forward
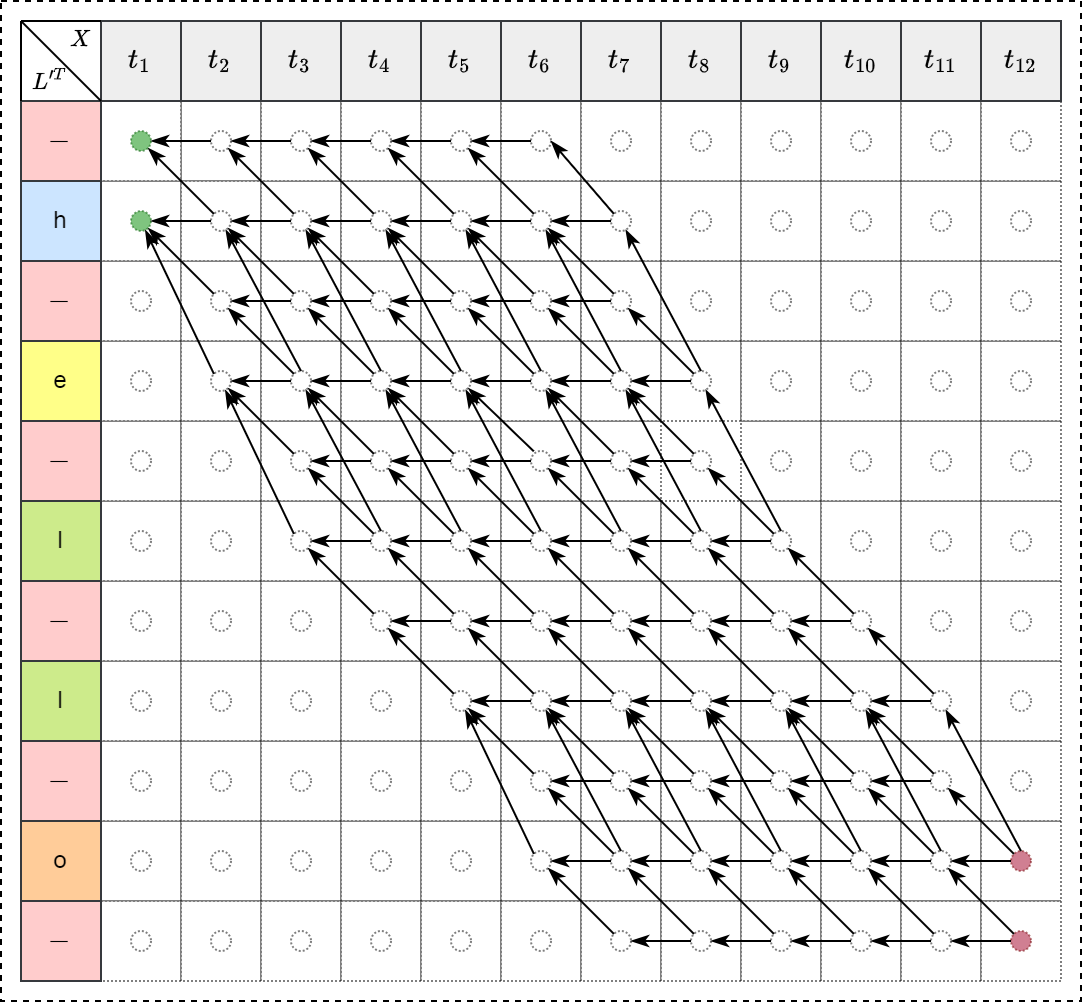
backward

计算梯度

考虑计算前向和后向变量相乘结果如下：

\[\begin{split} \alpha_{6}(6)*\beta_{6}(6)&=\Big(\alpha_{5}(4)+\alpha_{5}(5)+\alpha_{5}(6)\Big)y_{l}^6 * \Big(\beta_{7}(6)+\beta_{7}(7)\Big)y_{l}^6 \\ &=\Big(\alpha_{5}(4)y_{l}^6\beta_{7}(6)+\alpha_{5}(4)y_{l}^6\beta_{7}(7)+\alpha_{5}(5)y_{l}^6\beta_{7}(6)+\alpha_{5}(5)y_{l}^6\beta_{7}(7)+\alpha_{5}(6)y_{l}^6\beta_{7}(6)+\alpha_{5}(6)y_{l}^6\beta_{7}(7)\Big)y_{l}^6 \end{split}\] 故 \[\begin{split} \frac{\alpha_{6}(6)*\beta_{6}(6)}{y_{l}^6}=\alpha_{5}(4)y_{l}^6\beta_{7}(6)+\alpha_{5}(4)y_{l}^6\beta_{7}(7)+\alpha_{5}(5)y_{l}^6\beta_{7}(6)+\alpha_{5}(5)y_{l}^6\beta_{7}(7)+\alpha_{5}(6)y_{l}^6\beta_{7}(6)+\alpha_{5}(6)y_{l}^6\beta_{7}(7) \end{split}\] 上式可以表示为 \(t_{6}\) 时刻经过符号 \(l\) 的所有正确预测序列的概率和。 \[\large \begin{split} \frac{\alpha_{6}(6)*\beta_{6}(6)}{y_{l}^6}&=\sum_{\pi \in \mathcal{B}^{-1}(l):\pi_{6}=\text{“l”}}\prod_{t=1}^Ty_{\pi_{t}}^t \\ &=\sum_{\pi \in \mathcal{B}^{-1}(l):\pi_{6}=\text{“l”}}p(\pi|\mathtt{x}) \end{split}\]

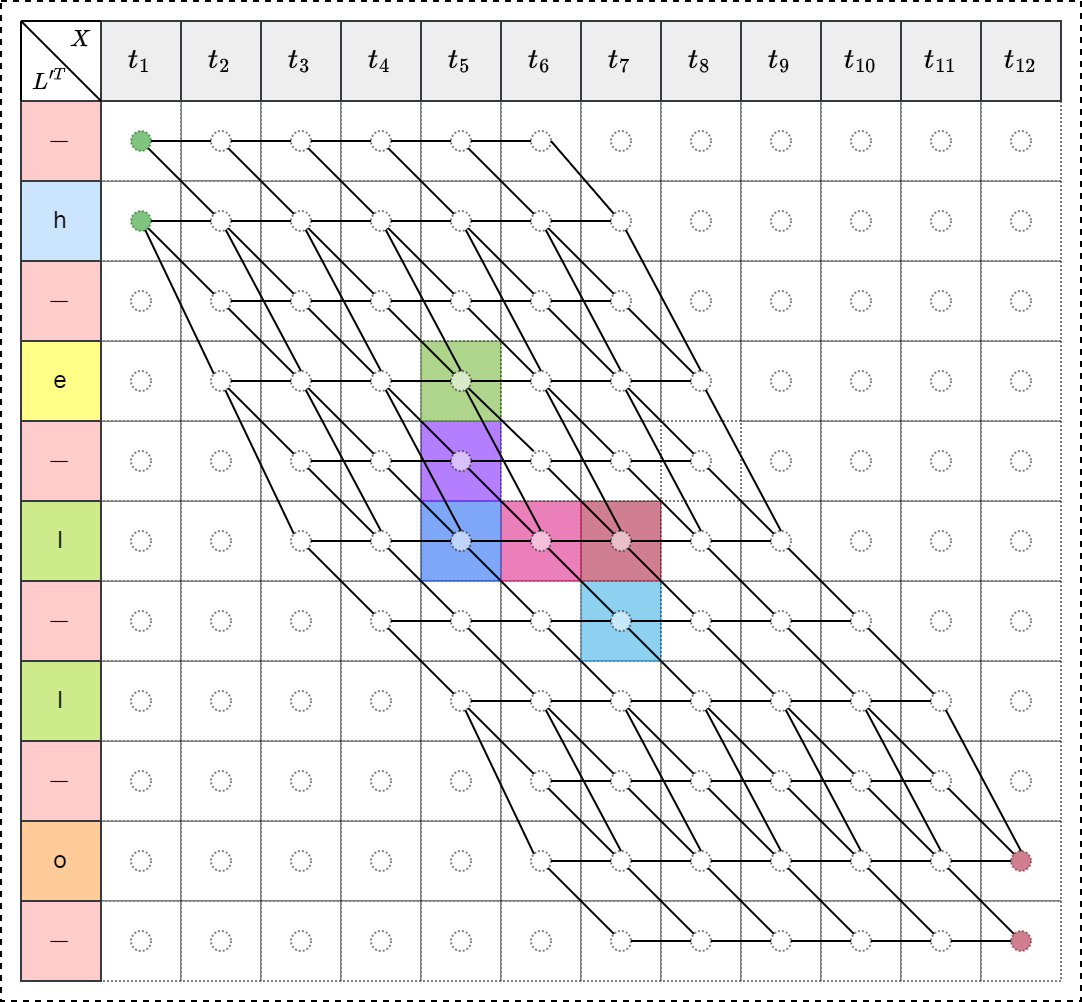
前向和后向变量

上述只计算了经过 \(l\) 字符的概率，则经过所有路径的总概率可以表示为 \[\large p(\mathtt{l}|\mathtt{x})=\sum_{s=1}^{10}\frac{\alpha_{6}(s)*\beta_{6}(s)}{y_{\mathtt{l}'_s}^6}\] 那么任意时刻的所有可能路径的概率之和表示为 \[\large p(\mathtt{l}|\mathtt{x})=\sum_{s=1}^{|\mathtt{l}'|}\frac{\alpha_{t}(s)*\beta_{t}(s)}{y_{\mathtt{l}'_s}^t}\]

反向传播

学习的目标是最大化 \(p(\mathtt{l}|\mathtt{x})\)，等效为最小化 \(-\ln(p(\mathtt{l}|\mathtt{x}))\) ，这就是我们的目标函数，在反向传播时，我们需要对神经网络的每一个预测输出 \(y_k^t\) 求偏导，故 \[\frac{\partial \big(-\ln(p(\mathtt{l}|\mathtt{x}))\big)}{\partial y_k^t}=-\frac{1}{p(\mathtt{l}|\mathtt{x})}*\frac{\partial p(\mathtt{l}|\mathtt{x})}{\partial y_k^t}\] 最终转换为如何求解 \(\frac{\partial p(\mathtt{l}|\mathtt{x})}{\partial y_k^t}\)。 由于 \[\large p(\mathtt{l}|\mathtt{x})=\frac{\alpha_{t}(1)*\beta_{t}(1)}{y_{\mathtt{l}'_1}^t} + \frac{\alpha_{t}(2)*\beta_{t}(2)}{y_{\mathtt{l}'_2}^t} + ... +\frac{\alpha_{t}(s)*\beta_{t}(s)}{y_{\mathtt{l}'_s}^t} + ... +\frac{\alpha_{t}(|\mathtt{l}'|)*\beta_{t}(|\mathtt{l}'|)}{y_{|\mathtt{l}'|}^t}\] 若 \(t\) 时刻经过 \(k\) ，则不会经过其它字符，也就是说其它项可以被视为常数项。当 \(\mathtt{l}'_s=k\) 时， \[\frac{\partial p(\mathtt{l}|\mathtt{x})}{\partial y_6^t} = -\frac{1}{(y_{6}^t)^2}\big(\alpha_{t}(6)*\beta_{t}(6)\big)\] 定义标签为 \(k\) 的集合 \(\mathtt{lab}(\mathtt{l},k)=\{s:\mathtt{l}'_s=k\}\) ，则 \[\large \frac{\partial p(\mathtt{l}|\mathtt{x})}{\partial y_k^t} = -\frac{1}{(y_{k}^t)^2}\sum_{s \in lab(\mathtt{l},k)}\alpha_{t}(s)*\beta_{t}(s)\]

三种情形

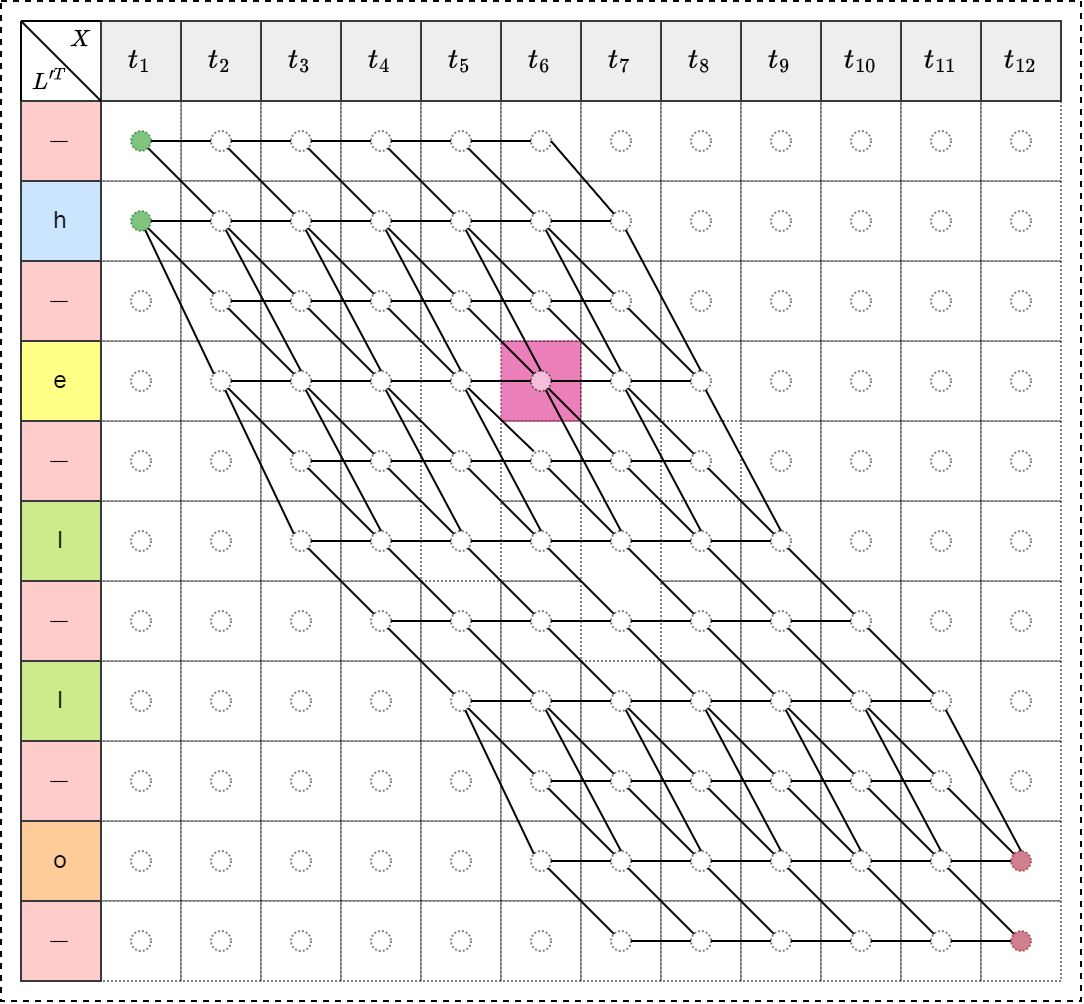
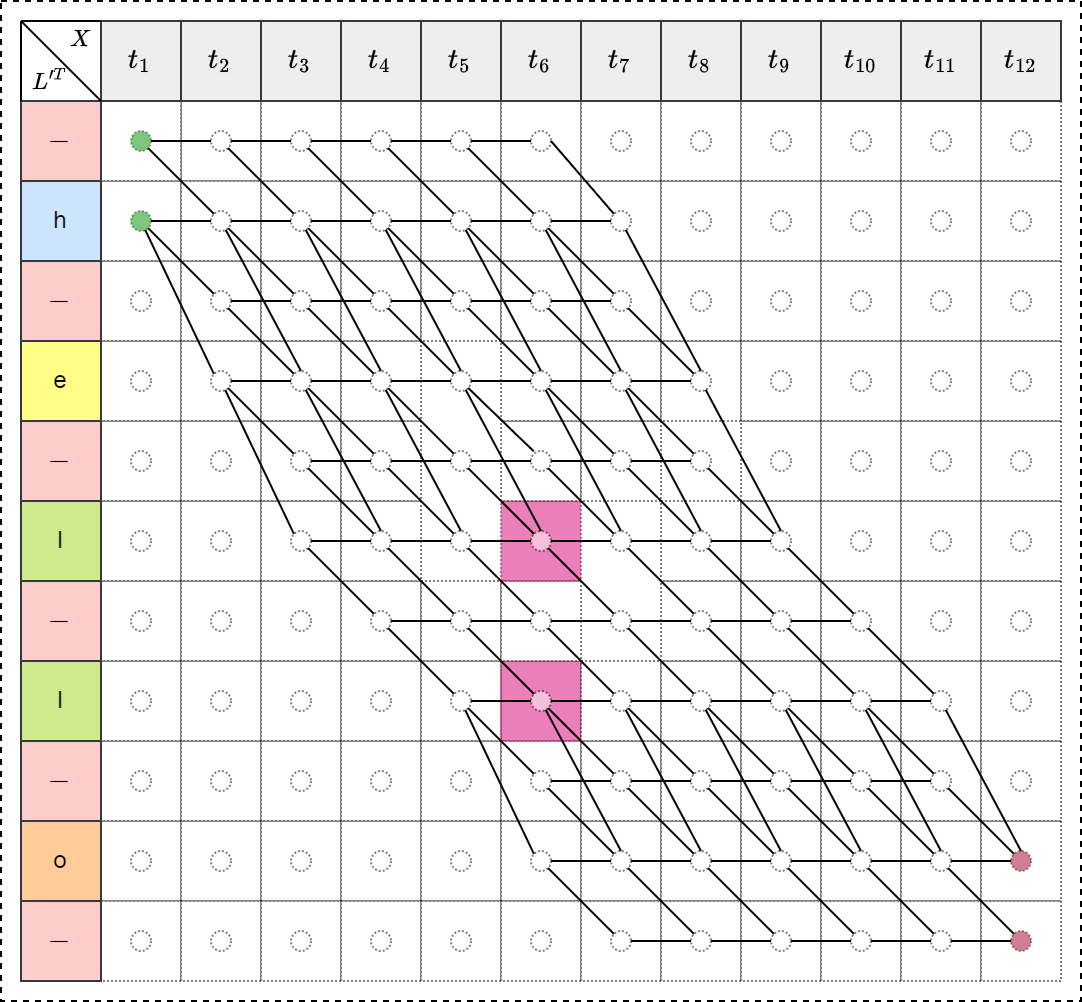
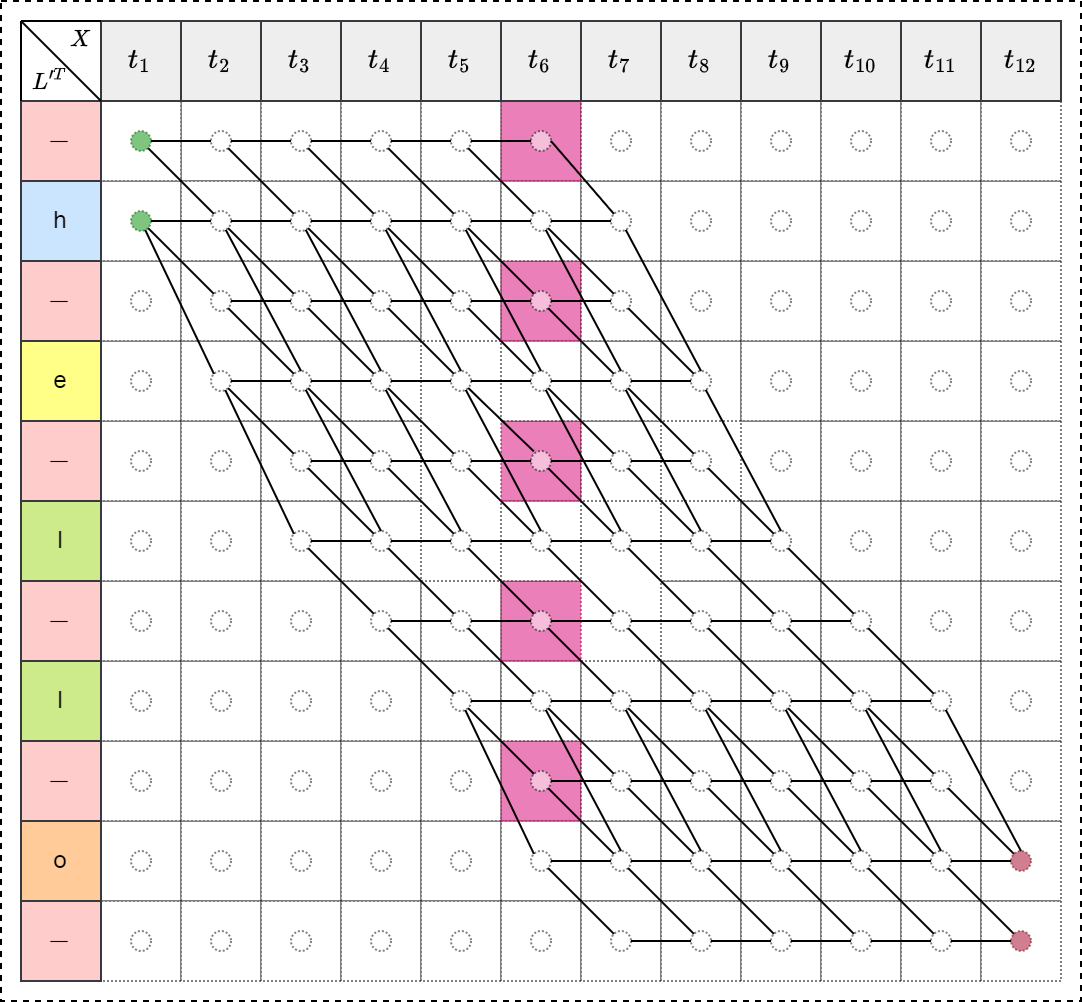
image.png
image.png
image.png

总结

  1. 前向变量 \(\alpha_t(s)\) 用于计算损失；
  2. 后向变量 \(\beta_t(s)\) 用于方便计算梯度；