语音活动检测(VAD)
概述
在语音活动检测(VAD)中,有多种模型可供选择,每种模型都有其独特的特点和应用场景。
Webrtc-VAD 是一种广泛应用的语音活动检测模型,它基于语音信号的能量和过零率等特征进行检测。SileroVAD 则采用了深度学习技术,通过对大量语音数据的学习,能够更准确地检测语音活动。FSMN-VAD 结合了前馈序列记忆网络,在处理长语音序列时表现出色。
这些模型在不同的环境和应用中都发挥着重要作用。例如,在电话会议中,Webrtc-VAD 可以有效地过滤背景噪声,提高语音质量;在智能语音助手等场景中,SileroVAD 和 FSMN-VAD 能够更准确地识别用户的语音指令。
未来,随着技术的不断发展,语音活动检测模型将不断改进和创新,为语音通信和交互提供更好的支持。
Webrtc-VAD
该模型使用非机器学习方法,是Google为WebRTC项目开发的快速、且免费的VAD模块。它基于语音信号的能量和过零率等特征进行检测。Webrtc-VAD 主要包括以下几个步骤:
- 音频预处理:对输入的音频信号进行预处理,包括滤波、降噪等操作,以提高后续检测的准确性。
- 特征提取:提取音频信号的能量、过零率等特征。
- 阈值判断:根据预设的阈值,判断音频信号是否包含语音活动。
- 后处理:对检测结果进行后处理,如平滑处理等,以提高检测结果的稳定性。
Webrtc-VAD 具有计算量小、速度快的优点,适用于实时性要求较高的语音通信场景。
Silero-VAD
SileroVAD 是一种基于深度学习技术的轻量级语音活动检测模型。文件大小仅有 2.2MB ,支持任意采样率的 PCM 格式输入数据,其主要由卷积和 LSTM 等结构组成。通过对大量语音数据的学习,能够更准确地检测语音活动。SileroVAD 主要包括以下几个步骤:
- 音频预处理:对输入的音频信号进行预处理,包括滤波、降噪等操作,以提高后续检测的准确性。
- 特征提取:使用深度学习模型自动提取音频信号的特征。
- 模型训练:使用大量的语音数据对深度学习模型进行训练,以提高模型的准确性。
- 阈值判断:根据预设的阈值,判断音频信号是否包含语音活动。
- 后处理:对检测结果进行后处理,如平滑处理等,以提高检测结果的稳定性。
SileroVAD 具有检测准确率高、适应性强的优点,适用于各种复杂的语音环境。
如下图所示,是该模型的输入和输出结构图:
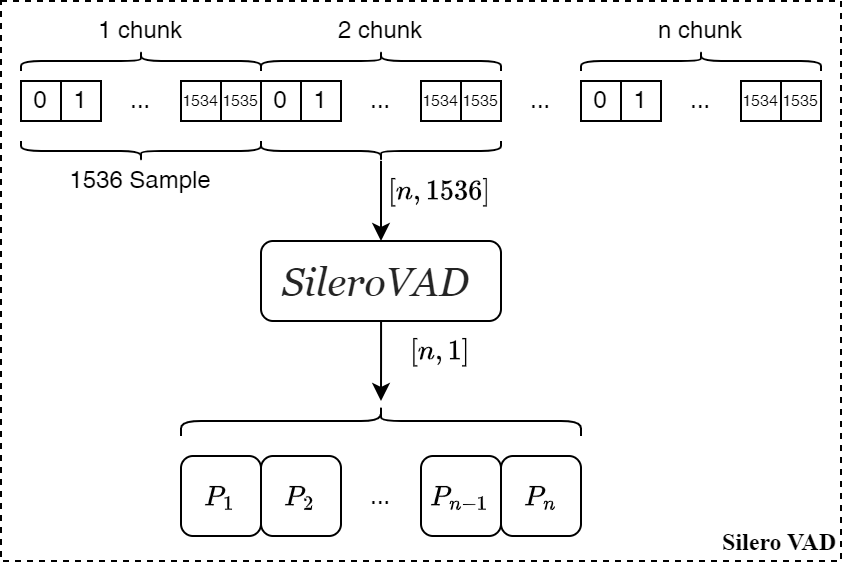
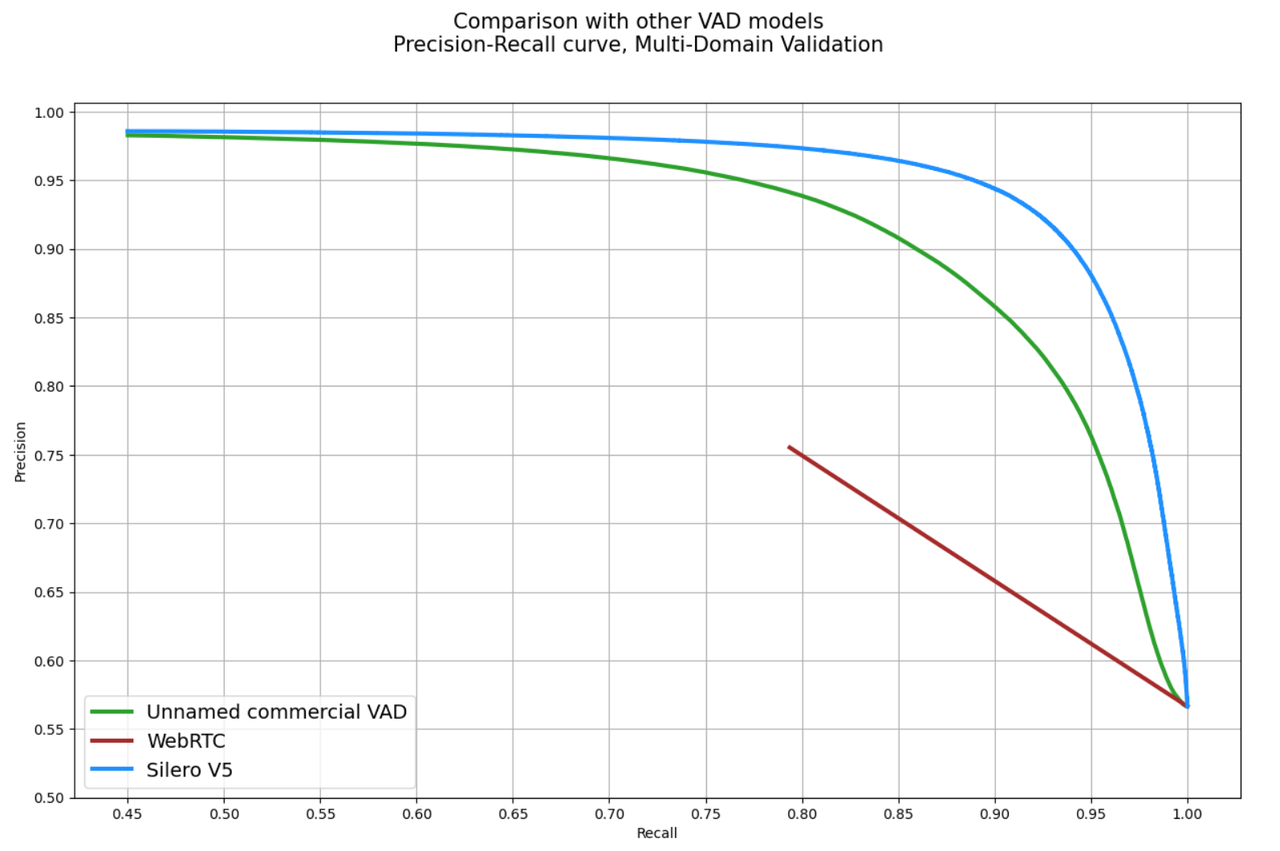
精度数据如下图:
参考链接
voice activity detector for the browser
Silero VAD - pre-trained enterprise-grade Voice Activity Detector
FSMN-VAD
FSMN-VAD 结合了前馈序列记忆网络,在处理长语音序列时表现出色。它的主要特点包括:
- 能够处理长语音序列:FSMN-VAD 可以有效地处理长语音序列,避免了传统模型在处理长序列时的性能下降问题。
- 适应性强:FSMN-VAD 可以适应不同的语音环境和应用场景,具有较强的泛化能力。
- 检测准确率高:FSMN-VAD 能够更准确地检测语音活动,提高了语音通信和交互的质量。
模型结构
模型的关键结构是引入了FSMN模块,用于解决长序列相关性问题。
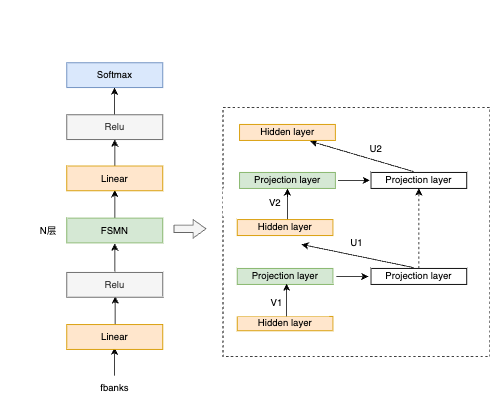
体验网址
FSMN-Monophone VAD 模型介绍
关于FSMN结构的发展
张仕良,博士,毕业于中国科学技术大学语音及语言信息处理国家工程实验室。 研究领域主要包括语音识别,机器> 学习算法等,提出了FSMN、HOPE、FOFE等模型。博士毕业以后加入阿里巴巴智能语音交互团队,目前主要负责语音> 识别,特别是声学建模相关算法的研究。
FSMN(中科大-讯飞[2015])
前馈序列记忆网络(feedforward sequential memory networks-FSMN),是一种专门为序列建模设计的神经网络结构。它旨在解决传统 RNN 在处理长序列时遇到的梯度消失和计算效率低下的问题。
FSMN受到了数字信号处理中滤波器设计知识的启发,任何无限脉冲响应(IIR)滤波器都可以用高阶有限脉冲响应(FIR)滤波器很好地逼近,由于RNN中的循环层在概念上可以看作一阶IIR滤波器,因此它应该能够被高阶FIR滤波器精确逼近。因此,我们通过在隐藏层中加入一些采用类似于FIR滤波器的抽头延迟线结构的记忆块来扩展标准的前馈全连接神经网络。 FSMN中可学习的FIR类记忆块可以将长上下文信息编码成固定大小的表示,这有助于模型捕获长期依赖。
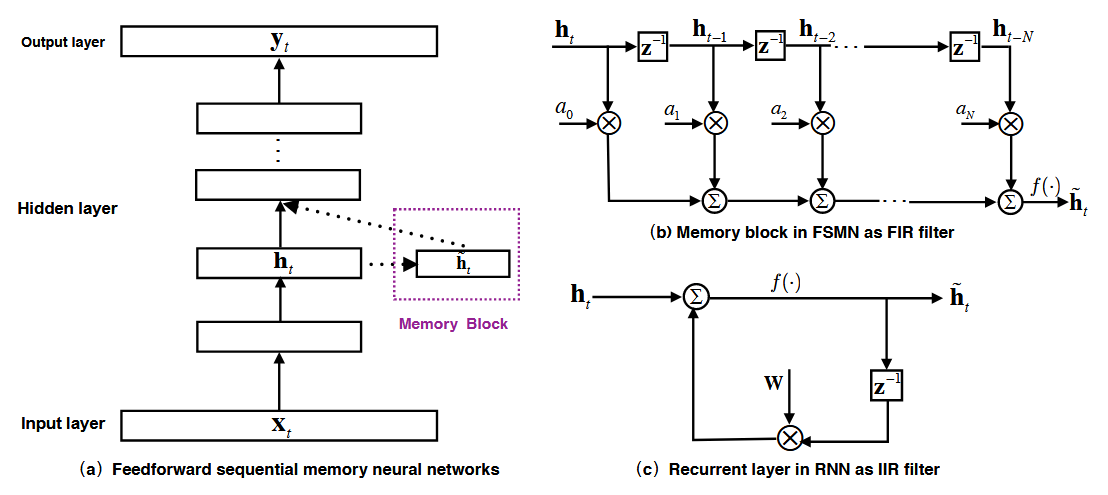
标量和矢量FSMN
- 标量FSMN(sFSMN):
\[\large \tilde{h}_{t}^{l}=\sum_{i=0}^{N}a_{i}^{l}\cdot h_{t-i}^l\]
其中, \(a^l = \{a_0^l,a_1^l,...,a_N^l\}\) 表示所有 N+1 个时不变系数。
- 矢量FSMN(vFSMN)
\[\large \tilde{h}_{t}^{l}=\sum_{i=0}^{N}\mathtt{a}_{i}^{l}\odot h_{t-i}^l\]
其中 \(\odot\) 表示两个大小相同的向量的逐元素相乘,所有系数向量均记作 \(A^l = \{\mathtt{a}_0^l,\mathtt{a}_1^l,...,\mathtt{a}_N^l,\}\)。
单向和双向FSMN
- 单向FSMN
上述只考虑过去信息的称为单向FSMN,这些单向FSMN适用于仅可获得过去信息的某些应用,例如语言建模。
- 双向FSMN
双向
\[\large \tilde{h}_{t}^{l}=\sum_{i=0}^{N_1}a_{i}^{l}\cdot h_{t-i}^l + \sum_{j=1}^{N_2}c_j^l \cdot h_{t+j}^l\]
\[\large \tilde{h}_{t}^{l}=\sum_{i=0}^{N_1}\mathtt{a}_{i}^{l}\cdot h_{t-i}^l + \sum_{j=1}^{N_2}\mathtt{c}_j^l \cdot h_{t+j}^l\]
则下一层隐藏层的输出表示为
\[h_t^{l+1}=f(W^lh_t^l+\tilde{W}^l\tilde{h}^l+b^l)\]
cFSMN(中科大-讯飞[2016])
鉴于内存块引入的额外参数,提出了一种改进的FSMN架构,即紧凑型FSMN (compact feedforward sequential memory networks-cFSMN),以简化FSMN架构并加快学习速度。
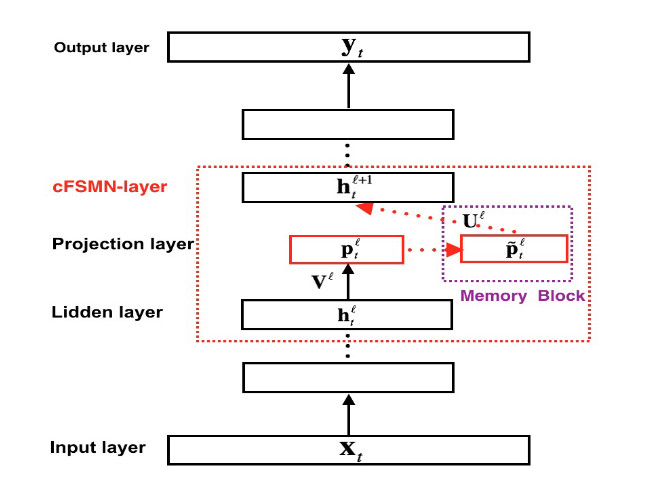
cFSMN层由三部分组成:
- 线性投影层;
- 记忆块;
- 从记忆块到下一隐藏层的权重连接。 与FSMN相比,cFSMN可以看作是在非线性隐层之后插入一个更小的线性投影层,并将记忆块添加到线性投影层而不是隐藏层。

- 单向cFSMN
\[\large \tilde{\mathtt{p}}_t^l=\mathtt{p}_t^l + \sum_{i=0}^{N}\mathtt{a}_i^l \odot \mathtt{p}_{t-i}^l\]
- 双向cFSMN
\[\large \tilde{\mathtt{p}}_t^l=\mathtt{p}_t^l + \sum_{i=0}^{N_1}\mathtt{a}_i^l \odot \mathtt{p}_{t-i}^l + \sum_{j=1}^{N_2}\mathtt{c}_i^l \odot \mathtt{p}_{t+j}^l\]
其中, \(\mathtt{p}_t^l=\mathtt{V}^lh_t^l+b^l\) 表示第 \(l\) 个线性投影层的线性输出。则下一层隐藏层的输出表示为
\[\large h_t^{l+1}=f(U^{l}\tilde{\mathtt{p}}_t^l +b^{l+1})\]
Deep-FSMN(阿里[2018])
如果我们想通过直接增加更多cFSMN层来训练更深的cFSMN,则会遭受梯度消失问题。受近期关于使用跳跃连接训练非常深的神经网络架构(例如残差网络或高速网络)工作的启发,提出了一种改进的FSMN架构,即深度FSMN(DFSMN)。
如上图所示,在标准cFSMN的存储块之间添加了一些跳跃连接(skip connections),其中下层存储块的输出可以定向流向高层存储块。在反向传播过程中,高层的梯度也可以直接赋予低层,这有助于克服梯度消失问题。
\[\large \tilde{\mathtt{p}}_t^l=\mathcal{H}(\tilde{\mathtt{p}}_t^{l-1}) + p_t^l+ \sum_{i=0}^{N_1^l}\mathtt{a}_i^l \odot \mathtt{p}_{t-s_1*i}^l + \sum_{j=1}^{N_2^l}\mathtt{c}_i^l \odot \mathtt{p}_{t+s_2*j}^l\]
其中,
- \(\mathtt{p}_t^l=V^lh_t^l+b^l\) 表示第 \(l\) 个线性投影层的线性输出;
- \(\tilde{\mathtt{p}}_t^l\) 表示第 \(l\) 个内存块的输出;
- \(N_1^l\) 和 \(N_2^l\) 分别表示第 \(l\) 个内存块的回溯阶数和前瞻阶数;
- \(\mathcal{H}(\cdot)\) 表示内存块内的跳跃连接,可以是任何线性或非线性变换。例如,如果内存块的维度相同,我们可以使用如下所示的恒等映射: \(\tilde{\mathtt{p}}_t^{l-1}=\mathcal{H}(\tilde{\mathtt{p}}_t^{l-1})\)。
- \(s_1\) 和 \(s_2\) 分别表示回溯和前瞻滤波器的步长;
对于语音信号,由于帧与帧之间存在重叠,相邻帧的信息具有很强的冗余性。类似于WaveNet [26]中的扩张卷积层,我们在内存块中加入步长因子以去除这种冗余性。