PointNet 模型分析 (3D 对象检测)

发表于 更新于 分类于 ， 阅读次数： 7 Changyan： 0 Disqus：

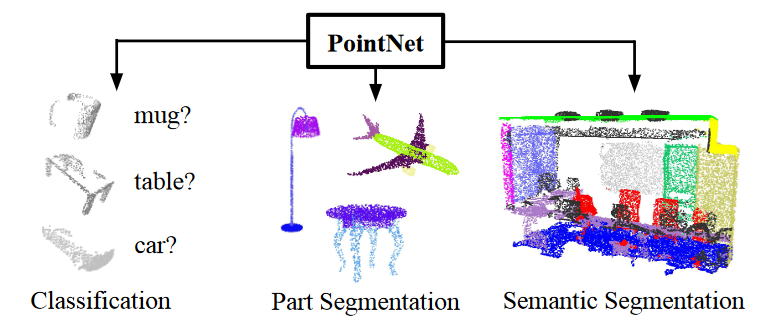
理论分析

点云存在两个问题

无序性

点云是一组无序的向量，其中点的不同排序，结果应该一致。

如何解决？

  • 方式一：按照一定规则对点集进行排序；
  • 方式二：将点集的所有排列作为增强数据，训练一个循环网络；
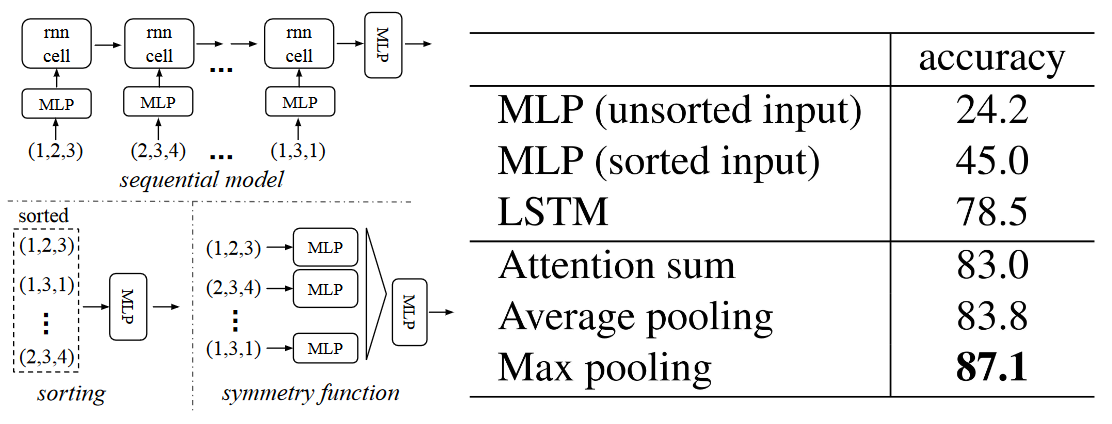
  • 方式三：利用一个对称函数将所有信息进行聚合；其中， 方式一看似简单，但是在高维空间中，实际上不存在一个在一般意义上相对于点扰动稳定的排序方式。 方式二被证明对于长度小的序列 (几十个) 有较好的鲁棒性，但对于动不动上千的点云数据不太合适。 因此，PointNet 采用方式三，具体三种方式的精度对比如下：

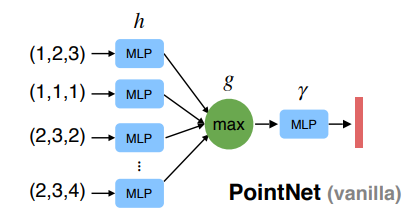
文章的主要思想是对集合中的变换元素应用对称函数来近似定义在点集上的通用函数： f(x1,...,xn)≈g(h(x1),...,h(xn)) 其中，h 函数使用 MLP 网络近似，g 函数使用 单变量函数与 MaxPool 函数的组合。

常见的对称函数有:

  • 求和函数 g(x1,x2,...,xn)=x1+x2+...+xn
  • 求最大值函数 g(x1,x2,...,xn)=max{x1,x2,...,xn} 通过一系列的 h 函数可以捕获点集合的不同属性 (3D 结构特征等) 故 PointNet 选择采用多层感知机 (MLP) 和最大池化 (MaxPool) 算子构建网络框架。

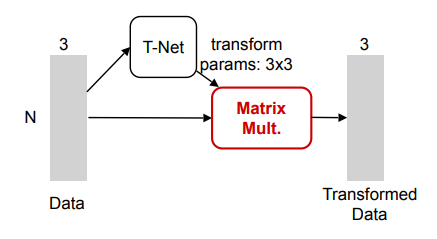
旋转变换后分类结果一致

要做到旋转的一致性，PointNet 引入 T-Net 得到一个旋转矩阵，对输入特征进行自动对齐。将正则化项添加到我们的 softmax 训练损失中，即将特征变换矩阵约束为接近正交矩阵（正交变换不会丢失输入中的信息）。

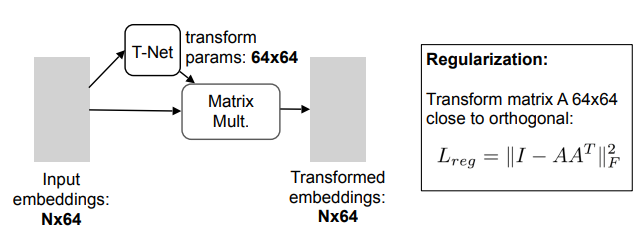
实验发现，通过添加正则化项，优化变得更加稳定，并且模型也获得了更好的性能。

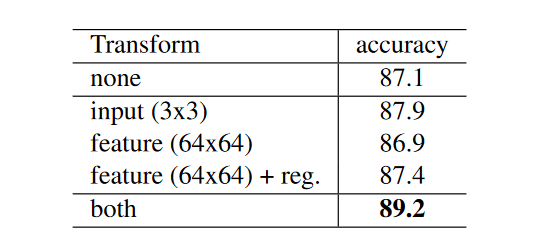
使用输入变换精度可以提升 0.8%，而增加正则损失对高维度的变换是有效的。

鲁棒性好

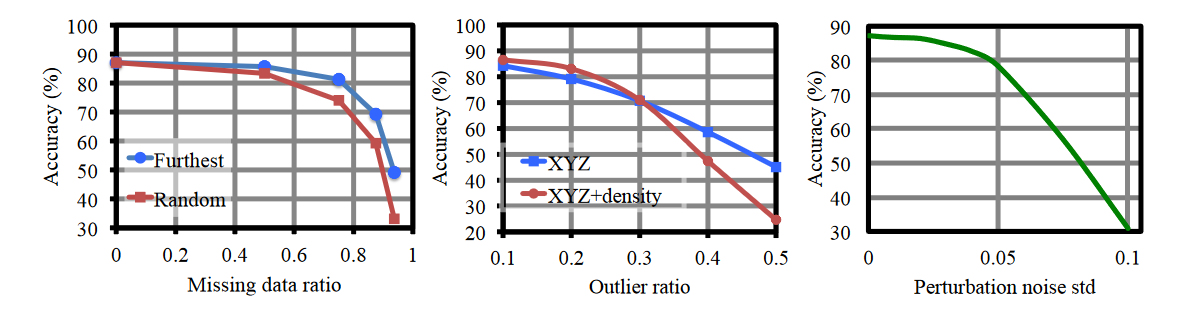
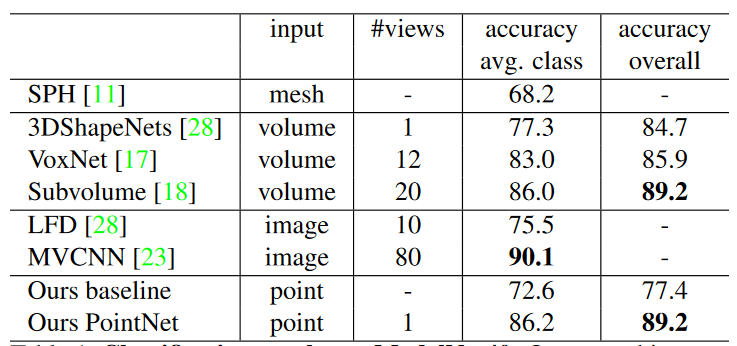
实验结果

网络结构

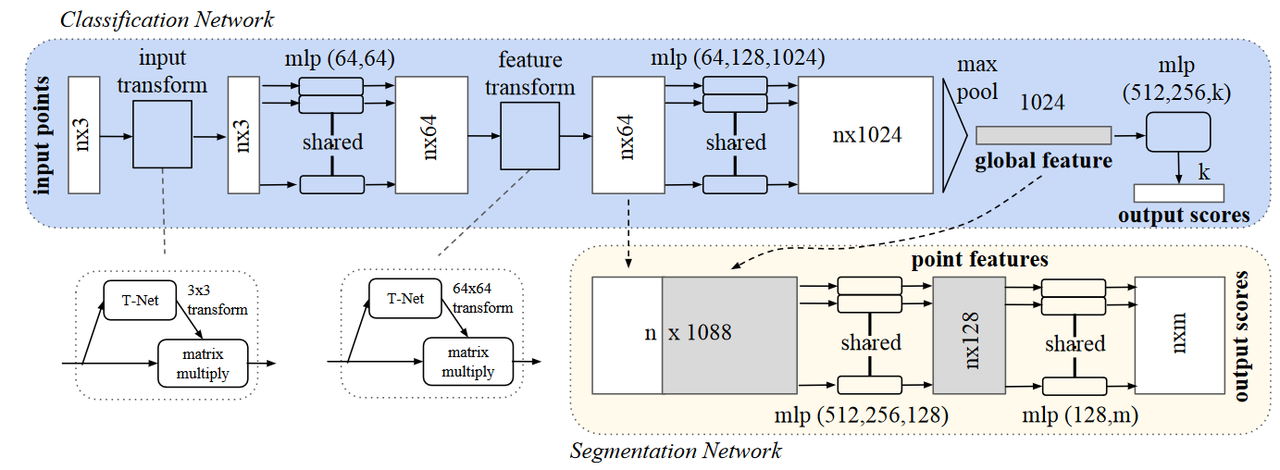
  • 分类网路只使用 global 特征进行预测；
  • 语义分割网络使用 local 和 global 特征进行预测；

Share MLP

PointNet 使用二维卷积网络来实现 Shared MLP。

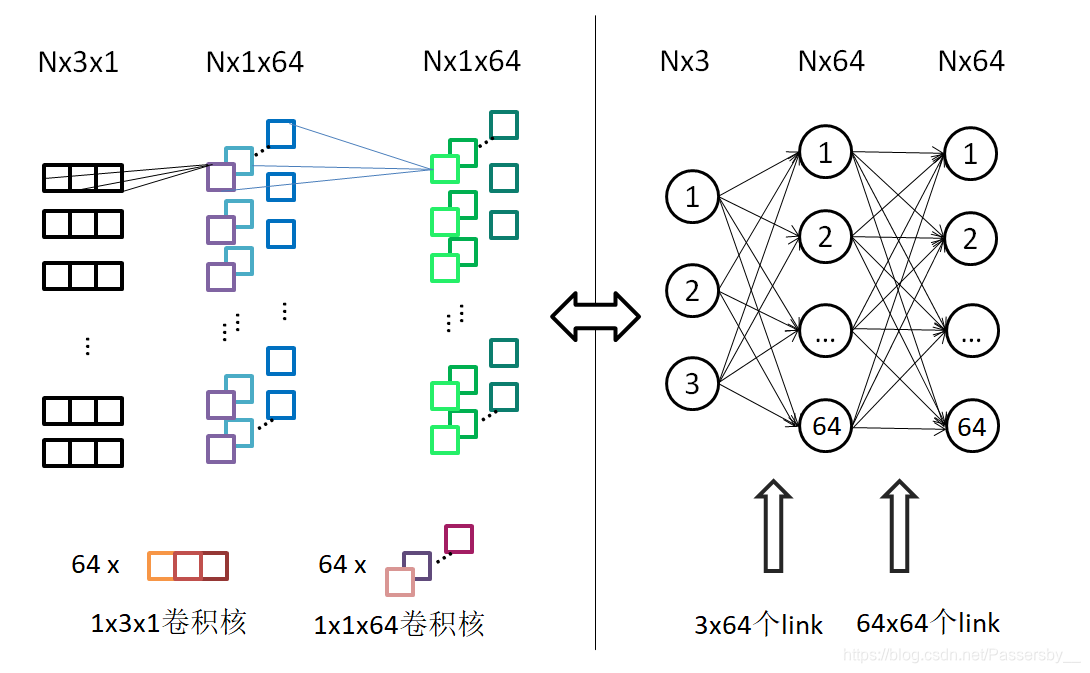
网络代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
def get_model(point_cloud, is_training, bn_decay=None):
    """ Classification PointNet, input is BxNx3, output Bx40 """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value
    end_points = {}

    with tf.variable_scope('transform_net1') as sc:
        transform = input_transform_net(point_cloud, is_training, bn_decay, K=3)
    point_cloud_transformed = tf.matmul(point_cloud, transform)
    input_image = tf.expand_dims(point_cloud_transformed, -1)

    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv2', bn_decay=bn_decay)

    with tf.variable_scope('transform_net2') as sc:
        transform = feature_transform_net(net, is_training, bn_decay, K=64)
    end_points['transform'] = transform
    net_transformed = tf.matmul(tf.squeeze(net, axis=[2]), transform)
    net_transformed = tf.expand_dims(net_transformed, [2])

    net = tf_util.conv2d(net_transformed, 64, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv3', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv4', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='conv5', bn_decay=bn_decay)

    # Symmetric function: max pooling
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='maxpool')

    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='fc1', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp1')
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='fc2', bn_decay=bn_decay)
    net = tf_util.dropout(net, keep_prob=0.7, is_training=is_training,
                          scope='dp2')
    net = tf_util.fully_connected(net, 40, activation_fn=None, scope='fc3')

    return net, end_points

T-Net

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
def input_transform_net(point_cloud, is_training, bn_decay=None, K=3):
    """ Input (XYZ) Transform Net, input is BxNx3 gray image
        Return:
            Transformation matrix of size 3xK """
    batch_size = point_cloud.get_shape()[0].value
    num_point = point_cloud.get_shape()[1].value

    input_image = tf.expand_dims(point_cloud, -1)
    net = tf_util.conv2d(input_image, 64, [1,3],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv1', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 128, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv2', bn_decay=bn_decay)
    net = tf_util.conv2d(net, 1024, [1,1],
                         padding='VALID', stride=[1,1],
                         bn=True, is_training=is_training,
                         scope='tconv3', bn_decay=bn_decay)
    net = tf_util.max_pool2d(net, [num_point,1],
                             padding='VALID', scope='tmaxpool')

    net = tf.reshape(net, [batch_size, -1])
    net = tf_util.fully_connected(net, 512, bn=True, is_training=is_training,
                                  scope='tfc1', bn_decay=bn_decay)
    net = tf_util.fully_connected(net, 256, bn=True, is_training=is_training,
                                  scope='tfc2', bn_decay=bn_decay)

    with tf.variable_scope('transform_XYZ') as sc:
        assert(K==3)
        weights = tf.get_variable('weights', [256, 3*K],
                                  initializer=tf.constant_initializer(0.0),
                                  dtype=tf.float32)
        biases = tf.get_variable('biases', [3*K],
                                 initializer=tf.constant_initializer(0.0),
                                 dtype=tf.float32)
        biases += tf.constant([1,0,0,0,1,0,0,0,1], dtype=tf.float32)
        transform = tf.matmul(net, weights)
        transform = tf.nn.bias_add(transform, biases)

    transform = tf.reshape(transform, [batch_size, 3, K])
    return transform