3D对象表示方法
概述

显性表示
体素

相对于2D对象表示使用像素,对应的3D表示可以使用体素表示,由若干个规则的立方体在三维空间中放置。为了表示三维物体的形状,体素中可以存储几何占有率、体积、密度和符号距离等信息,便于渲染。体素本身不包含位置信息,可以通过体素间的相对位置推导位置信息。
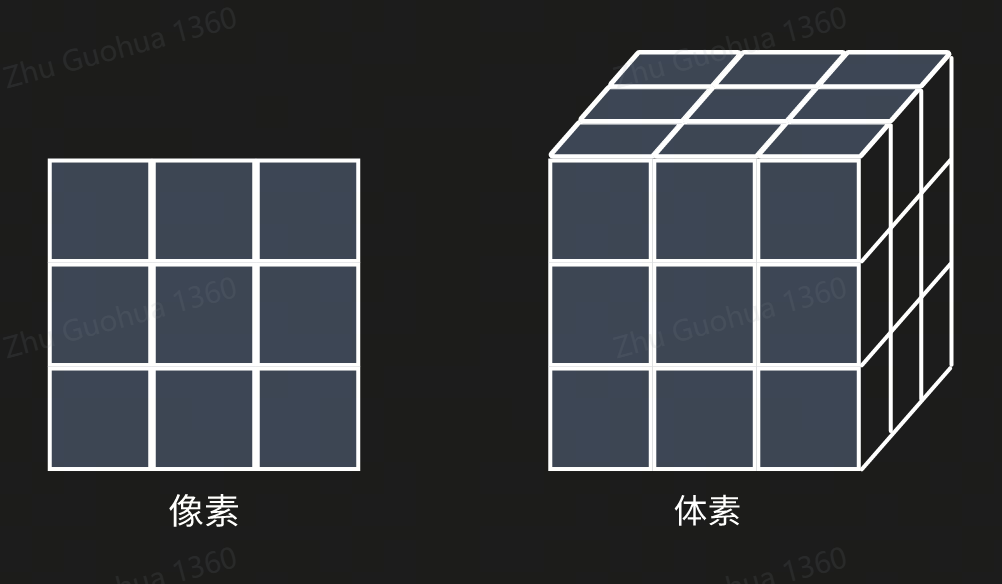
由于体素表示的规则性,可以配合标准的卷积神经网络。将三维几何物体表示为体素上二元变量的概率分布。 尽管体素网格非常适合3D卷积网络,但其通常内存效率低下,内存随着分辨率呈立方增加。
点云

多边形网格(Polygon Mesh)

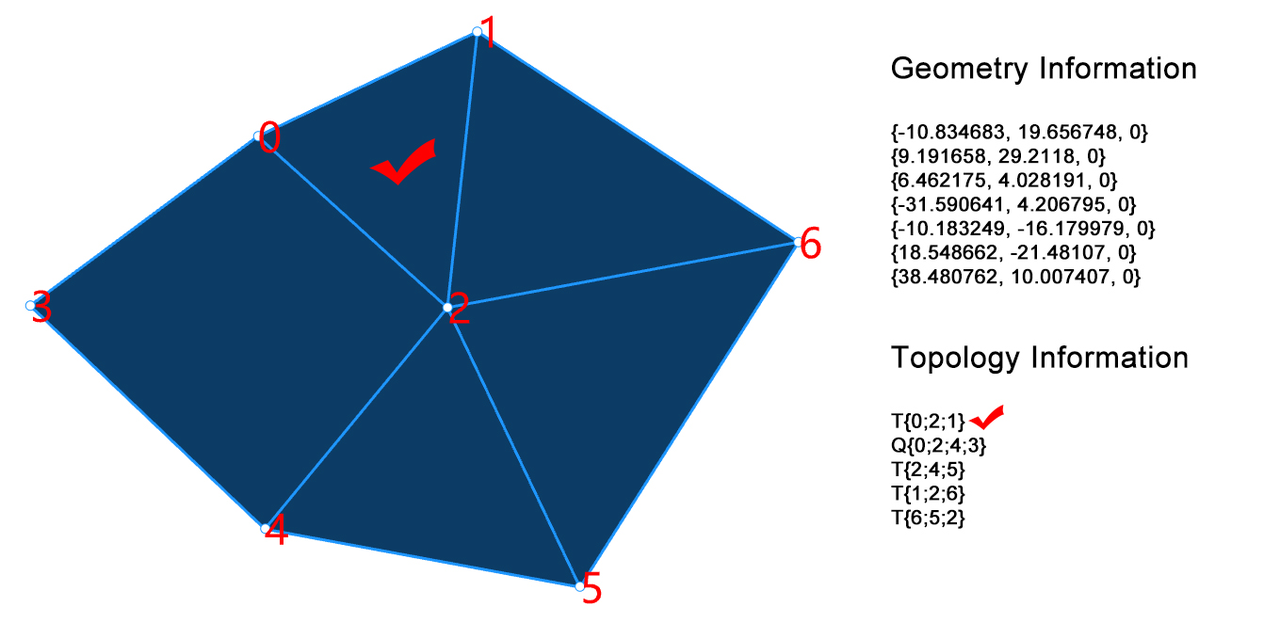
隐式表示
隐式表示是一种对各种信号进行参数化的新方法,传统的信号表示通常是离散的,而隐式表示将信号参数化为一个连续函数,将信号的域映射到该坐标上的属性的值,并且该函数通常不是可解析性的,即不可能学下将自然图像参数化为数学公式的函数。隐式表示通过神经网络来近似信号函数。
不与空间分辨率相耦合 例如,图像与像素数量相耦合的方式。隐式神经表示是连续函数,因此参数化信号所需的内存与空间分辨率无关,只与底层信号的复杂性相关。另一个推论是,隐式表示具有“无限分辨率”——它们可以在任意空间分辨率下进行采样。所以隐式表示解决了在显示表示中显存的限制,使得超分辨率成为可能;
表征能力更强 跨神经隐式表示的泛化等同于学习函数空间上的先验,通过学习神经网络权重上的先验实现。学习后的隐式表示可以通过不同的坐标输入映射到任意属性值。
泛化性高 神经隐式表示学习函数空间上的先验,然后根据提取的先验以及输入的特征,可以得到不同的目标信号。
易于学习 基于神经网络的隐式神经表示易于与各种网络结构结合,能够快速的学习先验,拟合学习对象。与传统的表示形式(如网格、点云或体素)相比,神经隐式表征可以灵活地融合到可微分的基于学习的管道中。
占用函数(Occupancy Function)
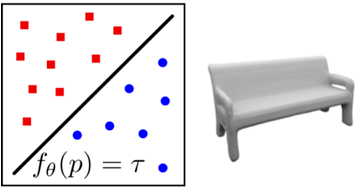
符号距离函数(Singned Distance Function)
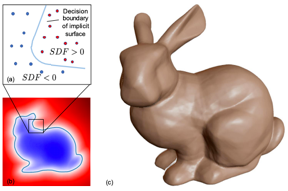
如果大家对隐式表示感兴趣,后续会做详细的论文解读。