碰撞检测-apollo
概述
本文主要分析aplollo代码中关于障碍物碰撞检测相关算法,该算法通过将车辆抽象成二维矩形盒(Box),建立点与矩形盒、线段与矩形盒、矩形盒与矩形盒的碰撞检测算法。

碰撞判断
点与矩形盒
关于点与矩形盒子的位置关系,可能情况为点在矩形盒内,点在矩形边框上和点在矩形盒外部,如果点在矩形盒的外部,可以求取点到矩形盒的距离值.
判定点是否在矩形盒内
如下图所示,红色圆点与矩形盒的关系如下图左侧,为了便于判定红点是否在矩形盒内,将下图左侧整体按照航向角顺时针旋转\(\theta\)角度,得到下图右侧状态.此时,只需要判定红点的坐标\((dx,dy)\)是否满足\(\mid dx \mid <= length_h\) 或者 \(\mid dy \mid <= width_h\),则说明红点位于矩形盒内.
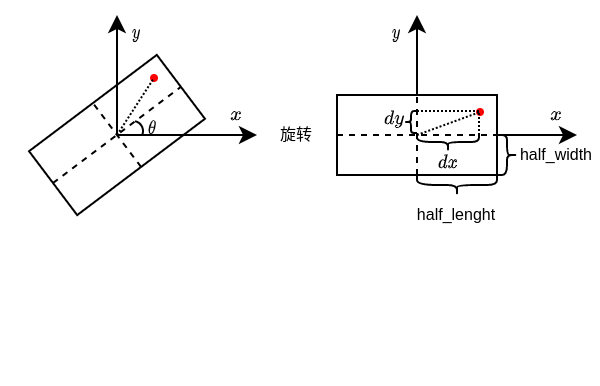
其中,
- \(length_{half}\): 车长的一半;
- \(width_{half}\): 车宽的一半;
判定点是否在矩形盒边界上
如下图所示,当红点位于矩形盒的边界上时,先以航向角顺时针旋转\(\theta\)角度,然后通过判断旋转后的红点坐标\((dx,dy)\)是否满足\(\mid \mid dx \mid - length_h \mid == 0\) 或者 \(\mid \mid dy \mid - width_h \mid == 0\),则说明点红点位于矩形盒边界上.
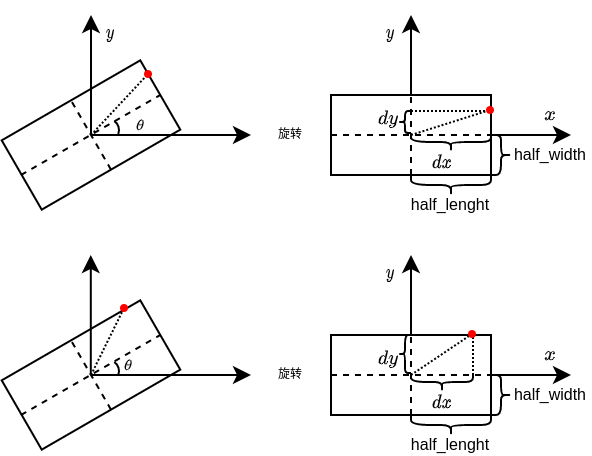
其中,
- \(length_{half}\): 车长的一半;
- \(width_{half}\): 车宽的一半;
计算点到矩形盒的距离
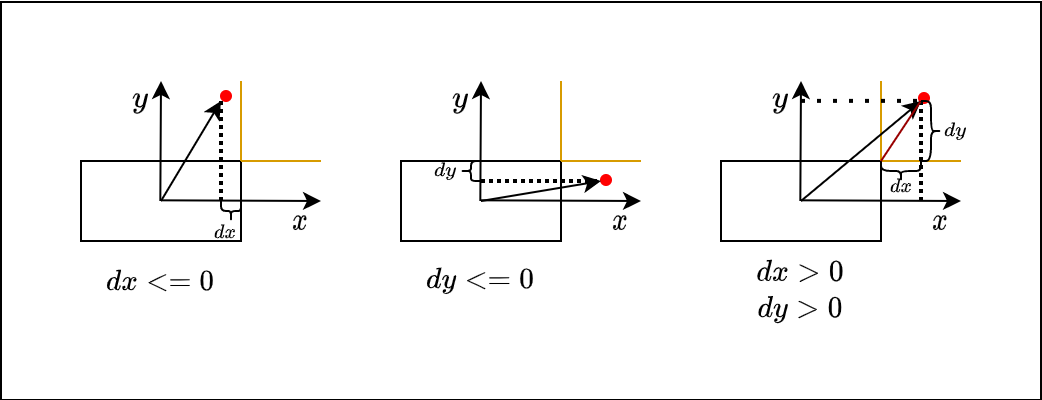
如下图所示,点到矩形盒的距离可以分为如下三种情况:
dx <= 0:如果红点在\(x\)轴上的投影小于等于车长距离的一半,则此时的距离可以表示为\(\mid dy \mid\);dy <= 0:如果条件1不满足,即dx > 0,则判断红点在\(y\)轴上的投影是否小于等于车宽的一半,如果满足条件,则距离可以表示为\(\mid dx \mid\);dx > 0 and dy > 0: 如果条件1和2都不满足,则距离可以表示为红点与矩形盒边角点的距离,即\(\sqrt{dx^2 + dy^2}\);
线段与矩形盒
判定线段与矩形盒是否交叠
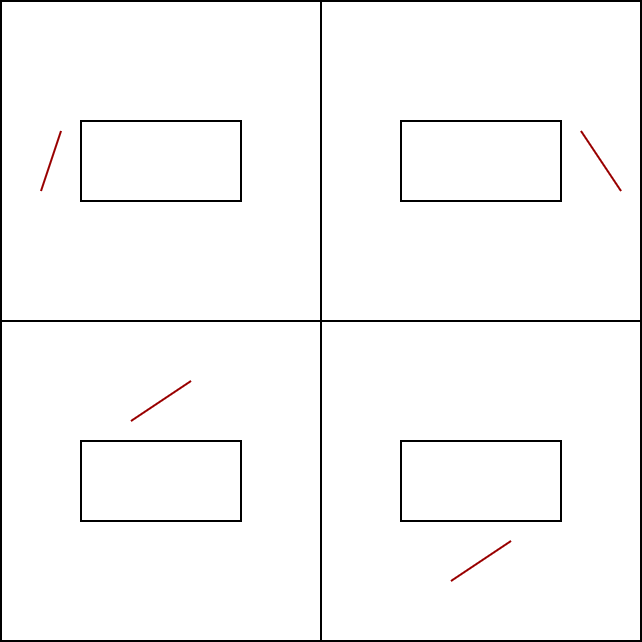
关于某线段与矩形盒关系的判定,先计算线段的长度,如果线段的长度为0,则可以把该线段当作一个点,利用点和矩形盒的距离来判断是否交叠;如果线段的长度不为0,则先进行线段与矩形盒的粗判定,即线段的起始点与终点是否落在矩形盒的一边,如下图所示,表示线段位于矩形盒一边的四种情况.如果线段不满足如下关系,则交叠关系可以通过距离来判断.
计算线段到矩形盒的距离
区域划分
如下图所示,将矩形盒的外围分成如下8个区域,关于区域的划分,可以根据线段起始点和终点分别在\(x\)轴和\(y\)轴的投影,表示为\((p_x,p_y)\);以车辆中心\(o\)为原点,则四个边角点可以表示为\((box_x,box_y)\),\((box_x,-box_y)\),\((-box_x,box_y)\),\((-box_x,-box_y)\).
其中,根据点在\(x\)轴的投影,可以将区域值表示如下:
\[ g_x=\begin{cases} 1 & \text{if } (p_x >= box_x),\\ 0 & \text{if } (-box_x < p_x < box_x),\\ -1 & \text{if } (p_x <= -box_x),\\ \end{cases} \]
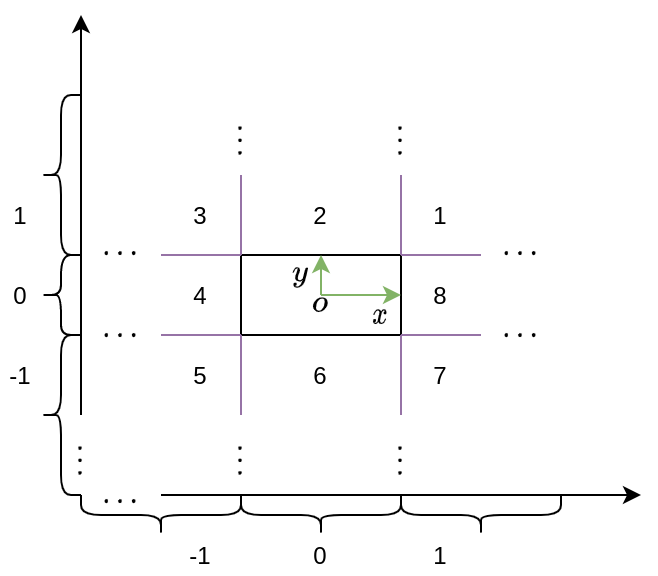
根据上图,区域的值表示如下:
| 区域 | gx | gy |
|---|---|---|
| 1 | 1 | 1 |
| 2 | 0 | 1 |
| 3 | -1 | 1 |
| 4 | -1 | 0 |
| 5 | -1 | -1 |
| 6 | 0 | -1 |
| 7 | 1 | -1 |
| 8 | 1 | 0 |
其中,区域\((0,0)\)位于矩形盒内,即线段中有一点位于矩形盒内,必定与矩形盒交叠.因此去除点位于区域\((0,0)\)的情形,考虑线段两个端点与矩形盒的关系共有\(8 \times 8 = 64\)种情况.
对称变换
首先将起始点通过\(x\)轴和\(y\)轴对称变换,将落在区域3,4,5,6,7的点变换到区域1,2,8中.对于区域2和8,进行\(xy\)轴对称变换,将区域2变换为区域8.所以经过三种轴对称转换后,起始点将会落在区域1和区域8两种区域状态.
- 区域1
当起始点位于区域1,则将终点进行\(xy\)轴对称变换,将位于区域2,3,4的终点,对称变换到区域8,7,6中.因此关于终点的所在区域的情况只需考虑落在区域1,8,7,6,5,这五个区域的情况;
- 区域8
当起始点位于区域8,对终点进行\(y\)轴对称变换,将位于\(y\)轴下方的区域变换到\(y\)轴上方,即区域5,6,7对称变换到区域3,2,1.因此终点只需考虑区域8,1,2,3,4五个区域的请况.
通过上述对称变换,可以将原先的64种线段与矩形的关系减少到10种,从而减少相关计算量.
线段与矩形盒距离计算
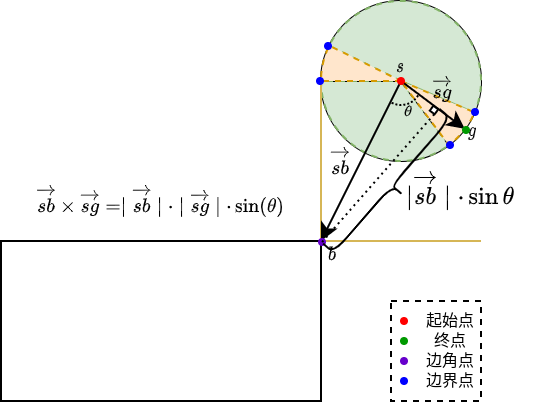
如下图所示,线段起始点与矩形盒边角点之间的向量表示为\(\vec{sb}\),起始点与终点之间的向量表示为\(\vec{sg}\).
- 当\(\vec{sb}\cdot\vec{sg} <= 0\)时,即下图浅绿色表示的区域,此时,线段与矩形盒的距离表示为\(\mid \vec{sb}\mid\).
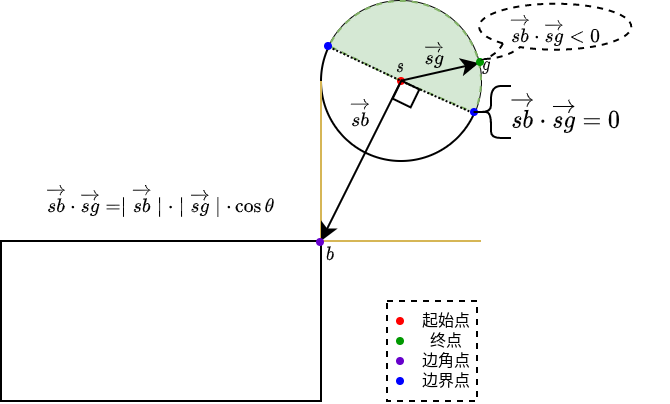
- 当\(\vec{sb}\cdot\vec{sg} >= \vec{sg} \cdot \vec{sg}\),即下图浅绿色区域,线段与矩形盒的距离可以表示为\(\mid \vec{sb}-\vec{sg}\mid\).
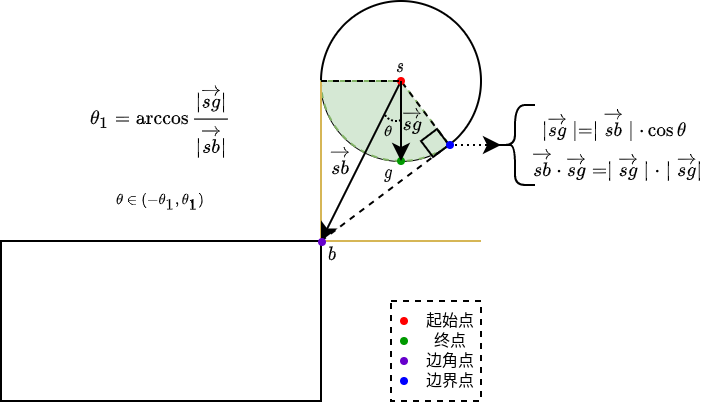
- 当上述条件都不满足时,即位于下图浅黄色区域,线段与矩形盒的距离可以表示为\(\mid \vec{sb} \mid \sin{\theta}\),可使用向量叉乘得到\(\frac{\vec{sb}\times\vec{sg}}{\mid \vec{sg} \mid}\).
起始点区域1
- 当终点位于区域1时,直接使用上述方法计算距离值;
- 当终点位于区域8时,先判定起始点与终点的\(x\)轴坐标的关系,当起始点坐标的\(x\)轴坐标大于终点的\(x\)轴坐标,则距离值为\(\mid g_x - b_x \mid\),否则按照上述方法计算距离值;
- 当终点位于区域7时,先判定起始点与终点的\(x\)轴坐标的关系,选取不同的矩形盒的边角点;
- 当终点位于区域6时,先判定线段与矩形盒是否交叠,如下图所示,通过计算向量叉乘\(\vec{sg}\times\vec{sb}\),判断线段是否与矩形盒交叠.
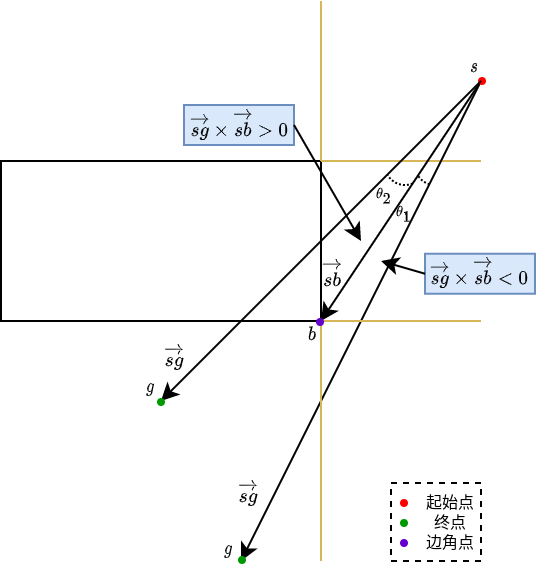
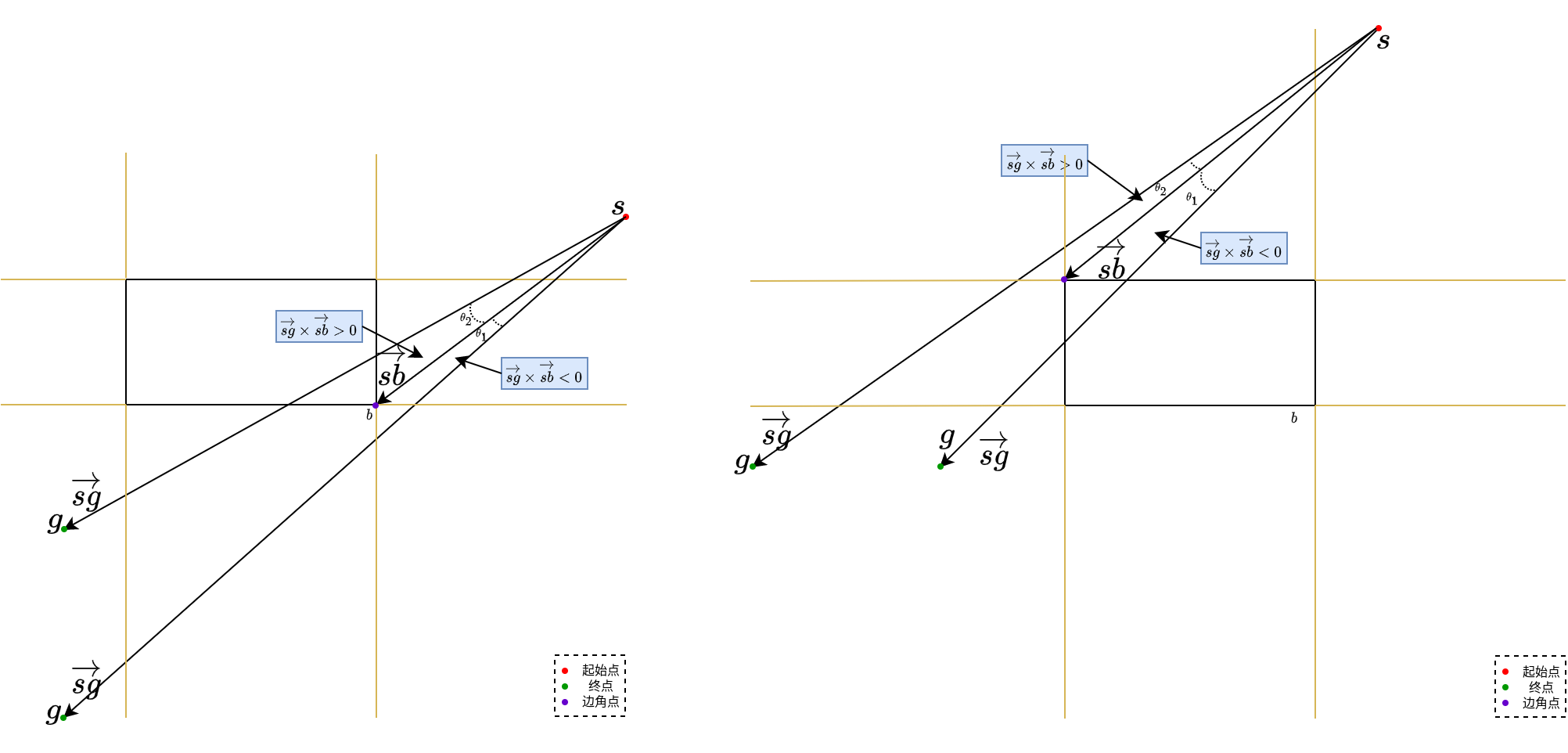
- 当终点位于区域5时,矩形盒的边角点分两种,首先判断与右下角的边角点的关系,如果不交叠则直接按上述方法计算距离值,否则判断与左上角边角点的关系,如果无交叠则按上述方法计算距离值.
起始点区域8
- 当终点位于区域1时,如下图所示,先判定起始点与终点的\(x\)轴坐标的关系,如果起始点小于终点,则距离值为\(\mid s_x - b_x \mid\),否则计算线段与矩形盒的距离;
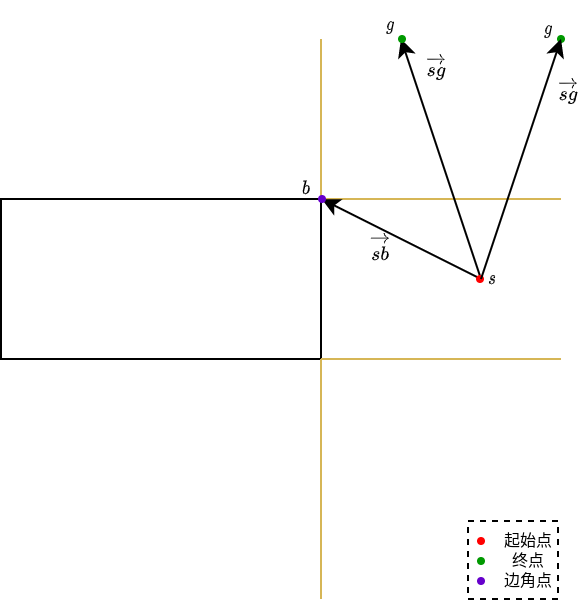
当终点位于区域8时,选取起始点与终点中离矩形盒最近的点到矩形盒的距离,即\(\mid min(s_x,g_x) -b_x \mid\);
当终点位于区域2和3时,如下图所示,通过右上边角点与线段的起始点,终点形成的矢量,进行矢量叉乘,通过数值的正负判断线段是否与矩形盒交叠;
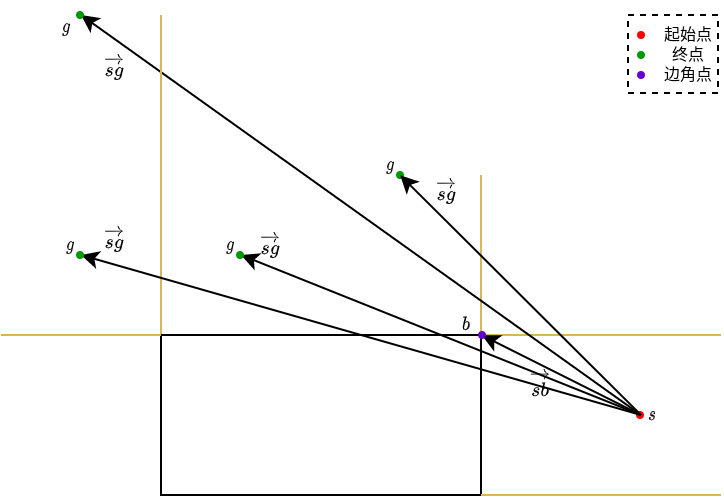
- 当终点位于区域4时,线段与矩形盒一定交叠;
矩形盒与矩形盒
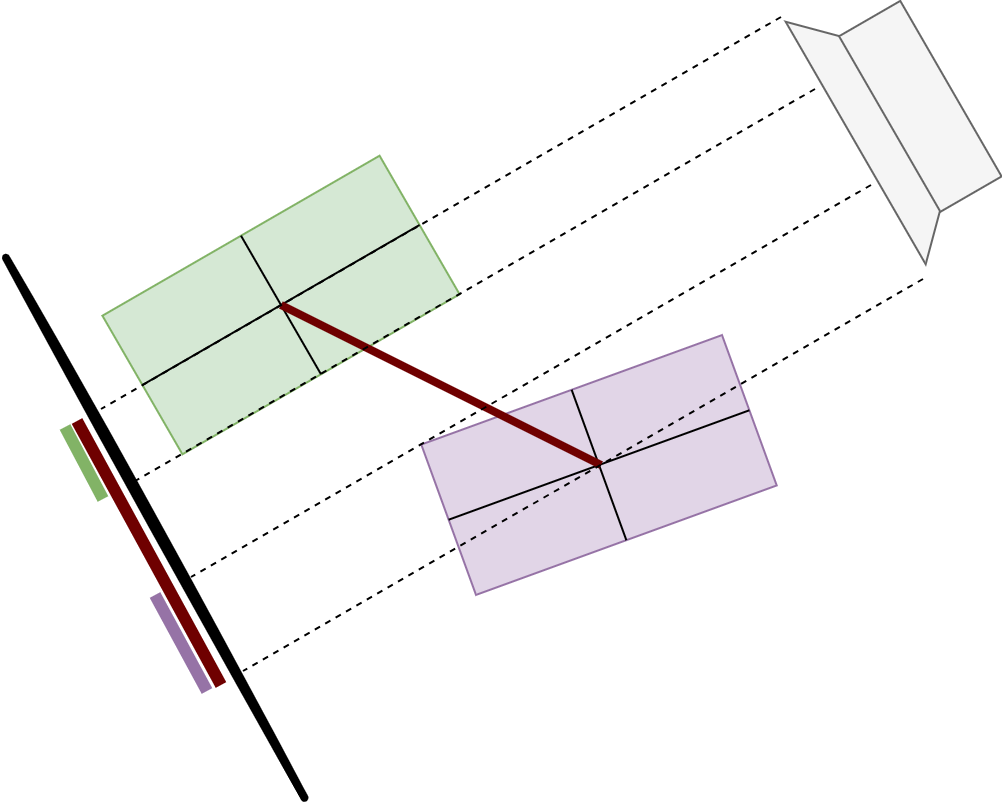
关于矩形盒与矩形盒的碰撞检测采用分离轴原理,即通过判断任意两个凸多边形在任意角度下的投影是否均存在重叠,来判断是否发生碰撞。若在某一角度光源下,两物体的投影存在间隙,则为不碰撞,否则为发生碰撞。 如下图所示,将左右两个矩形盒投影到左侧矩形盒长边所在轴上,从图中可以看出投影重叠;
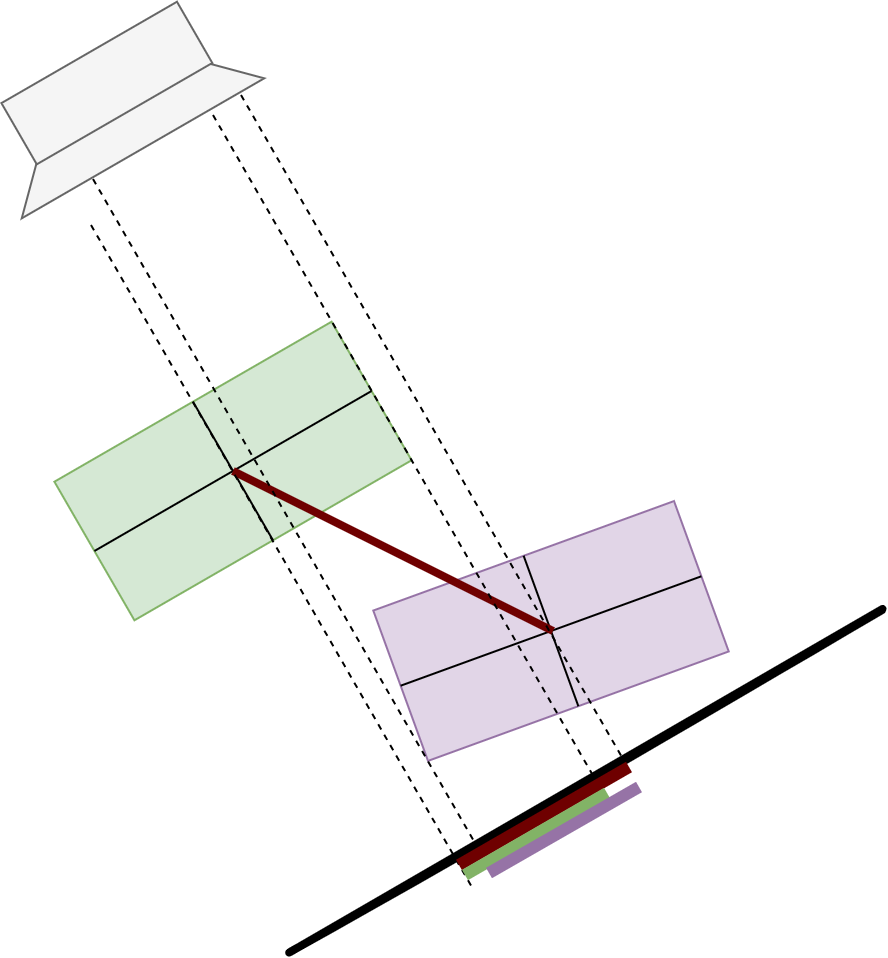
如下图所示,以左侧矩形盒短边为轴,将矩形盒投影到该轴上,可以发现投影无重叠,只要存在一种投影方式无重叠,则说明无碰撞。