控制算法-后轮位置反馈
概述
本文介绍一种使用后轮位置反馈的路径跟踪算法,使用李亚普洛夫稳定判据,推导控制率。

误差
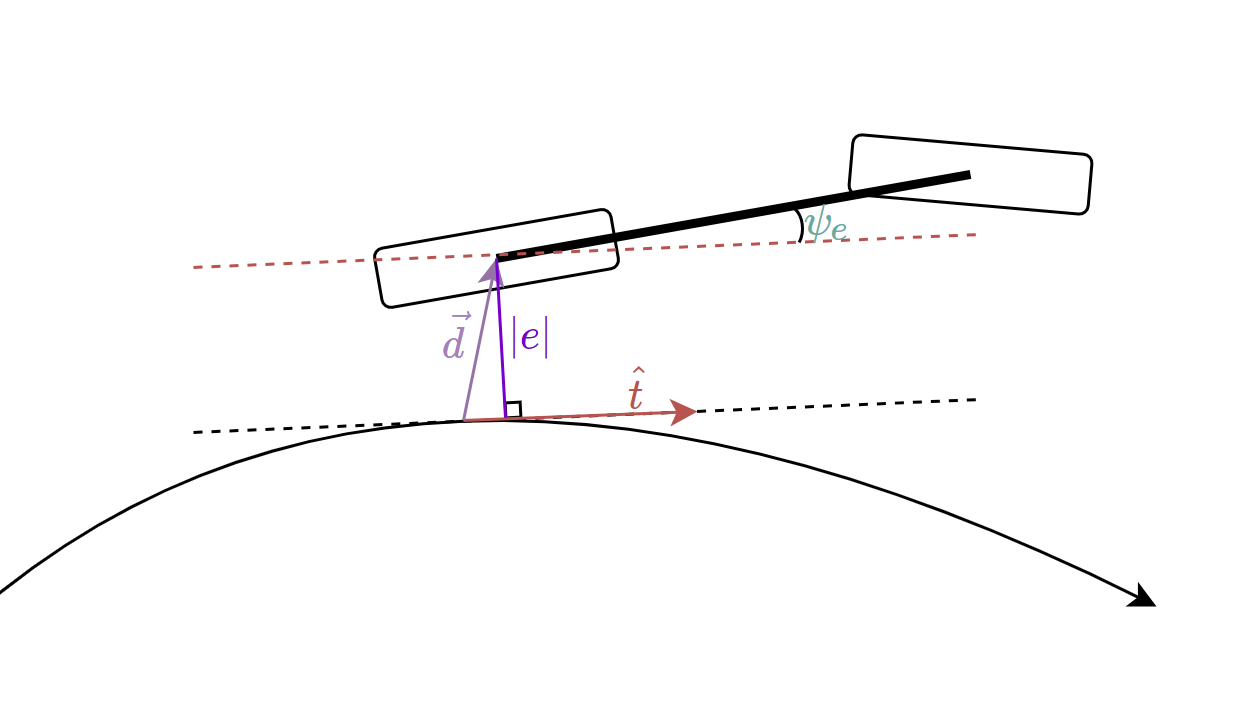
位置误差
关于位置误差的计算,首先搜寻参考路径与车辆后轴中心距离最近的点:
\[ s(t) = arg\min_{\gamma}\|\bigl(x_r(t),y_r(t)\bigr)-\bigl(x_{ref}(\gamma),y_{ref}(\gamma)\bigr) \| \tag{1} \]
其中,\(\bigl(x_r(t),y_r(t)\bigr)\)代表\(t\)时刻车辆后轴中心位置坐标,\(\bigl(x_{ref}(\gamma),y_{ref}(\gamma)\bigr)\)代表参考路径上离车辆后轴距离最近点的位置坐标,\(s(t)\)代表\(t\)时刻与车辆后轴中心点距离最近参考路径点的位置参数\(\gamma\)。
关于参考路径在\(s(t)\)参数处的单位切向量为
\[ \hat{t}= \frac{ \Bigl(\dfrac{\partial x_{ref}}{\partial s}\|_{s(t)},\dfrac{\partial y_{ref}}{ \partial s}\|_{s(t)} \Bigr)} {\Bigg\| \Bigl(\dfrac{ \partial x_{ref}\bigl(s(t)\bigr)}{ \partial s},\dfrac{ \partial y_{ref}\bigl(s(t)\bigr)}{ \partial s}\Bigr) \Biggr\|} =(t_x,t_y) \tag{2} \]
跟踪误差向量表示如下:
\[ \vec{d}(t)=\Bigl(x_r(t) - x_{ref}\bigl(s(t)\bigr),y_r(t) - y_{ref}\bigl(s(t)\bigr)\Bigr)=(d_x,d_y)\tag{3} \]
所以跟踪误差向量\(\vec{d}\)和参考路径上最近点的单位切向量\(\hat{t}\)的向量积为
\[ \vec{e} = \hat{t} \times \vec{d} = \left\lvert \begin{array}{cl} x & y\\ t_x & t_y\\ d_x & d_y \end{array} \right\rvert=t_xd_y - t_yd_x \tag{4} \]
角度误差
关于车辆航向向量与目标路径切向量的夹角\(\psi_e\)如下:
\[ \psi_e(t)=\psi-\arctan2(\frac{ \partial y_{ref}\bigl(s(t)\bigr)}{ \partial s},\frac{ \partial x_{ref}\bigl(s(t)\bigr)}{ \partial s}) \tag{5} \]
微分方程
参考曲线最近点
关于参考曲线与车辆后轴中心最近点处的速度\(\dot{s}(t)\)可以通过下图求得
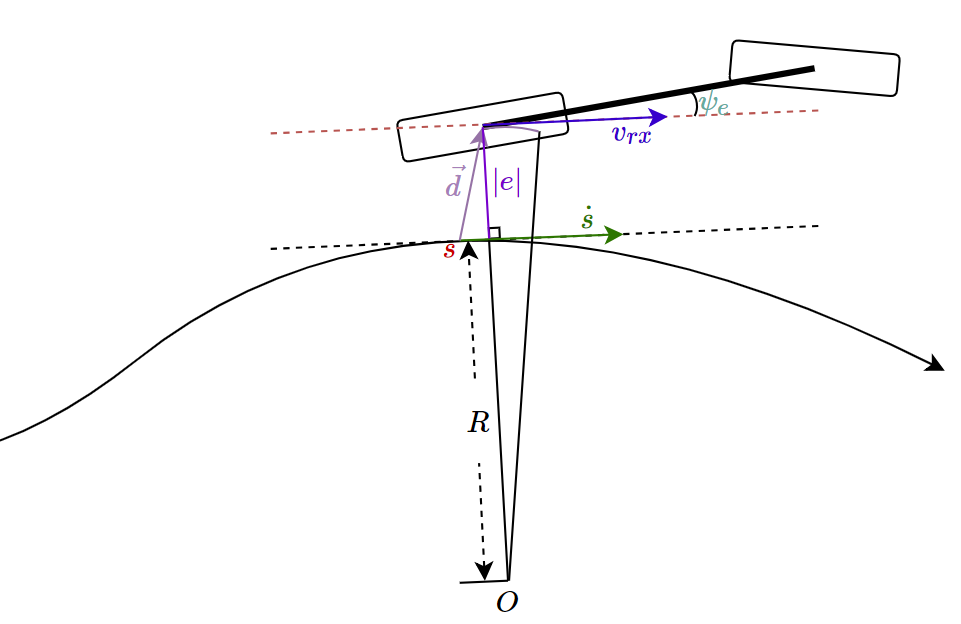
如上图所示,车辆沿目标路径顺时针运动,点\(O\)代表当前目标曲线点对应的旋转中心。很明显此时曲率为负值,即\(R < 0\)。根据矢量叉乘性质得,\(e > 0\)。假设以点\(O\)为旋转中心的车辆后轴中心角速度\(\omega_r\)和最近参考路径点处的角速度\(\omega_s\)近似相等,得
\[ \omega_r = \omega_s < 0\tag{6} \]
根据车辆旋转角速度的计算等式\(\frac{V}{R}\),结合等式(6)得
\[ \frac{v_{rx}}{R-e} = \frac{\dot{s}}{R} \tag{7} \]
故\(\dot{s}\)结果如下
\[ \dot{s} = \frac{R \cdot v_{rx}}{R - e}=\frac{v_{r}\cdot\cos(\psi_e)}{1-k(s)e}\tag{8} \]
横向误差
车辆横向移动的速度\(\dot{e}\)可以表示如下:
\[ \dot{e} = v_r \cdot \sin(\psi_e)\tag{9} \]
航向角误差
关于车辆航向角误差的变化率表示如下:
\[ \begin{array}{cl} \dot{\psi_e} &= \dot{\psi} - \dot{\psi_{ref}} \\ &= \dot{\psi} - \dot{s}\cdot k(s)\\ &=\dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} \end{array}\tag{10} \]
综述
基于上述参考曲线处的速度、横向误差变化率和航向角误差变化率,整理如下微分方程形式:
\[ \begin{array}{cl} \dot{s} &= \dfrac{v_{r}\cdot\cos(\psi_e)}{1-k(s)e}\\ \dot{e} &= v_r \cdot \sin(\psi_e)\\ \dot{\psi_e} &=\dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} \end{array}\tag{11} \]
李亚普洛夫稳定判据
Lyapunov函数
基于上述微分方程,定义李亚普洛夫函数形式如下:
\[ V(e,\psi_e) = \frac{1}{2}e^2 + \frac{1}{2k_2}\psi_e^2 \tag{12} \]
其中\(k_2 > 0\),为了使\((e,\psi_e)\)在平衡点\((0,0)\)处稳定,根据李亚普洛夫稳定判据,必须满足一下两个条件:
- \(\lim_{\rvert e,\psi_e \rvert \to \infty}V = \infty\)
- \(\begin{array}{rl}\dot{V} < 0 &(e \neq 0,\psi_e \neq 0)\end{array}\)
对于条件1,等式(12)明显成立,所以李亚普洛夫稳定判据第一条满足。
对于\(\dot{V}\),结合等式(11)的微分方程,推导形式如下:
\[ \begin{array}{cl} \dot{V} &= e\dot{e} + \dfrac{1}{k_2}\psi_e\dot{\psi}_e\\ &=e \cdot v_r \cdot \sin(\psi_e) + \dfrac{1}{k_2}\psi_e\Bigl(\dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e}\Bigr) \end{array}\tag{13} \]
根据等式(13),另\(\dot{V} = 0\),得
\[ \begin{array}{cl} v_r \cdot \sin(\psi_e)\cdot e + \dfrac{1}{k_2}\psi_e\Bigl(\dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e}\Bigr)=0\\ k_2 v_r \dfrac{\sin(\psi_e)}{\psi_e}e + \dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} = 0\\ \end{array} \tag{14} \]
求出零界控制率\(\dot{\psi_e}\) 如下:
\[ \dot{\psi}^* = \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} - k_2 v_r \dfrac{\sin(\psi_e)}{\psi_e}e \tag{15} \]
为了满足第2条李亚普洛夫稳定判据,设置一个调节函数\(g(e, \psi_e, t) > 0\),可以得出基于航向角变化率的控制命令:
\[ \dot{\psi} = \dot{\psi}^* - g(e,\psi_e,t)\psi_e\tag{16} \]
设置\(g(e,{\psi}_e,t)= k_{\psi}|v_r|\) ,其中\(k_{\psi} > 0\)。
\[ \dot{\psi} = \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} - k_2 v_r \dfrac{\sin(\psi_e)}{\psi_e}e - k_{\psi}|v_r|\psi_e \tag{17} \]
将等式(17)带入等式(13)得
\[ \begin{array}{cl} \dot{V} &=v_r \cdot \sin(\psi_e) \cdot e + \dfrac{1}{k_2}\psi_e\Bigl(\dot{\psi} - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e}\Bigr)\\ &=v_r \cdot \sin(\psi_e) \cdot e +\dfrac{1}{k_2}\psi_e\bigl(- k_2 v_r \dfrac{\sin(\psi_e)}{\psi_e}e - k_{\psi}|v_r|\psi_e\bigr)\\ &=v_r \cdot \sin(\psi_e) \cdot e - v_r \cdot \sin(\psi_e) \cdot e -\dfrac{k_{\psi}}{k_2}|v_r|\psi_e^2\\ &=-\dfrac{k_{\psi}}{k_2}|v_r|\psi_e^2 \leq 0 \end{array}\tag{18} \]
所以设计得控制率满足稳定性条件。
控制率
根据车辆几何关系
\[ \tan(\delta) = \frac{L}{R} \tag{19} \]
车辆航向变化率与车速和转弯半径的关系为\(\dot{\psi} = \frac{V}{R}\),结合等式(17)可得
\[ \tan(\delta) = \frac{\dot{\psi}L}{V} \tag{20} \]
所以控制率\(\delta\)为
\[ \delta = \arctan(\frac{\dot{\psi}L}{v_r})\tag{21} \]
仿真
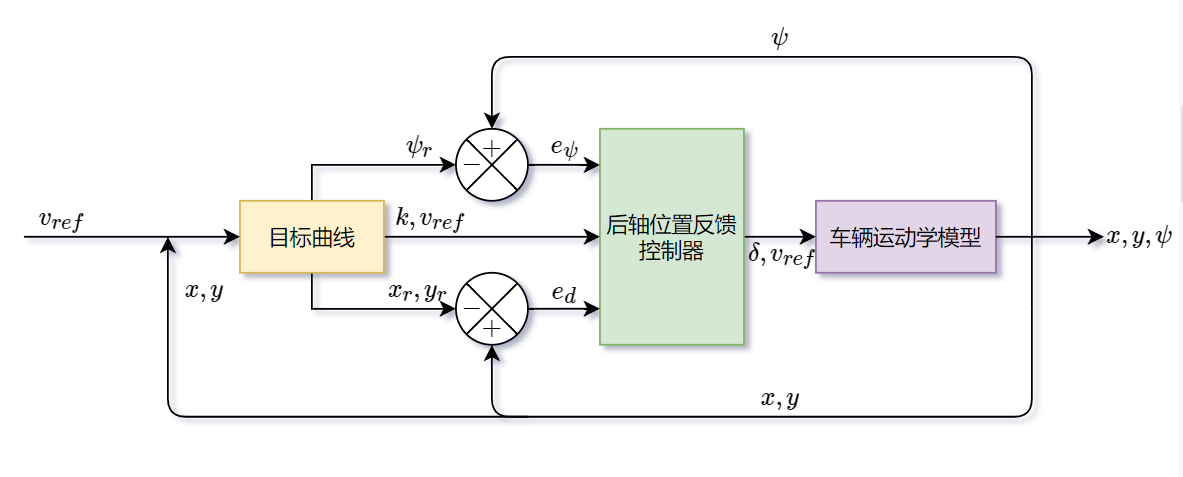
根据上述控制系统框图,搭建仿真环境,分别测试三角函数曲线和圆弧曲线的跟踪效果。
三角函数曲线跟踪
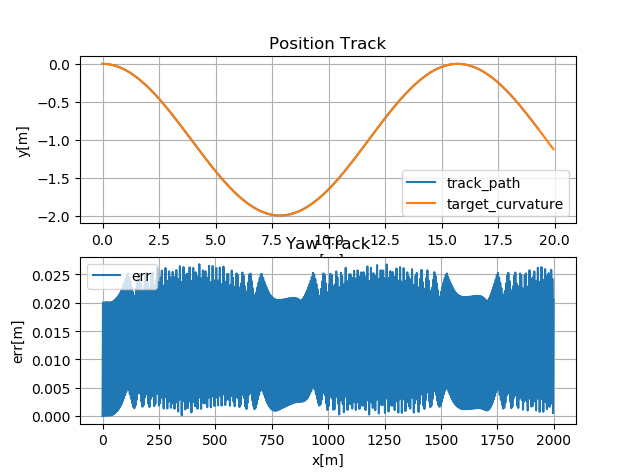
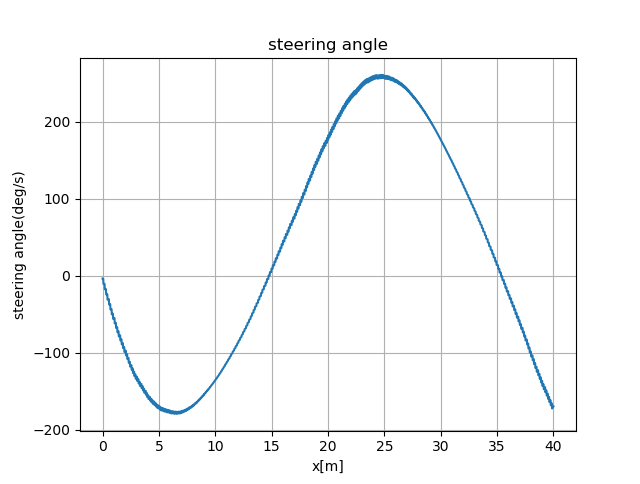
圆弧曲线跟踪
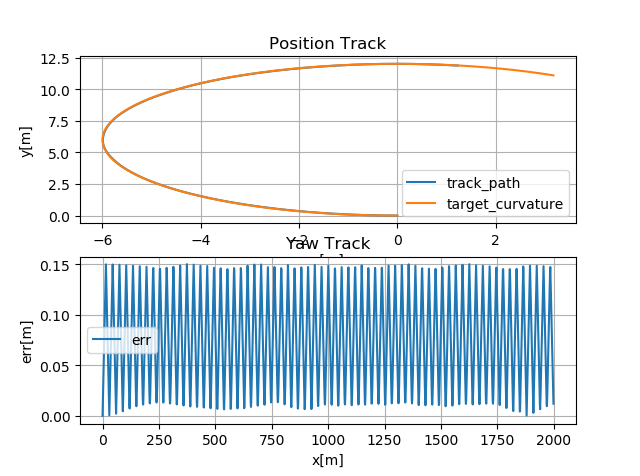
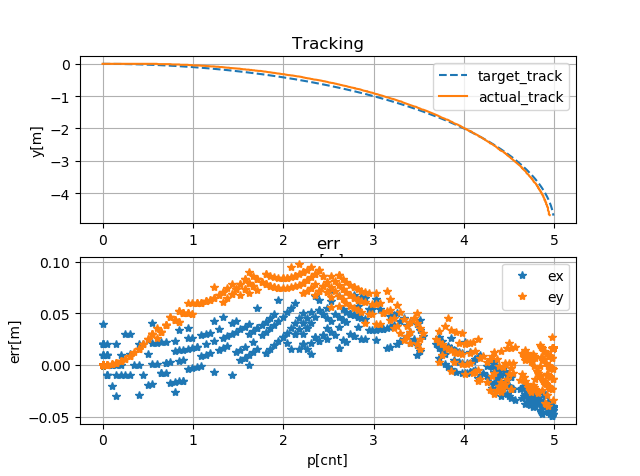
实测数据
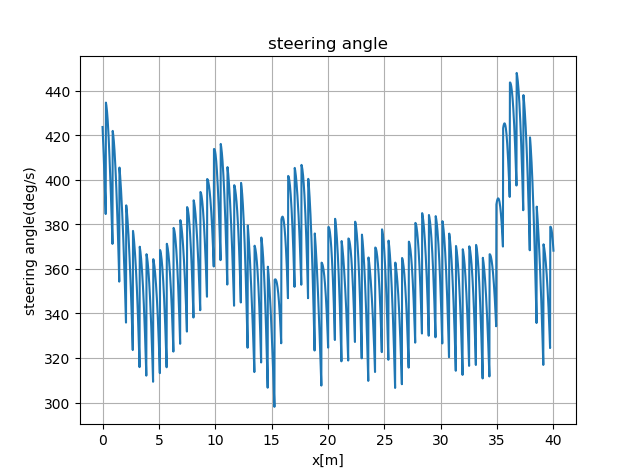
下图是实际车辆测试结果,测试条件如下:
- 初始位置(0,0),初始偏航角0°
- 目标位置(5,-5),目标偏航角-90°
- 初始转向角0°
- 初始速度0.5m/s
- 跟踪圆弧曲率-0.2
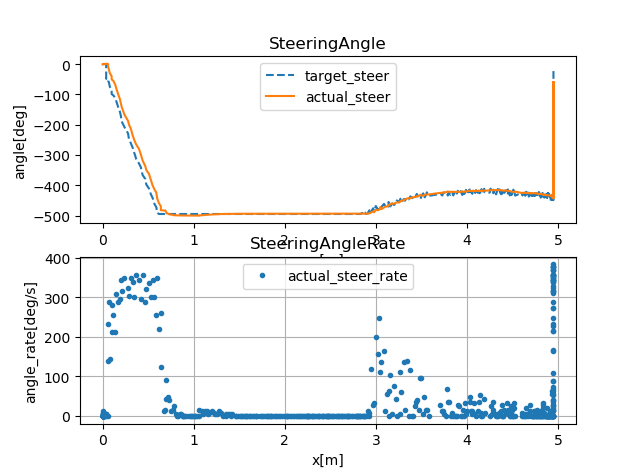
基于上图可知,跟踪过程主要分为三个阶段:
- 第一阶段(0,0.7)m:车辆按最大角速度转到右转最大角度500°左右
- 第二阶段(0.7,3)m:车辆保持最大转向角趋近于跟踪曲线
- 第三阶段(3,5)m:车辆跟踪目标曲线,按照控制率输出转向角
总结
后轴位置反馈控制对于曲率连续变化的曲线控制较好,但对于曲率恒定的曲线(圆弧),控制输出存在抖动。实际车辆控制时,由于执行器本身可以等效为一个低通滤波器,实测控制抖动较小。