控制算法-Stanley法
概述
本文主要介绍Stanley方法的推导,该方法也称为前轮位置反馈。该方法基于车辆几何关系,算法简单,适合低速下的车辆路劲跟踪。

Stanley方法
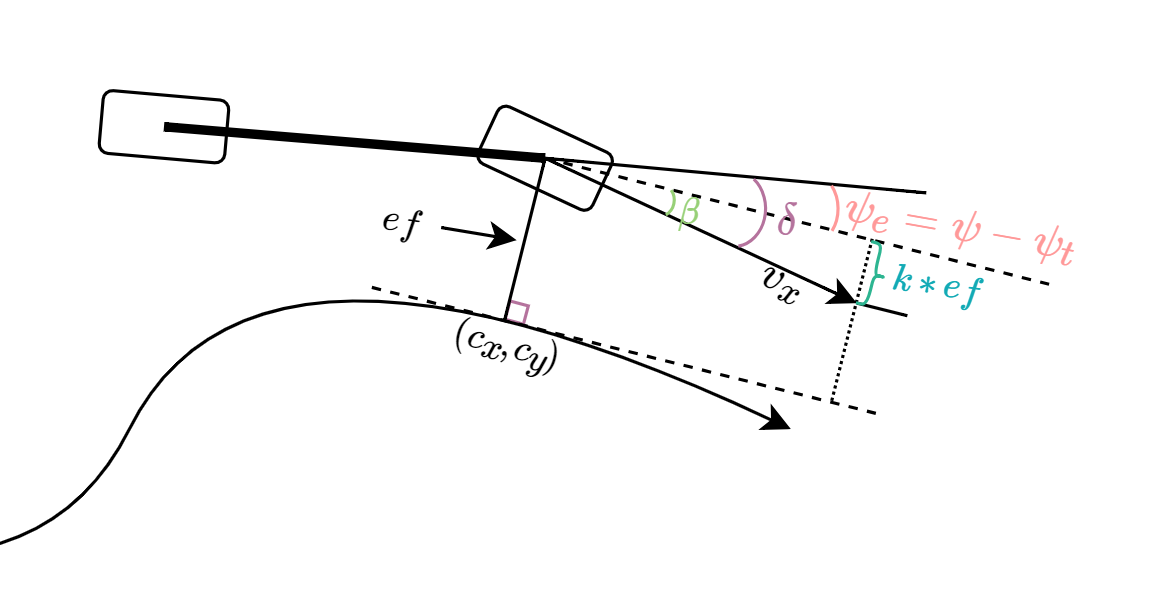
Stanley方法是一种基于航迹误差\(e_{f}\)的非线性反馈函数,该航向误差是车辆前轴中心点与目标路径最近点\((c_x,c_y)\)的距离。由上图几何关系得
\[ \psi_e = \psi - \psi_{t} \tag{1} \]
其中,\(\psi\)表示车辆横向角,\(\psi_{t}\)表示离车辆前轴中心最近目标路径点处的航向角。
前轮速度轴与目标路径航向之间的夹角\(\beta\)为
\[ \beta = \arcsin(\frac{k\cdot e_{f}}{v_x}) \tag{2} \]
但是在论文中都是使用反正切函数求\(\beta\)角,可能原因是系数\(k\)可以任意选择,选择可是的系数\(k\),确实可以转化为
\[ \beta = \arctan(\frac{k\cdot e_{f}}{v_x}) \tag{3} \]
结合等式(1)和(3)得
\[ \begin{array}{cl} \delta &= \psi_e + \beta \\ &= \psi - \psi_{t} + \arctan(\dfrac{k\cdot e_{f}}{v_x}) \end{array}\tag{4} \]