控制算法-路径跟踪
概述
本文介绍常见几种路径跟踪算法,并分析各自的优势。目前主要分为基于几何关系控制设计和基于模型的控制设计。其中几何关系可以分为,纯追踪算法、前轴反馈和后轴反馈算法。基于模型可以分为运动模型和动力学模型,控制算法可以使用LQR优化或者使用MPC。

基于几何关系设计
纯追踪算法
待补充
前轴反馈
前轴反馈控制也就是常说的Stanley方法,几何关系如下:
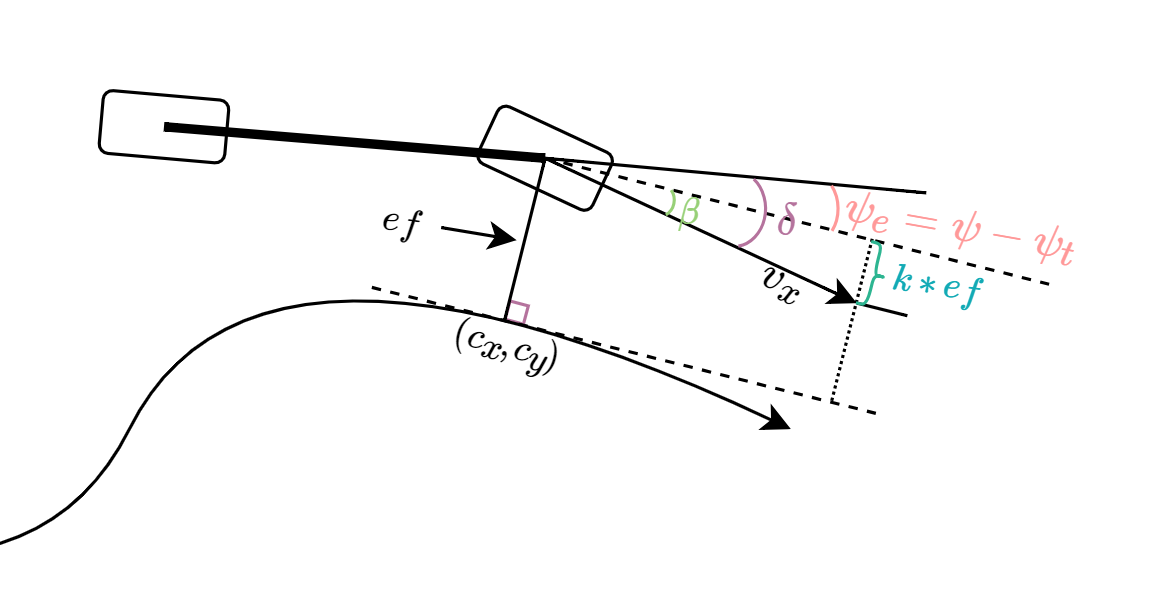
三角函数曲线跟踪
圆弧跟踪
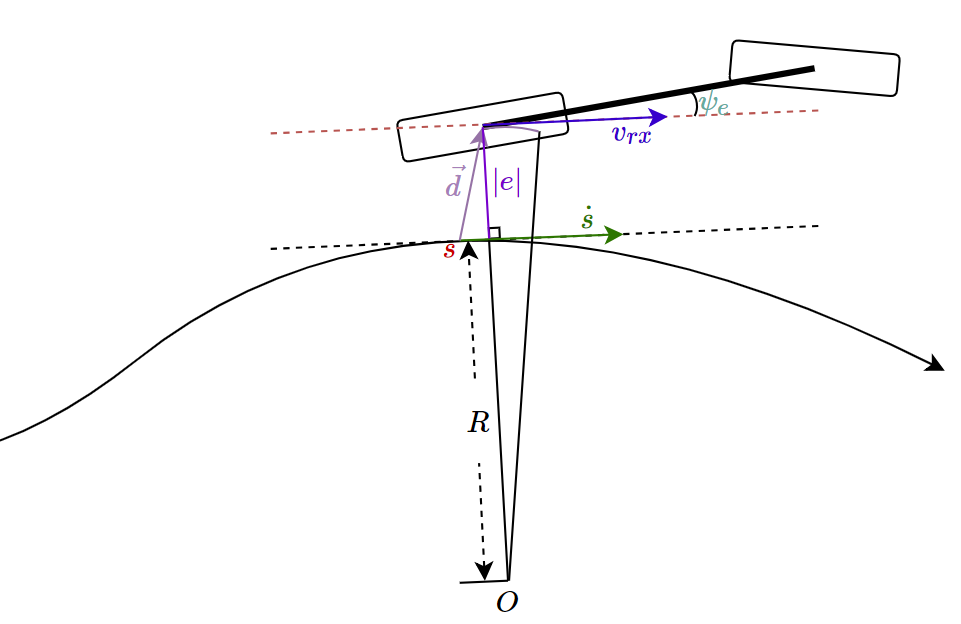
后轴反馈
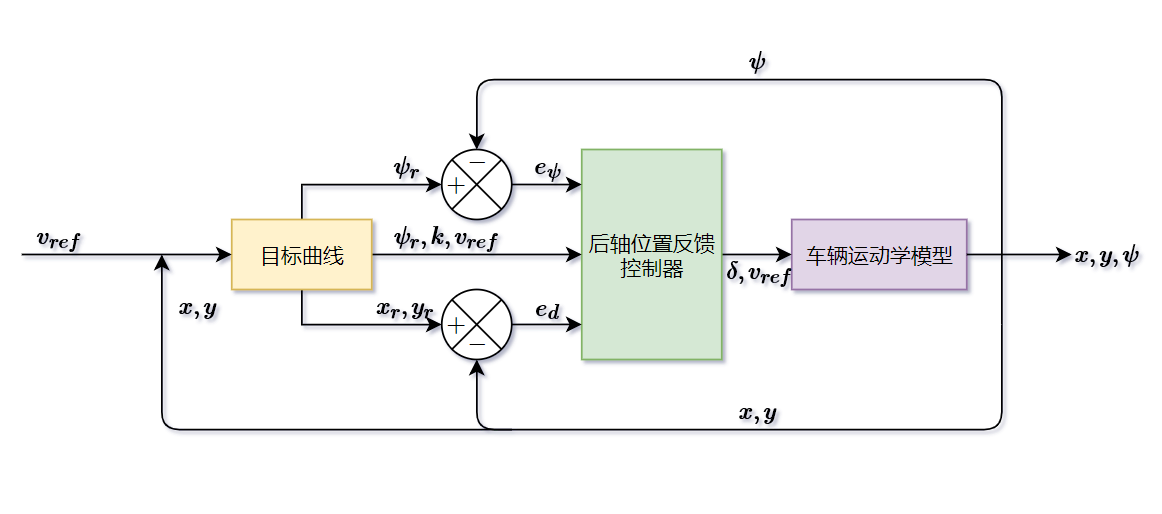
仿真系统框图
基于下图框图,搭建仿真环境,仿真条件如下:
- 仿真周期20ms
- 目标曲线采样间隔 5
- 初始位置(0,0)
- 初始偏航角0度
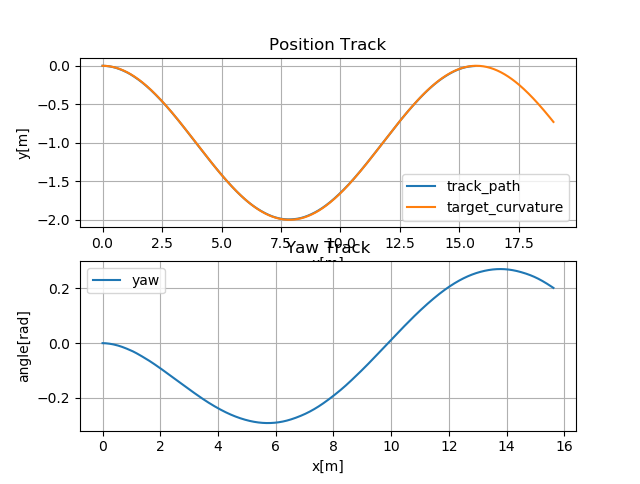
余弦曲线跟踪
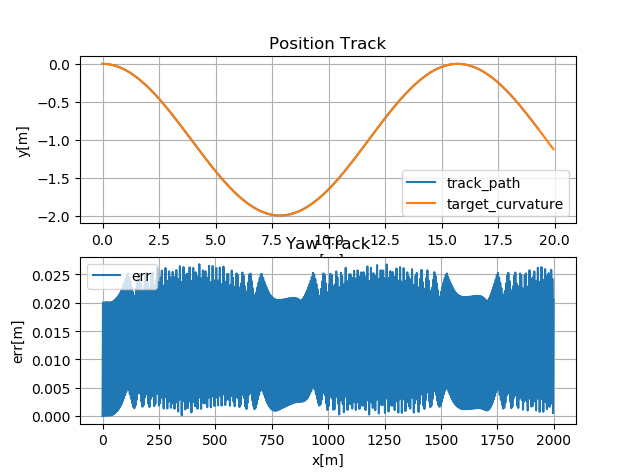
由上图可知,对于曲率连续变化的跟踪效果较好。

输出控制抖动也较小。
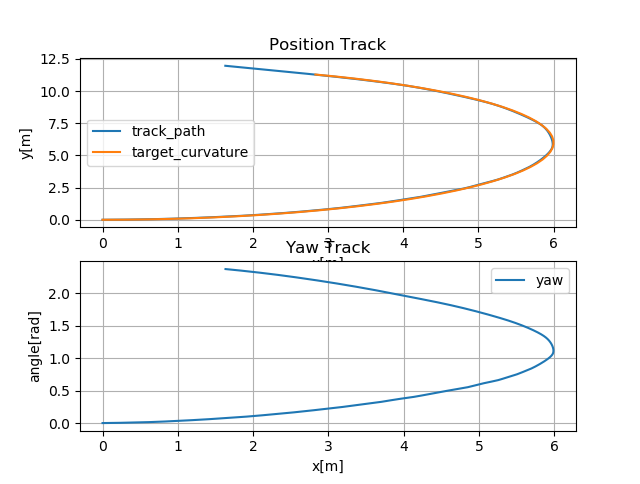
圆弧跟踪
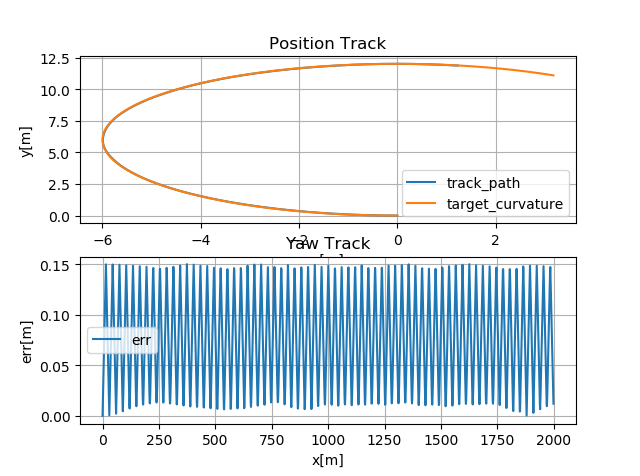
由上图可知,对于曲率恒定的圆弧曲线,控制效果较差,存在较大的位置偏差。
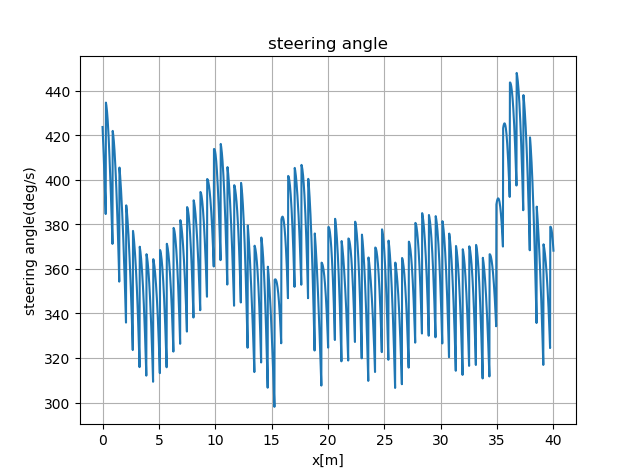
由上图可知,控制率震荡较大。
C++仿真效果
仿真条件:
- 初始位置为\[(0,0)\]
- 初始偏航角为\[0\]度
- 仿真周期20ms
- 目标曲线采样间隔 1
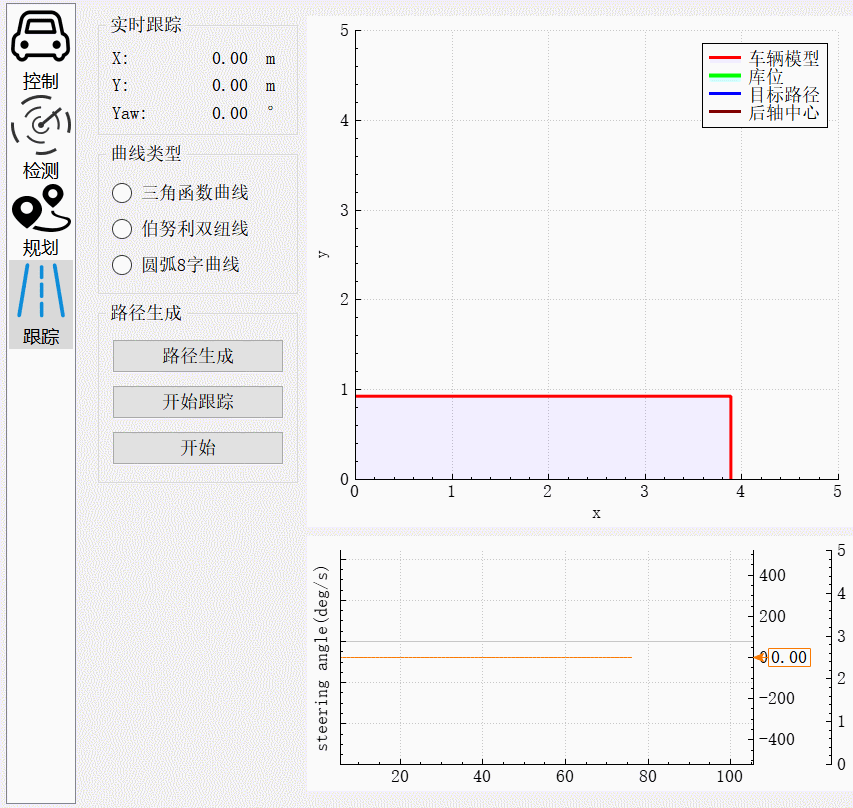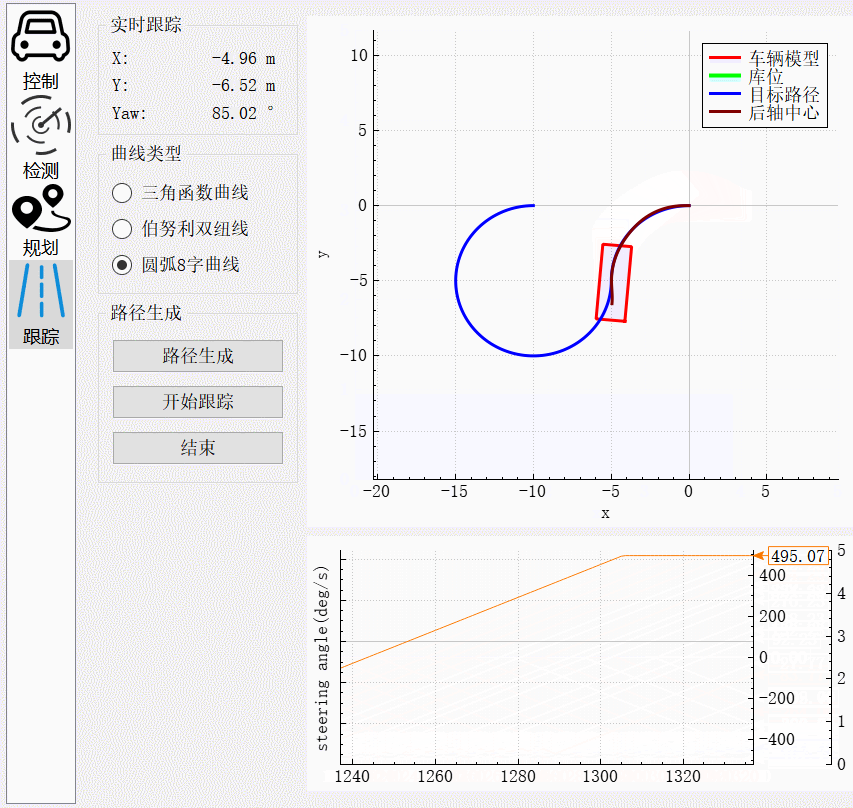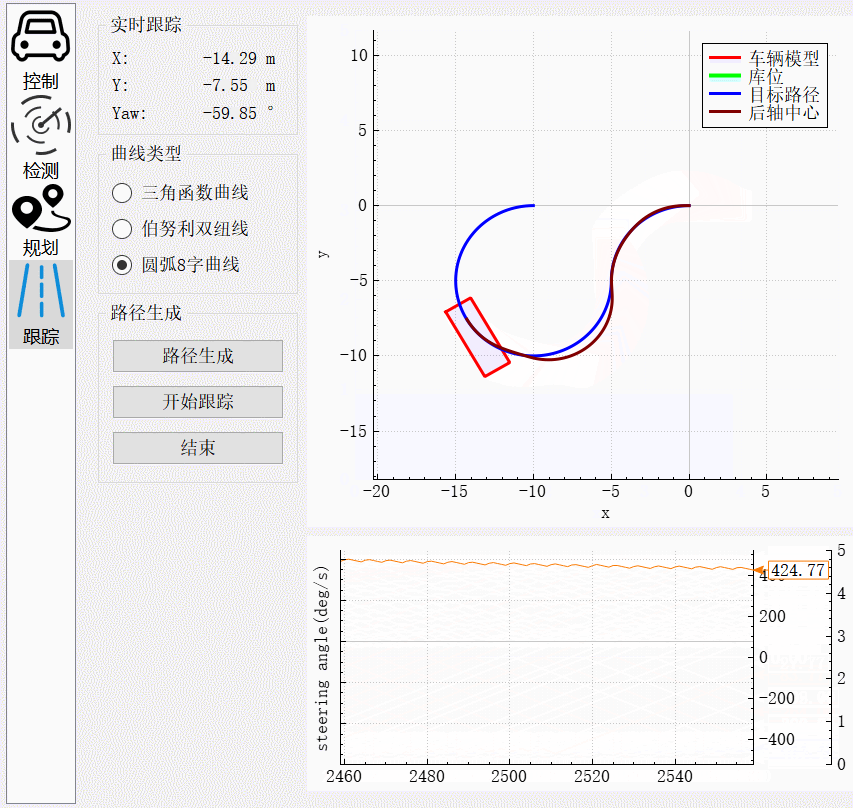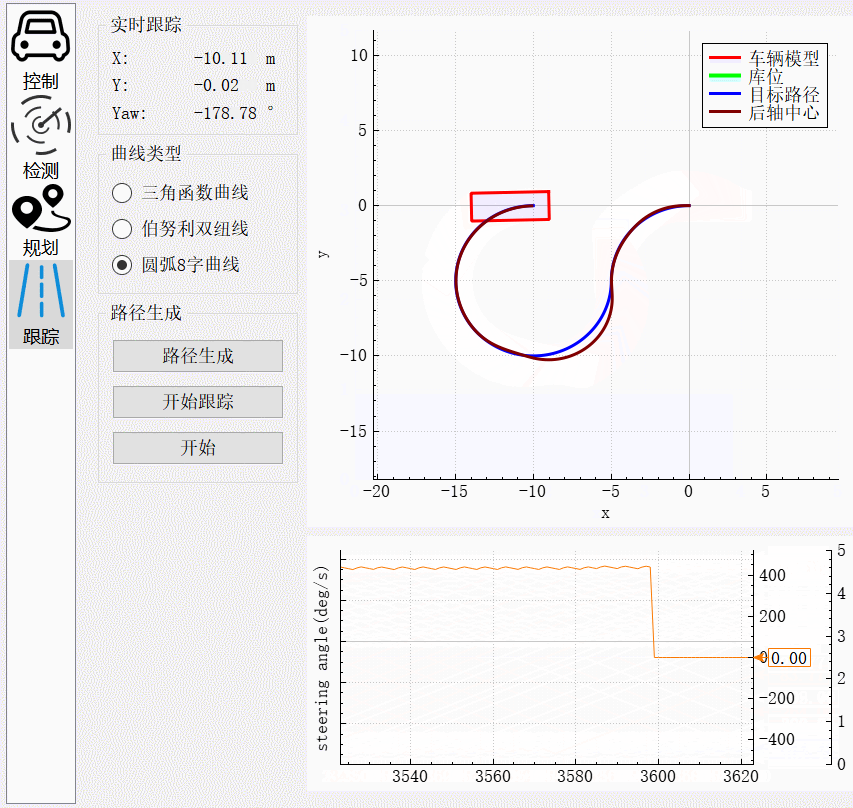
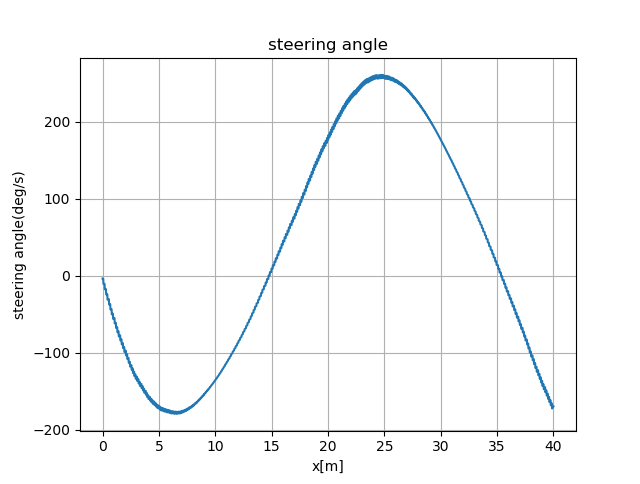
车辆刚起步时,由于输出转向角为0,而此时的圆弧曲率为-0.2,所以存在一段转向角按照最大角速度转到目标转向角的过程。跟踪过程中,从图中转向角的振荡幅度存在小范围的变化。在两个圆弧的交界处,由于曲率由-0.2突变到0.2,方向盘转向角需要按照最大角速度转到目标角度。在该过程中存在较大误差,但是在角度达到目标角度后,误差逐渐缩小,最后完全跟踪上目标曲线。
圆弧前进
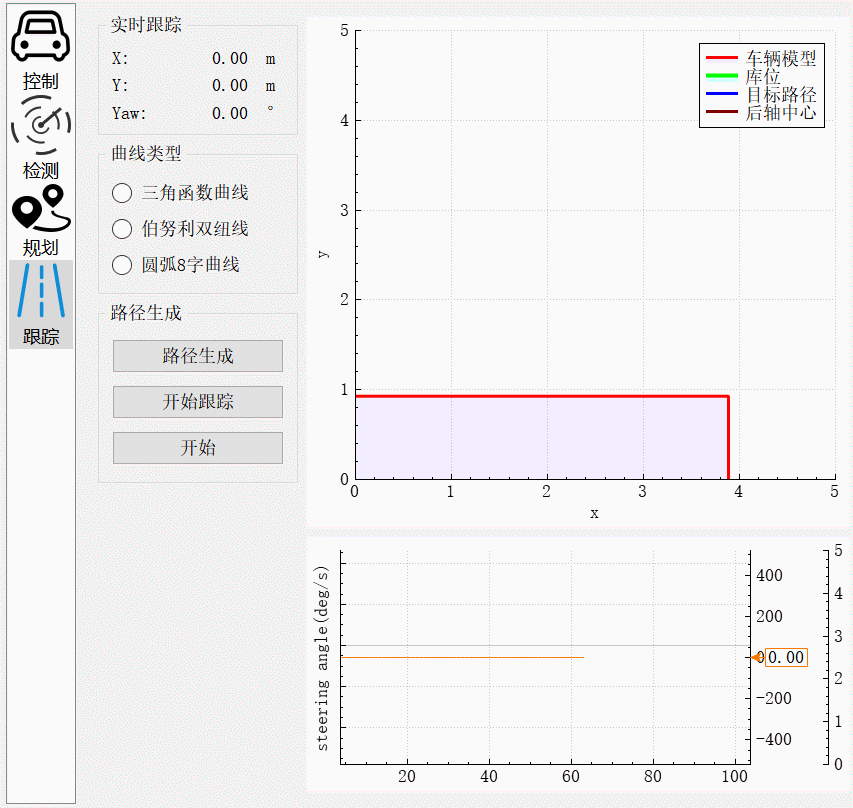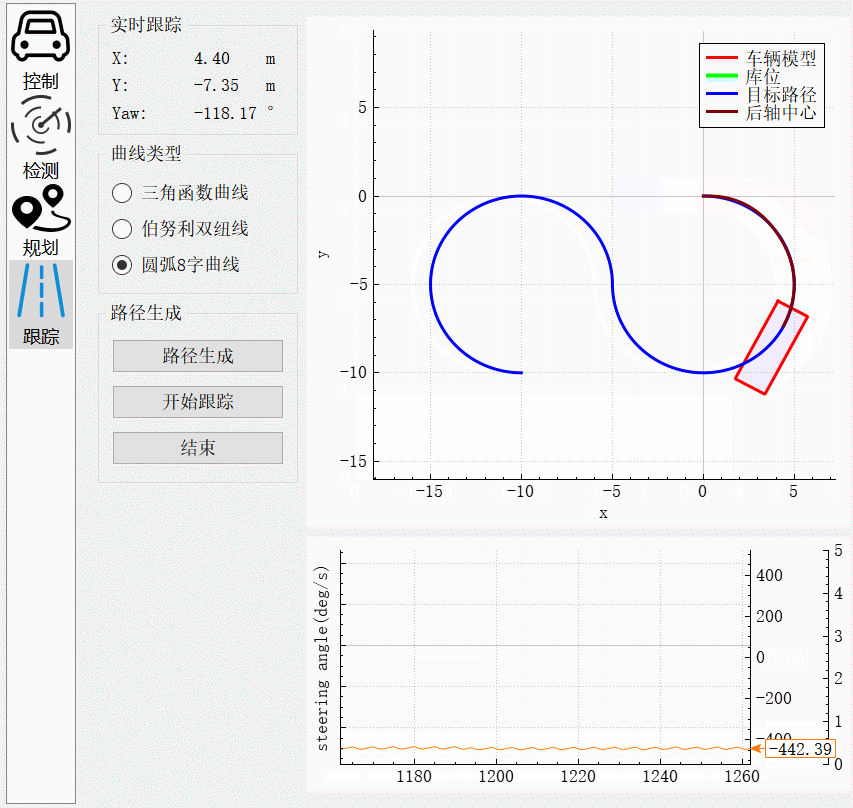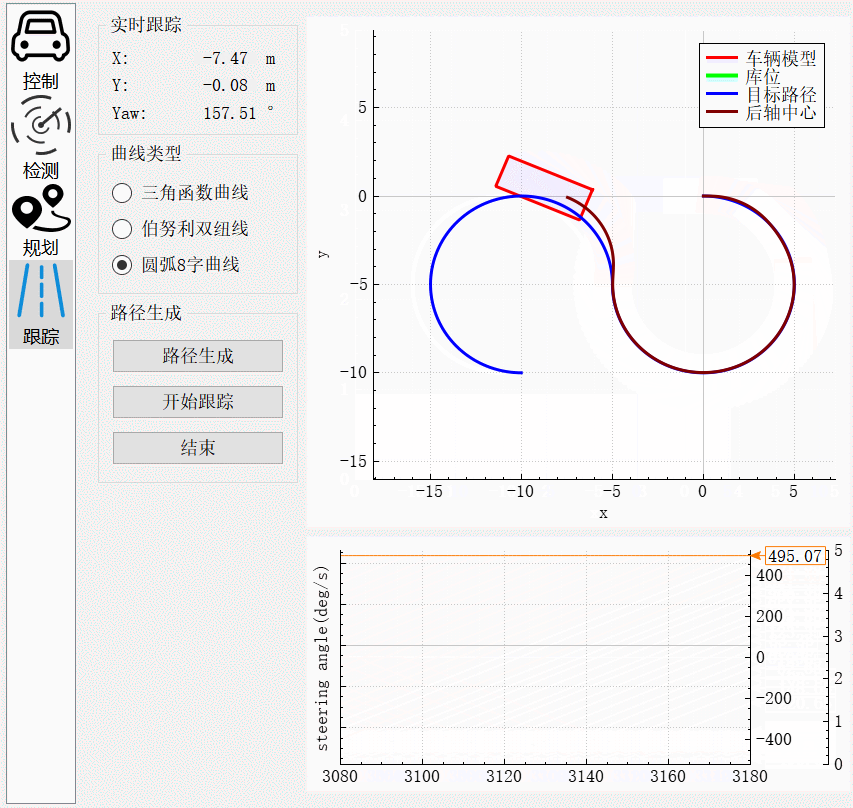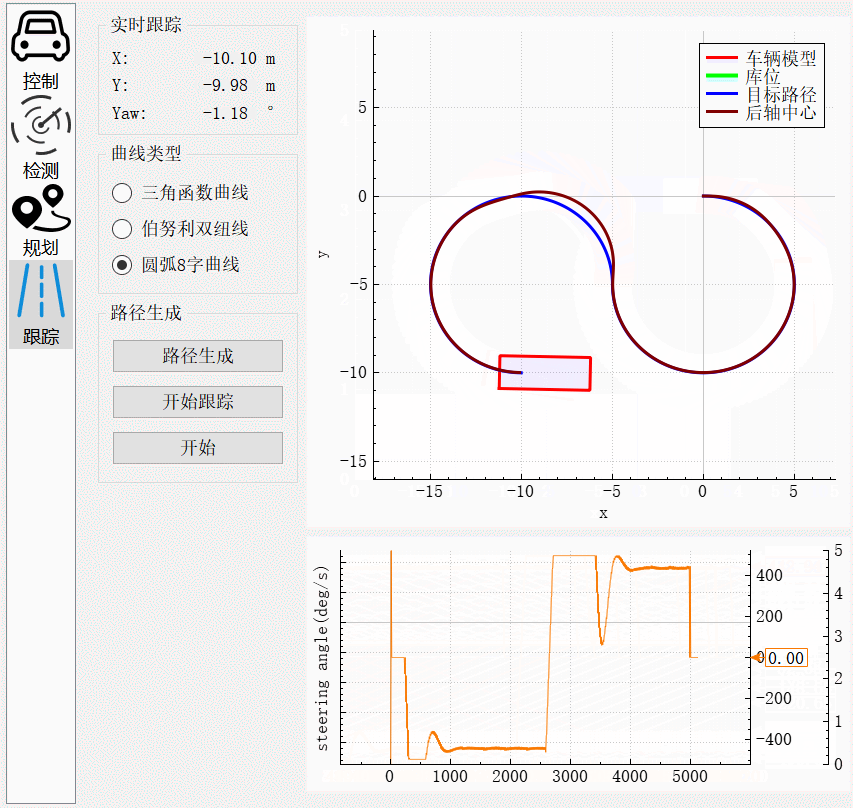
圆弧后退