控制算法-纯追踪法

概述

在机器人领域，一种最受欢迎的路径追踪算法就是几何路径追踪。这些方法主要利用车辆和路径之间的几何关系去设计相应的控制率解决路径跟踪问题。

几何车辆模型

对于几何路径跟踪一般简化车辆模型为单车模型，如上图所示，前轮转向角和后轴跟随曲线之间的几何关系可以表示如下：

\[ \tan(\delta) = \frac{L}{R}\tag{1} \]

其中，\(\delta\)代表前轮转向角、\(L\)代表车辆轴距、\(R\)代表转弯半径。

纯追踪

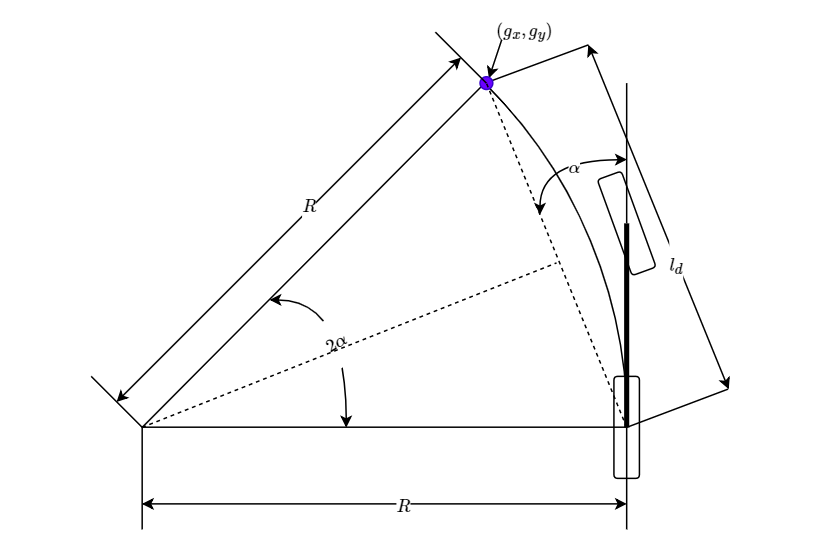
纯追踪算法包括几何关系计算出后轴位置与车辆前方目标曲线上目标点之间圆弧的曲率，其中目标点由从当前车辆后轴位置到目标路径的超前距离\(l_d\)决定。而车辆的转向角\(\delta\)只能使用目标点位置和车辆航向量与超前向量之间的夹角\(\alpha\)。由正弦定理得

\[ \frac{l_d}{\sin(2\alpha)} = \frac{R}{\sin(\frac{\pi}{2}-\alpha)}\tag{2} \]

根据三角函数性质，对等式(2)化简得

\[ \frac{l_d}{2\sin(\alpha)\cos(\alpha)} = \frac{R}{\cos(\alpha)} \tag{3} \]

由于\(\cos(\alpha) \neq 0\)，对等式(3)进一步化简得

\[ R = \frac{l_d}{2\sin(\alpha)} \tag{4} \]

故曲率表示为

\[ k = \frac{2\sin(\alpha)}{l_d} \tag{5} \]

根据等式(1)所示的车辆几何关系得

\[ \delta = \arctan(k\cdot L) \tag{6} \]

将等式(5)带入等式(6)得

\[ \delta = \arctan(\frac{2\sin(\alpha)L}{l_d})\tag{7} \]