控制算法-基于运动模型的LQR优化
概述
本文主要讲述基于运动学模型的车辆路径跟踪,并使用LQR算法求取最优控制率。

分析
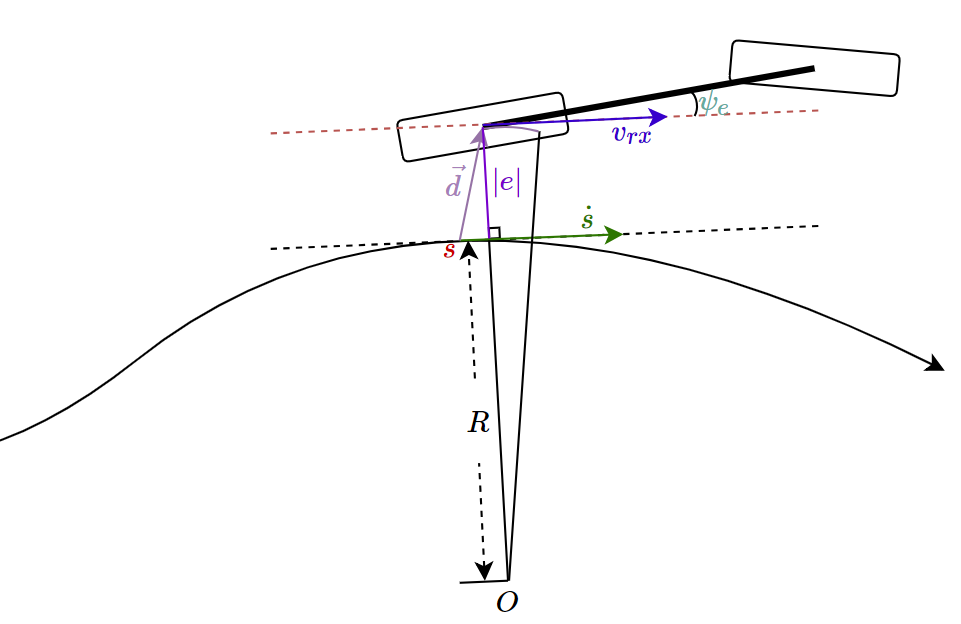
运动学微分方程
根据上图运动学特性易得
\[ \begin{array}{cl} \dot{s} &= \dfrac{v_{r}\cdot\cos(\psi_e)}{1-k(s)e}\\ \dot{e} &= v_r \cdot \sin(\psi_e)\\ \dot{\psi_e} &=\dfrac{v_r}{L}\tan(\delta) - \dfrac{v_{r}\cdot\cos(\psi_e)\cdot k(s)}{1-k(s)e} \end{array}\tag{1} \]
其中关于误差的微分方程如下:
\[ \begin{array}{cl} \dot{e}_s &= v_r \cdot \sin(e_\psi)\\ \dot{e}_\psi &= \dfrac{v_r}{L}\tan(\delta) - \dfrac{v_{r}\cdot\cos(e_\psi)\cdot k(s)}{1-k(s)e_s} \end{array}\tag{2} \]
线性化
将上述等式(2)中的\(\sin\)和\(\cos\)函数在\(e_\psi = 0\)处线性化,\(\tan\)函数在\(\delta = 0\)处线性化得
\[ \begin{array}{cl} \dot{e}_s &= v_r \cdot e_\psi \\ \dot{e}_\psi &= \dfrac{v_r}{L}\delta - \dfrac{v_{r}}{R-e_s} \end{array}\tag{3} \]
对等式(3)中\(e_s\)在\(e_s = 0\)处线性化得
\[ \begin{array}{cl} \dot{e}_s &= v_r \cdot e_\psi \\ \dot{e}_\psi &= \dfrac{v_r}{L}\delta - \dfrac{v_{r}}{R} - \dfrac{v_r}{R^2}e_s \end{array}\tag{4} \]
则相应的二阶导数为
\[ \begin{array}{cl} \ddot{e}_s &= \dot{v}_r \cdot e_\psi \\ \ddot{e}_\psi &= \dfrac{\dot{v}_r}{L}\delta - \dfrac{\dot{v}_{r}}{R} - \dfrac{\dot{v}_r}{R^2}e_s \end{array}\tag{5} \]
状态空间方程
整理等式(5),状态空间方程如下:
\[ \frac{\mathrm{d}}{\mathrm{d}t} \left[\begin{array}{cl} e_s\\ \dot{e}_s\\ e_{\psi}\\ \dot{e}_{\psi} \end{array}\right]= \left [ \begin{array}{cl} 0 & 1 & 0 & 0\\ 0 & 0 & \dot{v}_r & 0\\ 0 & 0 & 0 & 1\\ -\dot{v}_r \cdot k^2 & 0 & 0 & 0 \end{array} \right ] \left[ \begin{array}{cl} e_s\\ \dot{e}_s\\ e_{\psi}\\ \dot{e}_{\psi} \end{array} \right]+ \left[ \begin{array}{cl} 0\\ 0\\ 0\\ \dfrac{\dot{v}}{L} \end{array} \right]\delta \tag{6} \]
其中\(A=\left [ \begin{array}{cl} 0 & 1 & 0 & 0\\ 0 & 0 & \dot{v}_r & 0\\ 0 & 0 & 0 & 1\\ -\dot{v}_r \cdot k^2 & 0 & 0 & 0 \end{array}\right ]\),\(B=\left[ \begin{array}{cl} 0\\ 0\\ 0\\ \dfrac{\dot{v}}{L} \end{array}\right]\),\(X= \left[ \begin{array}{cl} e_s\\ \dot{e}_s\\ e_{\psi}\\ \dot{e}_{\psi} \end{array} \right]\),\(U=\delta\),等式(6)简写如下:
\[ \dot{X} = AX + BU \tag{7} \]
离散化
对上述(7)的连续状态空间方程离散化处理,得到如下离散化状态空间方程形式:
\[ X[k+1]=GX[k] + HU[k] \tag{8} \]
其中,\(G = I + AT\)、\(H = BT\),采用常规离散化方法得
\[ X[k+1] = (I + AT)X[k] + BTU[k] \tag{9} \]
其中\(A\)矩阵离散化得
\[ \begin{array}{cl} G &= I + AT\\ &=\left[ \begin{array}{cl} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right]+ \left [ \begin{array}{cl} 0 & 1 & 0 & 0\\ 0 & 0 & \dot{v}_{r(k)} & 0\\ 0 & 0 & 0 & 1\\ -\dot{v}_r k^2 & 0 & 0 & 0 \end{array} \right ] T\\ &=\left[ \begin{array}{cl} 1 & T & 0 & 0\\ 0 & 1 & \dot{v}_rT & 0\\ 0 & 0 & 1 & T\\ -\dot{v}_{r(k)} k^2T & 0 & 0 & 1 \end{array}\right] \end{array} \tag{10} \]
其中\(B\)矩阵离散化得
\[ \begin{array}{cl} H &= BT\\ &=\left[ \begin{array}{cl} 0\\ 0\\ 0\\ \dfrac{\dot{v}_{r(k)}T}{L} \end{array}\right] \end{array} \tag{11} \]
整理离散空间方程得
\[ \left[\begin{array}{cl} e_{s(k+1)}\\ \dot{e}_{s(k+1)}\\ e_{\psi(k+1)}\\ \dot{e}_{\psi(k+1)} \end{array}\right]= \left [ \begin{array}{cl} 1 & T & 0 & 0\\ 0 & 1 & \dot{v}_{r(k)}T & 0\\ 0 & 0 & 1 & T\\ -\dot{v}_{r(k)} k^2T & 0 & 0 & 1 \end{array} \right ] \left[ \begin{array}{cl} e_{s(k)}\\ \dot{e}_{s(k)}\\ e_{\psi(k)}\\ \dot{e}_{\psi(k)} \end{array} \right]+ \left[ \begin{array}{cl} 0\\ 0\\ 0\\ \dfrac{\dot{v}_rT}{L} \end{array} \right]\delta \tag{12} \]
相关简化
对上述(12)离散空间方程整理得
\[ \begin{array}{cl} e_{s(k+1)} &= e_{s(k)} + \dot{e}_{s(k)}T\\ \dot{e}_{s(k+1)} &= \dot{e}_{s(k)} + \dot{v}_{r(k)} T e_{\psi(k)}\\ e_{\psi(k+1)}&=e_{\psi(k)} + \dot{e}_{\psi(k)}T\\ \dot{e}_{\psi(k+1)} &= \dot{e}_{\psi(k)} + \dot{v}_{r(k)}T(\dfrac{\delta}{L} -k^2e_{s(k)}) \end{array} \tag{13} \]
等式(13)中\(\dot{e}_{s(k+1)}\)项结合等式(4)可进一步化简得
\[ \begin{array}{cl} \dot{e}_{s(k)} + \dot{v}_{r(k)} T e_{\psi(k)} &= v_{r(k)}e_{\psi(k)} + dv_{r(k)}e_{\psi(k)}\\ &= (v_{r(k)} + dv_{r(k)})e_{\psi(k)}\\ &=v_{r(k+1)}e_{\psi(k)} \end{array} \tag{14} \]
等式(13)中\(\dot{e}_{\psi(k+1)}\)项结合等式(4)可进一步化简得
\[ \begin{array}{cl} \dot{e}_{\psi(k)} + \dot{v}_{r(k)}T(\dfrac{\delta}{L} -k^2e_{s(k)}) &=v_{r(k)}(\dfrac{\delta}{L} - k^2e_{s(k)}) + dv_{r(k)}(\dfrac{\delta}{L} - k^2e_{s(k)})\\ &=(v_{r(k)} + dv_{r(k)})(\dfrac{\delta}{L}-k^2e_{s(k)})\\ &=v_{r(k+1)}(\dfrac{\delta}{L}-k^2e_{s(k)}) \end{array}\tag{15} \]
其中\(\dot{v}_r = \dfrac{dv_r}{dt}\),等式(13)结合等式(14)和(15)得
\[ \begin{array}{cl} e_{s(k+1)} &= e_{s(k)} + \dot{e}_{s(k)}T\\ \dot{e}_{s(k+1)} &= v_{r(k+1)} e_{\psi(k)}\\ e_{\psi(k+1)}&=e_{\psi(k)} + \dot{e}_{\psi(k)}T\\ \dot{e}_{\psi(k+1)} &= - v_{r(k+1)}k^2e_{s(k)} + \dfrac{v_{r(k+1)}}{L}\delta \end{array}\tag{16} \]
上述等式(16)整理为状态空间方程的形式为
\[ \left[\begin{array}{cl} e_{s(k+1)}\\ \dot{e}_{s(k+1)}\\ e_{\psi(k+1)}\\ \dot{e}_{\psi(k+1)} \end{array}\right]= \left [ \begin{array}{cl} 1 & T & 0 & 0\\ 0 & 0 & v_{r(k+1)} & 0\\ 0 & 0 & 1 & T\\ -v_{r(k+1)} k^2 & 0 & 0 & 0 \end{array} \right ] \left[ \begin{array}{cl} e_{s(k)}\\ \dot{e}_{s(k)}\\ e_{\psi(k)}\\ \dot{e}_{\psi(k)} \end{array} \right]+ \left[ \begin{array}{cl} 0\\ 0\\ 0\\ \dfrac{v_{r(k+1)}}{L} \end{array} \right]\delta \tag{17} \]
求解
采用LQR算法进行控制率求解。
- 确定迭代范围\(N\)
- 设置迭代初始值\(P_N=Q_f\)
- 循环迭代,\(t = N,\dots,1\)
\[ P_{t-1} = Q + A^TP_{t+1}A - A^TP_{t+1}B(R + B^TP_{t+1}B)^{-1}B^TP_{t+1}A \]
- 则反馈系数\(K_t = -(R + B^TP_{t+1}B)^{-1}B^TP_{t+1}A\),对于时间\(t=0,\dots,N-1\)
- 优化的控制量\(u_t^{lqr}=K_tx_t\)
参考
- LQR-离散时间有限边界