控制算法-滑模控制抖振消除
概述
在实际控制系统中,包括直流电机和飞机控制,通过连续或者平滑控制信号来避免控制抖振都是非常重要的方式。进一步说,飞机的气动表面不能高频来回运动,但同时对于边界模型不确定且存在外部干扰的控制系统,渴望保持其鲁棒性或不敏感度。

消抖方法
抖振消除
一个显而易见使控制函数连续且平滑的解决方案就是通过一些连续或平滑函数代替非连续函数\(v(\sigma) = -\rho sign(\sigma)\)。进一步说,它可以被"sigmoid function"替代。
\[ sign(\sigma) \approx \frac{\sigma}{\rvert \sigma \rvert + \varepsilon} \tag{1} \]
其中,\(\varepsilon\)是一个很小的正标量。可以看出,对于所有\(\sigma \neq 0\),下述等式成立:
\[ \lim_{\varepsilon \to 0}\frac{\sigma}{\rvert \sigma \rvert + \varepsilon} = sign(\sigma) \tag{2} \]
对于\(\varepsilon\)的选择需要权衡既要保持系统的性能理想又要确保控制的平滑。
关于 Sigmoid Function 的图形如下:
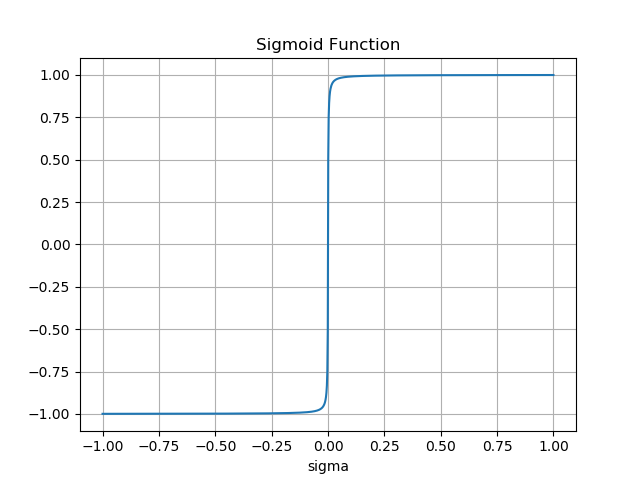
使用伪滑动模态控制率如下:
\[ u = -c \cdot x_2 - \rho\frac{\sigma}{\rvert \sigma \rvert + \varepsilon} \tag{3} \]
仿真结果
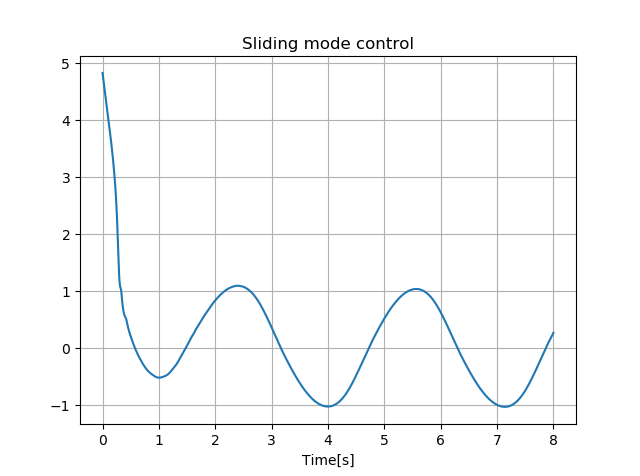
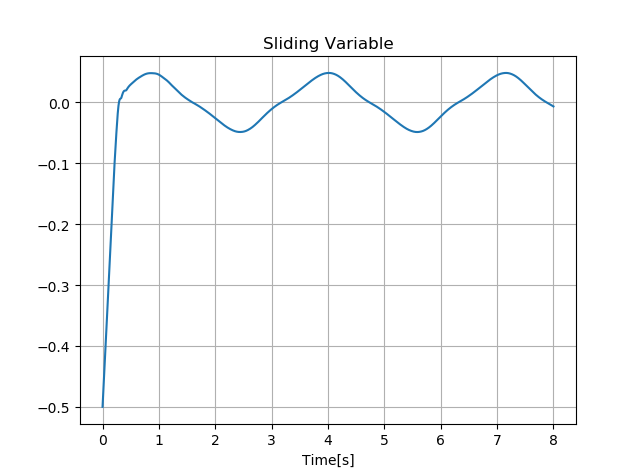
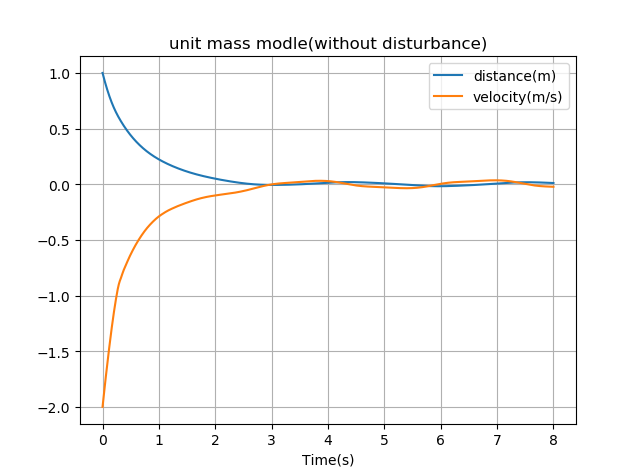
由上图可知,平滑控制函数不能够在存在外部干扰项\(f(x_1,x_2,t)\)时,使得滑模变量在有限时间内收敛于0。并且滑模变量和状态变量都不能收敛于0,但由于干扰项\(f(x_1,x_2,t) = \sin(2t)\)影响,使其收敛到原点附近的范围。实现平滑控制函数的代价是鲁棒性的损失和准确性降低。因为滑模变量在有限的时间内没有趋向于0,所以等式(3)所设计的平滑控制从技术上讲不是滑模控制,在系统中也不是理想的滑动模态。但是在等式(3)中平滑控制率下的系统性能接近于离散滑模控制下的系统性能。这就为我们将等式(3)对应的平滑控制率称为准滑模控制(quasi-sliding mode control)提供了依据,而当滑模面收敛于原点时,就叫做 准滑动模态(quasi-sliding mode)
抖振衰减
考虑设计另一种对边界干扰具有鲁棒性的连续控制器,设计思想就是根据控制函数的微分形式设计滑模控制器。在这种情况下,高频切换函数的积分作为实际控制是连续的。这种方法叫做 抖振衰减(chattering attenuation),这是因为在高频切换函数积分后仍然能在滑模控制中观察到一些周期性残差。
微分方程
系统微分方程如下:
\[ \left \{ \begin{array}{rl} &\dot{x}_1 = x_2 &x_1(0) &= x_{10}\\ &\dot{x}_2 = u + f(x_1,x_2,t) &x_2(0) &= x_{20}\\ &\dot{u} = v &u(0) &= 0 \end{array} \right. \tag{4} \]
如果滑模变量 \(\sigma = x_2 + c \cdot x_1\)被限制在有限时间\(t = t_r\)内收敛于0,同样对于所有\(t \geq t_r\),状态变量渐进收敛于0。这里假设\(\rvert f(x_1,x_2,t) \leq L\),此外其有界导数\(\rvert \dot{f}(x_1,x_2,t) \rvert \leq \bar{L}\)是平滑的。
辅助滑动变量
为了达到抖振衰减,定义如下辅助滑动变量
\[ s = \dot{\sigma} + \bar{c}\sigma \tag{5} \]
如果设计一个控制率\(v\)使得在有限时间内收敛\(s \to 0\),那么理想的滑动模态发生在如下滑模面上:
\[ s = \dot{\sigma} + \bar{c}\sigma = 0 \tag{6} \]
随着时间的递增,即使存在有界的干扰\(f(x_1,x_2,t)\),只要\(\sigma,\dot{\sigma} \to 0\),与此同时\(x_1,x_2 \to 0\)。但是因为原始滑模变量\(\sigma\)只是渐进收敛于0,所以对于系统(4)而言,这不是理想的滑动模态,而是 渐进滑动模态(asymptotic sliding mode),这就是衰减抖振所付出的代价。
根据等式(4)对辅组滑动变量\(s\)拆解得
\[ \begin{array}{rl} s &= \dot{\sigma} + \bar{c}\sigma\\ &= \dot{x}_2 + c\dot{x}_1 + \bar{c}(x_2 + cx_1)\\ &= u + f(x_1,x_2,t) + cx_2 + \bar{c}x_2 + c\bar{c}x_1\\ &=u + (c + \bar{c})x_2 + c\bar{c}x_1 + f(x_1,x_2,t) \end{array} \tag{7} \]
辅组滑动变量\(s\)求导得
\[ \begin{array}{rl} \dot{s} &= \dot{u} + (c + \bar{c})\dot{x}_2 + c\bar{c}\dot{x}_1 + \dot{f}(x_1,x_2,t)\\ &= v + (c + \bar{c})(u + f(x_1,x_2,t)) + c\bar{c}x_2 + \dot{f}(x_1,x_2,t)\\ &= v + (c + \bar{c})u + c\bar{c}x_2 + (c + \bar{c})f(x_1,x_2,t) + \dot{f}(x_1,x_2,t) \end{array} \tag{8} \]
根据李亚普洛夫稳定条件,设计滑模控制项\(v\),得到如下等式:
\[ s\dot{s} = s \bigl( v + (c + \bar{c})u + c\bar{c}x_2 + (c + \bar{c})f(x_1,x_2,t) + \dot{f}(x_1,x_2,t) \bigr) \tag{9} \]
选择如下控制率:
\[ v = -c\bar{c}x_2 - (c + \bar{c})u + v_1 \tag{10} \]
将等式(10)带入等式(9)得
\[ s\dot{s} = s \bigl( v_1 + (c + \bar{c})f(x_1,x_2,t) + \dot{f}(x_1,x_2,t) \bigr) \tag{11} \]
由于有界干扰项\(\rvert f(x_1,x_2,t) \leq L\)且\(\rvert \dot{f(x_1,x_2,t)} \rvert \leq \bar{L}\),故得
\[ s\dot{s} \leq sv_1 + \rvert s \rvert \bigl( (c + \bar{c})L + \bar{L}\bigr) \tag{12} \]
选择切换函数为\(v_1 = - \rho sign(s)\),其中\(\rho > 0\),带入等式(12)得
\[ s\dot{s} \leq \rvert s \rvert \bigl(-\rho + \bar{L} + (c + \bar{c})L \bigr) \tag{13} \]
根据有限时间收敛条件
\[ s\dot{s} \leq -\frac{\alpha}{\sqrt{2}}\rvert s\rvert \tag{14} \]
结合等式(13)和(14),计算控制增益\(\rho\)如下:
\[ \rho = \bar{L} + (c + \bar{c})L + \frac{\alpha}{\sqrt{2}} \tag{15} \]
驱使\(s\)在有限时间\(t_r \leq \frac{\sqrt{2}\rvert s(0) \rvert}{\alpha}\)内使\(s\)收敛于0的控制率\(v\)为
\[ v = -c\bar{c}x_2 - (c + \bar{c})u - \rho \cdot sign(s) \tag{16} \]
仿真结果
如下图所示,包含高频切换项的\(\rho sign(s)\)的控制率导致了抖振。
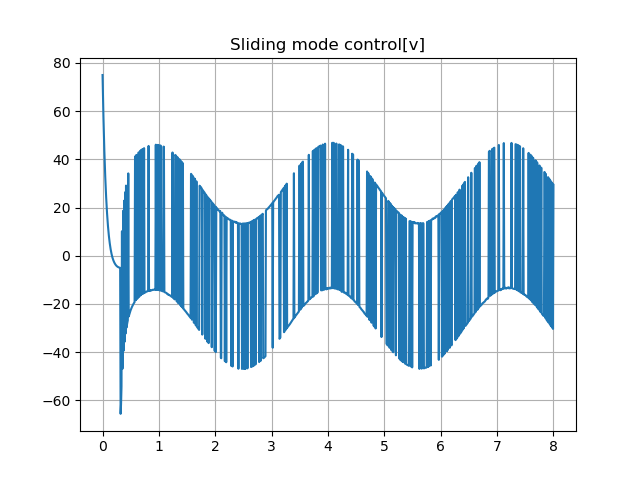
但如下图所示,抖振在实际物理控制率\(u = \int vdt\)中逐步衰减。
