控制算法-非时间参考的车辆路径跟踪
概述
基于非时间的参考的路径跟踪方法最早应用于机器人的路径跟踪系统,通过引入非时间参考量代替时间参考量,解决传统路径跟踪方法中将期望轨迹视为时间函数的问题。该方法选择移动机器人实际路径在某参考系下的x 轴投影作为非时间参考量。

非时间参考量下的微分方程
定义
定义一个非时间参考的标量\(s\),该\(s\)为时间t的单调递增函数。
\[ \left\{ \begin{array}{rl} &s = S(t)\\ &\dot{S}(t) > 0 \end{array} \right.\tag{1} \]
在车辆控制中,可以定义车辆的位移\(x\)为非时间参考量,为了满足随时间递增的要求,且泊车时速度为负值\((v<0)\),选取的非时间参考量为
\[ f = -x(t) \tag{2} \]
对上式求导得
\[ \dot{f}(t) = -v(t)\cos\psi(t) \tag{3} \]
由于车辆泊车过程中偏航角\(\psi \in (-\frac{\pi}{2},\frac{\pi}{2})\),故\(\dot{f}(t)>0\),满足非时间参考量随时间变化单调递增得要求。
基于非时间参考的车辆运动学方程可表示为: \[ \left \{ \begin{array}{cl} &\dfrac{dx}{df}= \dfrac{dx}{dt}\dfrac{dt}{df} = \dfrac{\dot{x}(t)}{\dot{f}(t)}\\ &\dfrac{dy}{df}= \dfrac{dy}{dt}\dfrac{dt}{df} = \dfrac{\dot{y}(t)}{\dot{f}(t)}\\ &\dfrac{d\psi}{df}= \dfrac{d\psi}{dt}\dfrac{dt}{df} = \dfrac{\dot{\psi}(t)}{\dot{f}(t)} \end{array} \right. \tag{4} \]
目标路径曲线
假设目标路径曲线函数为\(y_r = F(x_r)\),如果车辆可以无误差地跟踪,当车辆后轴中心横坐标为\(x_r\)时,对应的纵坐标为\(y_r\)、航向角为\(\psi_r\)、前轮等效转角为\(\delta_r\)。
- 目标航向角\(\psi_r\)计算
目标航向角\(\psi_r\)可以看作是函数\(y_r = F(x_r)\)在点\(x_r\)处的斜率所对应的航向角度,即
\[ \tan(\psi_r) = \dot{F}(x_r)= \frac{dy_r}{dx_r} \tag{5} \]
通过反三角函数求得目标航向角为
\[ \psi_r = \arctan\bigl(\dot{F}(x_r)\bigr)= \arctan(\frac{dy_r}{dx_r}) \tag{6} \]
- 目标转向角\(\delta_r\)计算
根据转向角的几何关系得
\[ \delta_r = \arctan(l*k) \tag{7} \]
其中,\(l\)代表车辆轴距、\(k\)代表点\(x_r\)处的目标路径曲线的曲率。
根据轨迹函数\(y_r = F(x_r)\)的一阶导数和二阶导数,曲率计算公式表示如下:
\[ k = \frac{\rvert\ddot{F}(x_r)\rvert}{[1+\dot{F}(x_r)^{2}]^\frac{3}{2}} \tag{8} \]
根据目标路径曲线,如果某段曲线是凸的,对应的二阶导数\(\ddot{F}(x_r) < 0\)。很明显,当偏航角满足\(\psi \in (-\frac{\pi}{2},\frac{\pi}{2})\)时,如果希望车辆跟踪凸形路线,对应的转向角应该为负值。同理,当曲线某段是凹形,对应的二阶导数\(\ddot{F}(x_r) > 0\),要想继续跟踪路线,转向角应该为正值。考虑\(\delta_r\)的正负性与曲线函数\(\ddot{F}(x_r)\)的二阶导数符号一致,等式(8)的绝对值符号可以消除,将其带入等式(7)得
\[ \delta_r = \arctan\Biggl( l*\frac{\ddot{F}(x_r)}{[1+\dot{F}(x_r)^{2}]^\frac{3}{2}}\Biggr)\tag{9} \]
将等式(5)带入等式(9)得
\[ \delta_r = \arctan\Bigl(l*\cos(\psi_r)^{3}\ddot{F}(x_r)\Bigr) \tag{10} \]
通过等式(6)和(10)可知,已知目标路径函数的前提下,可以计算得到横坐标为\(x_r\)下的车辆理想状态参数。
\[ \left \{ \begin{array}{cl} &\psi_r = \arctan\bigl(\dot{F}(x_r)\bigr)\\ &\delta_r = \arctan\Bigl(l*\cos(\psi_r)^{3}\ddot{F}(x_r)\Bigr) \end{array} \right. \tag{11} \]
车辆跟踪误差模型
车辆的跟踪误差表示如下: \[ \left \{ \begin{array}{rl} &e_x= 0\\ &e_y = y_r - y\\ &e_\psi = \psi_r - \psi \end{array} \right.\tag{12} \]
其中,\(y\)和\(\psi\)为车辆后轴中心点横坐标为\(x_r\)时,对应的车辆实际状态参数。\(e_x\)、\(e_y\)和\(e_\psi\)分别表示纵向误差、横向误差和航向角误差。
则以非时间参考量\(f = -x(t)\)为参考的路径跟踪误差微分方程如下:
- 纵向距离误差的微分方程
\[ \begin{array}{rl} \dfrac{dy_e}{-dx} &= \dfrac{d(y_r-y)}{-dx}\\ &=\dfrac{-dy_r}{dx} + \dfrac{dy}{dx}\\ &=-tan(\psi_r) + \tan(\psi) \end{array}\tag{13} \]
- 偏航角误差微分方程
由等式(10)得
\[ \tan(\delta_r) = l*\cos(\varphi_r)^{3}\ddot{F}(x_r) \tag{14} \]
等式(5)对\(x\)求导得
\[ [1 + \tan(\psi_r)^2]*\frac{d\psi_r}{dx} = \ddot{F}(x_r) \tag{15} \]
等式(15)带入等式(14)得
\[ \begin{array}{cl} \tan(\delta_r) &= l*\cos(\psi_r)^{3}*[1+\tan(\psi_r)^{2}]*\dfrac{d\psi_r}{dx}\\ &= l*\cos(\psi_r)*\dfrac{d\psi_r}{dx} \end{array} \tag{16} \]
由于\(\psi \in (-\frac{\pi}{2},\frac{\pi}{2})\),故\(\cos(\psi_r) \neq 0\),等式(16)移项整理得
\[ \frac{d\psi_r}{dx} = \frac{\tan(\delta_r)}{l*\cos(\psi_r)} \tag{17} \]
根据等式(17),可得航向角误差的微分方程为
\[ \begin{array}{rl} \dfrac{d\psi_e}{-dx} &= -\dfrac{d\psi_r}{dx} + \dfrac{d\psi}{dx}\\ &=-\dfrac{\tan(\delta_r)}{l*\cos(\psi_r)} + \dfrac{\tan(\delta)}{l*\cos(\psi)} \end{array}\tag{18} \]
整理等式(13)和(18)得
\[ \left \{ \begin{array}{rl} & \dfrac{de_y}{-dx} = -tan(\psi_r) + \tan(\psi)\\ & \dfrac{de_\psi}{-dx} = -\dfrac{\tan(\delta_r)}{l*\cos(\psi_r)} + \dfrac{\tan(\delta)}{l*\cos(\psi)} \end{array} \right. \tag{19} \]
滑模控制器设计
滑模控制算法因算法简单、鲁棒性好、适应性强、实用性而被广泛运用。滑模控制的核心是设计处合适的切换函数和变结构控制率,使系统状态轨迹线能快速到达设计的切换面进行滑动模态运动。
微分方程
系统参考状态量为:
\[ \left \{ \begin{array}{rl} &x_1 = y_r - y\\ &x_2 = -tan(\psi_r) + \tan(\psi) \end{array} \right. \tag{20} \]
结合等式(12)、(17),对应的微分方程为:
\[ \left \{ \begin{array}{rl} &\dot{x_1} &= \dfrac{dx_1}{-dx} &= \dfrac{y_r - y}{-dx} &= x_2\\ &\dot{x_2} &= \dfrac{dx_2}{-dx} &=\dfrac{-tan(\psi_r) + \tan(\psi)}{-dx} &= \dfrac{\tan(\delta_r)}{l*\cos(\psi_r)^3} - \dfrac{\tan(\delta)}{l*\cos(\psi)^3} \end{array} \right. \tag{21} \]
滑模面
定义滑模变量\(s\)为:
\[ s = x_2 + c \cdot x_1 \tag{22} \]
其中\(c > 0\),结合等式(20)和(21),对等式(22)求导得:
\[ \dot{s}=\frac{ds}{-dx} = \dfrac{\tan(\delta_r)}{l*\cos(\psi_r)^3} -\dfrac{\tan(\delta)}{l*\cos(\psi)^3} + c \cdot \bigl(\tan(\psi)-tan(\psi_r)\bigr) \tag{23} \]
基于趋近律的滑模控制
采用指数趋近率\(\dot{s} = -\rho \cdot sign(s) - k\cdot s\),可以减弱变结构控制系统的抖振。通过调整趋近率参数\(\rho\)和\(k\),既可以保证滑动模态到达过程的动态品质,又可以减弱控制信号的高频抖振,但是较大的\(\rho\)会引起抖振。
采用指数趋近率为
\[ \dot{s} = -\rho \cdot sign(s) - k\cdot s \tag{24} \]
其中\(\rho > 0\)、\(k > 0\)、\(sign(s)\)为符号函数。
稳定判据
定义李亚普洛夫函数(Lyapunov)形式如下:
\[ V = \frac{1}{2}s^2 \tag{25} \]
为了使滑模变量在平衡点\(s = 0\)处渐进稳定,根据李亚普洛夫稳定判据,必须满足下面两个条件:
- \(\begin{array}{rl}\dot{V} < 0 &(s \neq 0)\end{array}\)
- \(\lim_{\rvert s\rvert \to \infty}V = \infty\)
由等式(25)的形式可知,条件2明显满足。将等式(24)所示的指数趋近率代入,并计算\(\dot{V}\)得
\[ \begin{array}{rl} \dot{V} = s\dot{s} &= s(-\rho \cdot sign(s) - k\cdot s)\\ &=-k \cdot s^2 - \rho \cdot sign(s) \cdot s\\ &= -k \cdot \rvert s \rvert ^2 - \rho \cdot \rvert s \rvert \end{array} \tag{26} \]
其中\(k > 0\),\(\rho > 0\),很明显等式(26)中\(\dot{V} < 0\),即满足条件1。因此采用等式(24)的指数趋近率可以使滑模变量渐进稳定。
控制率
驱使滑模变量\(s\)变为0的控制率可以根据等式(23)和(24)得:
\[ \dfrac{\tan(\delta_r)}{l*\cos(\psi_r)^3} -\dfrac{\tan(\delta)}{l*\cos(\psi)^3} + c \cdot \bigl(\tan(\psi)-tan(\psi_r)\bigr) = -\rho \cdot sign(s) - k\cdot s \tag{27} \]
根据等式(27),提取\(\delta\)项得
\[ \delta = \arctan \Biggl( l*\cos(\psi)^3 \cdot \Bigl( \dfrac{\tan(\delta_r)}{l*\cos(\psi_r)^3} + c \cdot \bigl(\tan(\psi)-tan(\psi_r)\bigr) + \rho \cdot sign(s) + k\cdot s \Bigr) \Biggr) \tag{28} \]
等式(28)进一步化简为如下形式:
\[ \delta = \arctan \Biggl( l*\cos(\psi)^3 \cdot \Bigl( \dfrac{\tan(\delta_r)}{l*\cos(\psi_r)^3} + c \cdot x_2 + \rho \cdot sign(s) + k\cdot s \Bigr) \Biggr) \tag{29} \]
切换函数
由于上述滑模控制器中使用的是符号函数\(sign(s)\),系统会出现不连续的开关特性,使得滑模变结构系统在滑动模态下存在高频的振动现象,从而导致路径跟踪过程中控制器出现较大波动,继而影响泊车的控制精度。
为了抑制振动,本文分别采用饱和函数\(sat(\dfrac{s}{\Delta})\)和\(sigmoid\)函数代替符号函数\(sign(s)\),保证系统的切换面附近光滑连续。
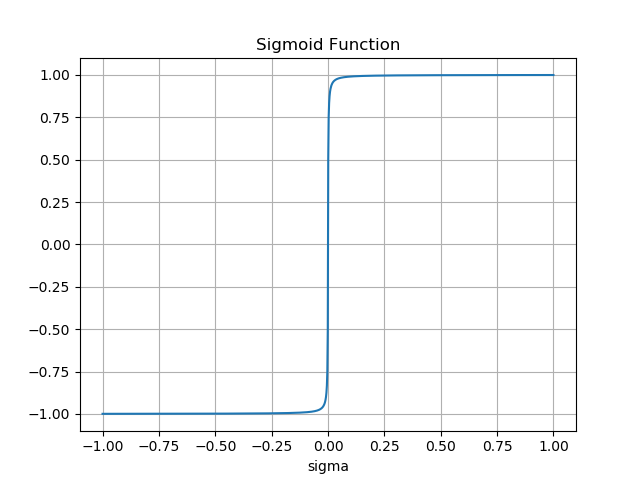
- Sigmoid Function: \[ Sigmoid(x) = \frac{x}{\rvert x \rvert + \varepsilon} \tag{30} \]
其中\(\varepsilon\)是很小的正标量,下图为\(\varepsilon = 0.001\)时,\(Sigmoid(x)\)函数的波形图入下:
- Sat Function:
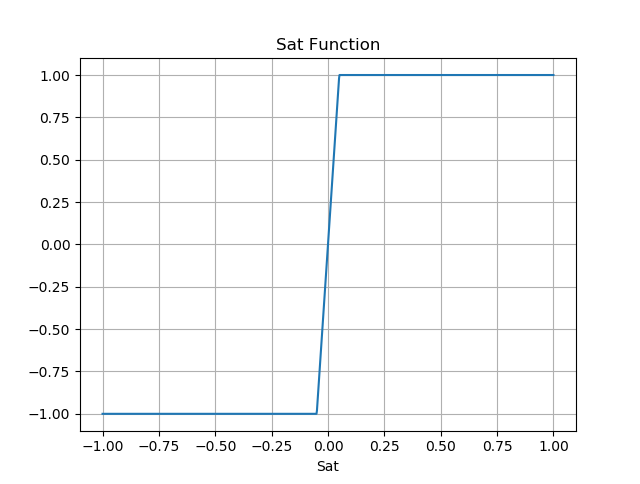
\[ Sat(\frac{x}{\Delta}) = \left \{ \begin{array}{rl} &1 & , &x \geq \Delta\\ &\dfrac{x}{\Delta} & , &\rvert x \rvert < \Delta\\ &-1 & , &x \leq -\Delta \end{array} \right. \tag{31} \]
其中,\(\Delta\)为很小的正标量,代表边界层的厚度,当\(\Delta = 0.05\)时,\(Sat(x)\)波形图如下:
性能分析
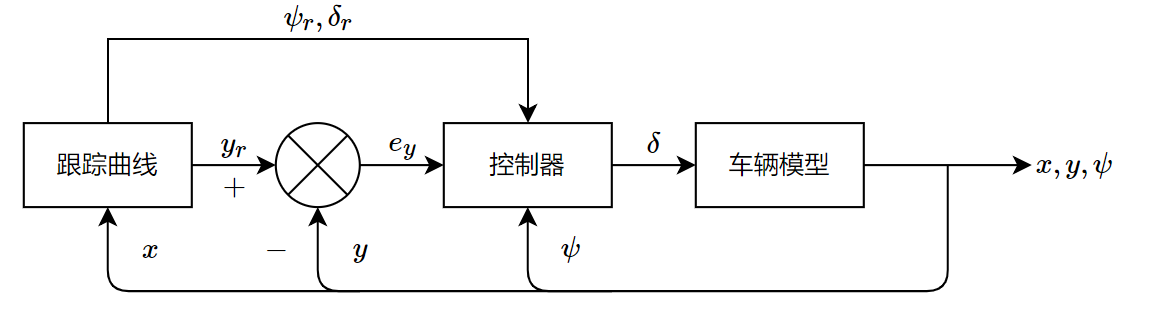
根据如下控制系统框图,搭建仿真环境。
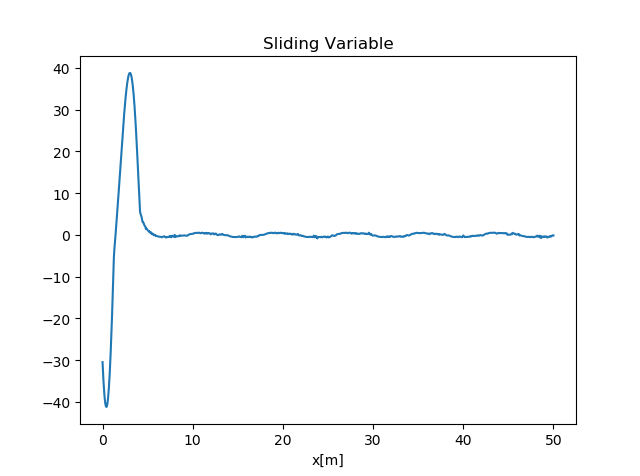
- 滑模变量\(s\) 下图所示,是滑模变量\(s\)随距离\(x\)变化的图形。随着距离的增大,滑模变量\(s\)趋近于0,系统也趋近于稳定,但是滑模变量在0附近存在抖振。
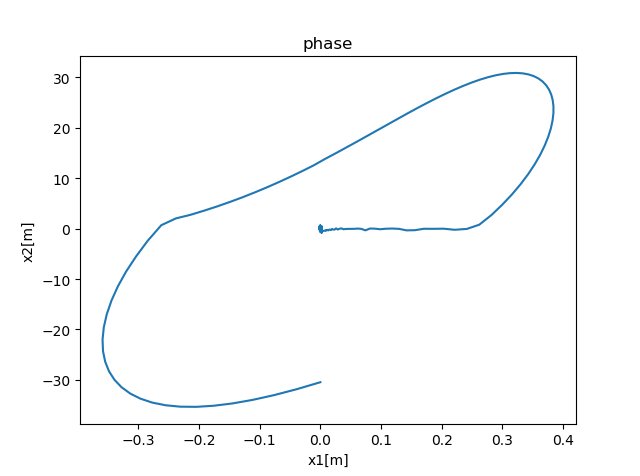
- 相图 如下图所示,是系统的相图,可以看出,系统逐渐收敛于原点。
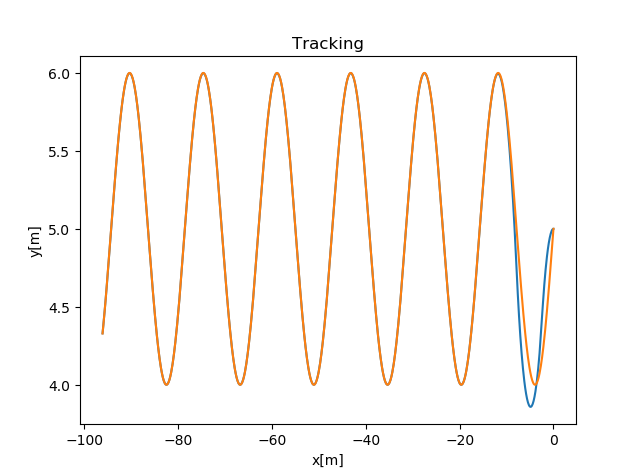
- 路径跟踪图 如下图所示,是系统的路径跟踪波形图。刚开始时,跟踪存在偏差。经过一段时间的修正,跟踪路径趋近于一致。
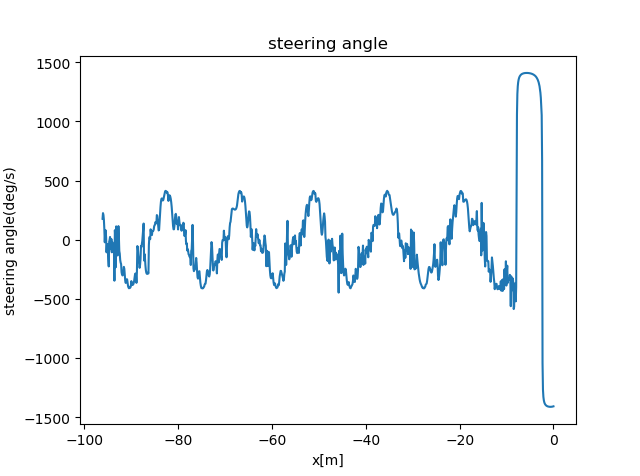
- 转向角图 如下图所示,是系统控制产生的转向角信号。从图中可以发现,系统在趋于稳定时,控制信号存在抖振现象。
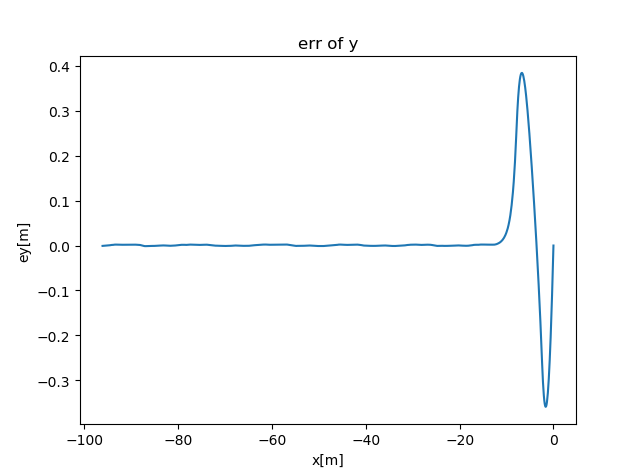
- 轨迹误差图 如下图所示,是系统产生的轨迹误差图,随着时间推移,估计误差趋近于0。