控制算法 - 滑模控制介绍

一维运动模型

考虑简单的单位质量块的一维运动模型，使用位移和速度状态变量进行描述。

定义位移变量 $x_1=x$ 和速度变量 $x_2=\dot{x_1}=v$，运动模型的微分形式使用 $x_1$、$x_2$ 表示如下：

$$\begin{array}{}\text{(1)}& \{\begin{array}{rll}& \dot{x_1}=x_2& x_1(0)=x_{10}\\ & \dot{x_2}=u+f(x_1,x_2,t)& x_2(0)=x_{20}\end{array}\end{array}$$

其中，$u$ 代表控制力，干扰项 $f(x_1,x_2,t)$ 包括干粘摩檫力的影响和一些未知的阻力，并假定有界。

$$\begin{array}{}\text{(2)}& |f(x_1,x_2,t)|⩽L>0\end{array}$$

问题关键在于设计一个反馈控制率 $u=u(x_1,x_2)$，驱动质量块渐进到达原点。换句话说，控制变量 $u=f(x_1,x_2)$ 应该驱使状态变量趋近于 0：$\underset{t\to \mathrm{\infty }}{lim}{x}_1,x_2=0$。

这个问题看似简单，但对于存在未知的边界干扰项 $f(x_1,x_2,t)$ 的情况下，使系统渐进收敛仍然存在着挑战。

状态反馈控制

例如，通过一个线性状态反馈控制率

$$\begin{array}{}\text{(3)}& \begin{array}{ccc}u=-k_1{x}_1-k_2{x}_2,& \text{其中}(k_1>0,& k_2>0)\end{array}\end{array}$$

在外界干扰项 $f(x_1,x_2,t)\equiv 0$，即不存在外界干扰时，系统可以实现渐进收敛。

仿真结果

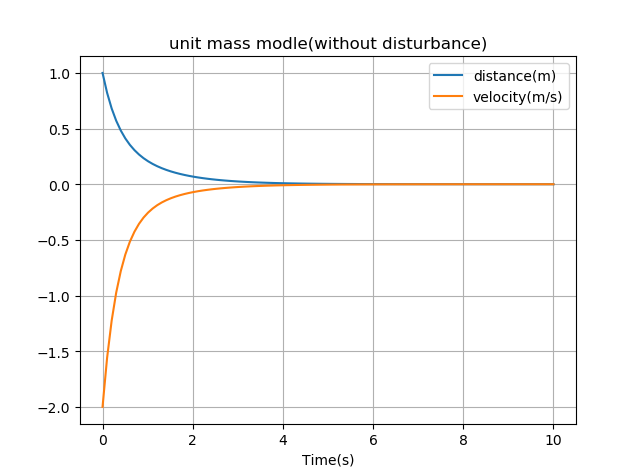
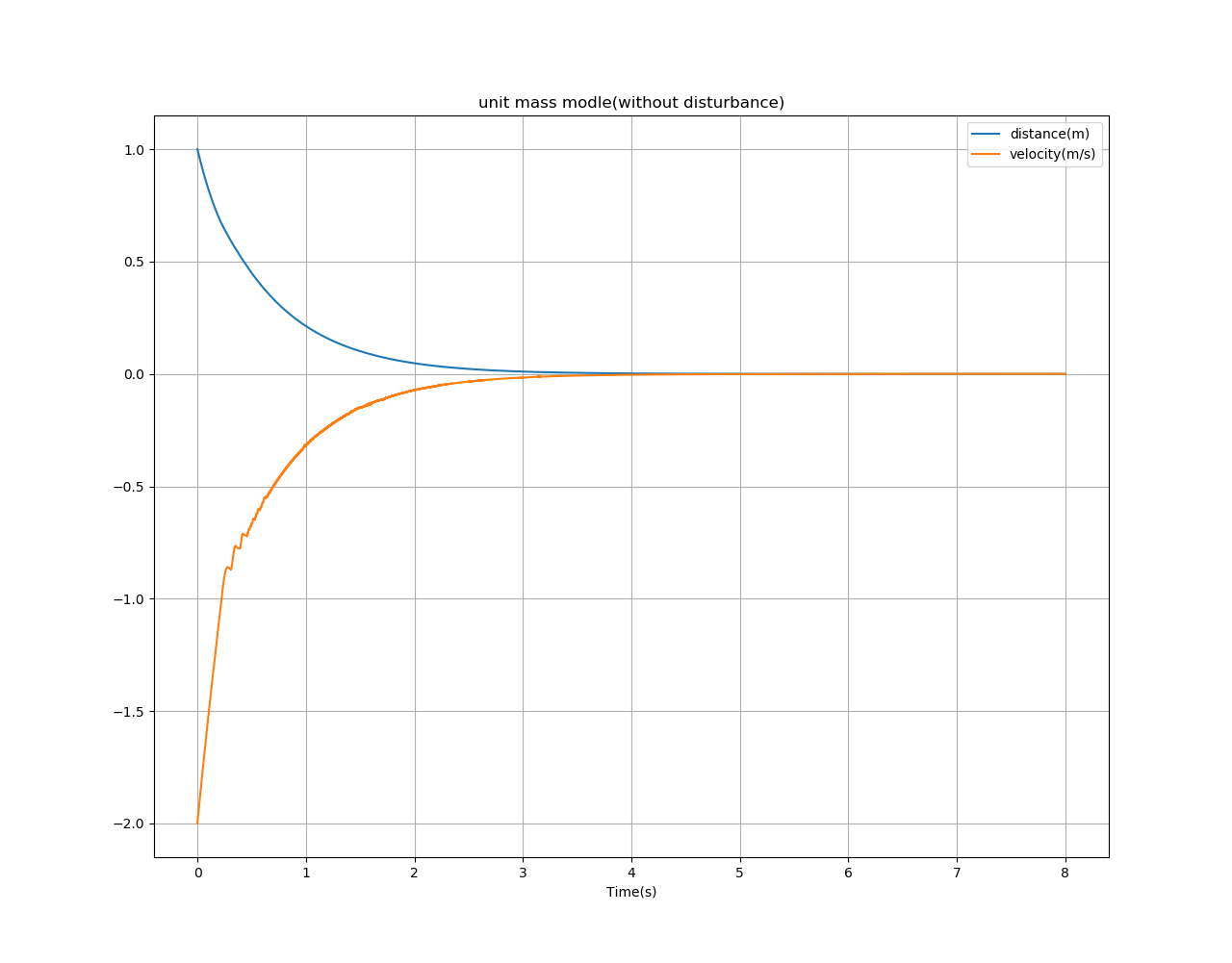
• 初始条件 $x_{10}=1$、$x_{20}=-2$、控制率参数 $k_1=3$、$k_2=4$。

如下图所示，是无外界干扰项时的渐近收敛效果图，图中蓝色线代表距离 $x$，橘黄色线代表速度 $v$，可以看出在反馈控制率 $u=u(x_1,x_2)$ 的作用下，距离和速度值都趋近于 0。

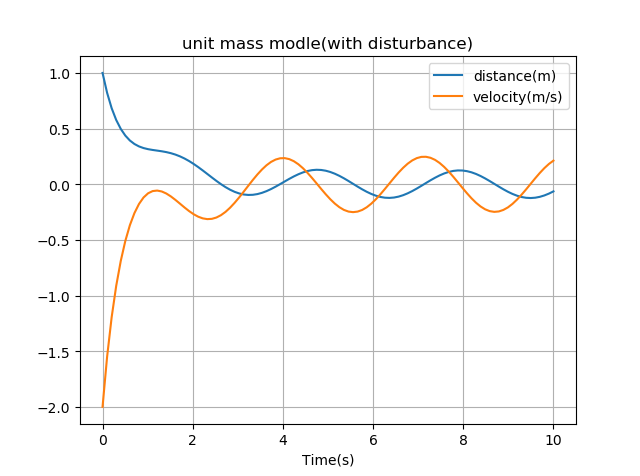
加入外部干扰 $f(x_1,x_2,t)=\sin (2t)$，响应波形如下：

对于干扰项 $|f(x_1,x_2,t)|\le L>0$, 产生的状态边界范围为 $\mathrm{\Omega }=(k_1,k_2,L)$ 。

现在问题在于，仅使用未知扰动范围的知识是否可以解决规定的控制问题。

滑模控制的主要特性

介绍对于等式 (1) 系统，所需的补偿动力。一个较好的替代这些动力学特性的是齐次线性时不变微分方程：

$$\begin{array}{}\text{(4)}& \begin{array}{rl}{\dot{x}}_1+c\cdot x_1=0,& c>0\end{array}\end{array}$$

因为 $x_2(t)={\dot{x}}_1(t)$, 等式 (4) 的通用解和它的微分形式如下：

$$\begin{array}{}\text{(5)}& \begin{array}{}& x_1(t)=x_1(0)\exp (-ct)\\ & x_2(t)=\dot{x_1}(t)=-c\cdot x_1(0)\exp (-ct)\end{array}\end{array}$$

从等式 (5) 可以看出，$x_1(t)$ 和 $x_2(t)$ 都是逐渐趋近于 0。注意，无干扰项 $f(x_1,x_2,t)$ 的状态补偿动力学是很明显的。如何获得这些补偿动力。

滑模变量

首先介绍一个等式 (1) 系统的状态空间的新变量 (滑模变量)：

$$\begin{array}{}\text{(6)}& \sigma =\sigma (x_1,x_2)=x_2+c\cdot x_1\end{array}$$

在给定等式 (5) 收敛率且存在有界干扰 $f(x_1,x_2,t)$ 的情况下，为了使状态变量 $x_1$，$x_2$ 逐渐收敛于 0，即 $\underset{t\to \mathrm{\infty }}{lim}{x}_1,x_2=0$，不得不通过控制率 $u$ 使得等式 (6) 的变量 $\sigma$ 在有限的时间内趋于 0。

为了完成这个任务利用李亚普洛夫函数技术，结合等式 (1) 和 (6) 推动出关于滑模变量 $\sigma$ 的动力学方程如下：

$$\begin{array}{}\text{(7)}& \begin{array}{rl}\dot{\sigma }=c\cdot x_2+f(x_1,x_2,t)+u,& \sigma (0)={\sigma }_0\end{array}\end{array}$$

稳定判据

李亚普洛夫函数 (Lyapunov) 形式如下：

$$\begin{array}{}\text{(8)}& V=\frac{1}{2}{\sigma }^2\end{array}$$

为了使等式 (6) 在平衡点 $\sigma =0$ 处渐进稳定，根据李亚普洛夫稳定判据，必须满足下面两个条件：

1. $\begin{array}{rl}\dot{V}<0& (\sigma \ne 0)\end{array}$
2. $\underset{|\sigma |\to \mathrm{\infty }}{lim}V=\mathrm{\infty }$

由等式 (8) 知，条件 2 明显满足。为了满足有限时间内渐进稳定，条件 (1) 可以修改为：

$$\begin{array}{}\text{(9)}& \dot{V}\le -\alpha V^{\frac{1}{2}},\alpha >0\end{array}$$

在时间间隔 $0\le \tau \le t$ 内，对等式 (9) 所示的微分方程进行变量分离求积分得

$$\begin{array}{}\text{(10)}& \begin{array}{rl}{\int }_0^{t}V(\tau {)}^{-\frac{1}{2}}dV(\tau )& \le -\alpha \ast {\int }_0^{t}1d\tau \\ 2\ast V(\tau {)}^{\frac{1}{2}}{|}_0^t& \le -\alpha \ast \tau {|}_0^t\\ 2\ast [V(t{)}^{\frac{1}{2}}-V(0{)}^{\frac{1}{2}}]& \le -\alpha \ast t\\ V(t{)}^{\frac{1}{2}}& \le -{\displaystyle \frac{1}{2}}\alpha \ast t+V(0{)}^{\frac{1}{2}}\end{array}\end{array}$$

故 $V(t)$ 在有限时间 $t_r$ 达到 0 时的边界，根据等式 (26) 得

$$\begin{array}{}\text{(11)}& t_r\le \frac{2V(0{)}^{\frac{1}{2}}}{\alpha }\end{array}$$

因此，设计一个控制器 $u$ 满足等式 (9)，使得变量 $s$ 在有限的时间内趋近于 0 并在之后一直保持。

$V$ 的微分计算如下：

$$\begin{array}{}\text{(12)}& \dot{V}=\sigma \dot{\sigma }=\sigma (c\cdot x_2+f(x_1,x_2,t)+u)\end{array}$$ 假设 $u=-c\cdot x_2+v$，并将其带入等式 (12) 得 $$\begin{array}{}\text{(13)}& \dot{V}=\sigma (f(x_1,x_2,t)+v)=\sigma \cdot f(x_1,x_2,t)+\sigma v\le |\sigma |L+\sigma v\end{array}$$

此处选择 $v=-\rho sign(\sigma )$，该函数表示为

$$\begin{array}{}\text{(14)}& sign(x)=\{\begin{array}{rll}& 1& x>0\\ & & & \\ & -1& x<0\end{array}\end{array}$$ 并且

$$\begin{array}{}\text{(15)}& sign(0)\in [-1,1]\end{array}$$

由于 $\rho >0$，将其带入等式 (13) 得

$$\begin{array}{}\text{(16)}& \dot{V}\le |\sigma |L-|\sigma |\rho =|\sigma |(L-\rho )\end{array}$$

考虑到等式 (8) 的形式，等式 (9) 可以表示为

$$\begin{array}{}\text{(17)}& \dot{V}\le -\alpha V^{\frac{1}{2}}=-\frac{\alpha }{\sqrt{2}}|\sigma |,\alpha >0\end{array}$$

结合等式 (16) 和等式 (17) 得

$$\begin{array}{}\text{(18)}& \dot{V}\le |\sigma |(L-\rho )=-\frac{\alpha }{\sqrt{2}}|\sigma |\end{array}$$

最终控制增益可以表示为

$$\begin{array}{}\text{(19)}& \rho =L+\frac{\alpha }{\sqrt{2}}\end{array}$$

所以最终使滑模变量 $\sigma$ 在有限时间内趋近于 0 的控制率 $u$ 为

$$\begin{array}{}\text{(20)}& u=-c\cdot x_2-\rho \cdot sign(\sigma )\end{array}$$

1. 显然，为了成功地设计出等式 (20) 中的控制器，$\dot{\sigma }$ 必须是控制率 $u$ 的函数。当设计像等式 (6) 中的滑模变量时，这个特性必须考虑其中。
2. 等式 (19) 中控制增益 $\rho$ 的第一项被设计用来补偿有界干扰项 $f(x_1,x_2,t)$，同时第二项 $\frac{\alpha }{\sqrt{2}}$ 负责确定滑模面的到达时间。$\alpha$ 的数值越大，到达时间就越短。

基本定义

• 滑模变量

等式 (6) 中定义的变量 $\sigma$ 叫做 滑模变量 (sliding variable)

• 滑模面

结合等式 (4) 和 (5)，可以重新写成如下形式： $$\begin{array}{}\text{(21)}& \sigma =x_2+c\cdot x_1=0,c>0\end{array}$$ 相当于在系统 (1) 状态空间内的一条直线，这条直线被称为 滑模面 (sliding surface)。

考虑到等式 (9) 可以等效于

$$\begin{array}{}\text{(22)}& \sigma \dot{\sigma }\le -\frac{\sigma }{\sqrt{2}}|\sigma |\end{array}$$

等式 (22) 经常被称为 到达条件 (reachability condition)。满足到达条件意味着等式 (1) 系统的轨迹趋向于滑模面，并在此后一直保持。

• 滑模控制

等式 (20) 所对应的控制率 $u=u(x_1,x_2)$ 驱使状态变量 $x_1$、$x_2$ 在有限时间 $t_r$ 内趋近于滑模面，并在存在有界干扰项 $f(x_1,x_2,t)$ 的情况下保持在该平面上，这个控制率 $u$ 就叫做 滑模控制。并且对于所有的 $t>t_r$，系统都将产生一个理想滑动模态。

仿真结果

初始条件为 $x_1(0)=1，x_2(0)=-2$，控制增益为 $\sigma =2$，滑模参数为 $c=1.5$ 同时干扰项为 $f(x_1,x_2,t)=\sin (2t)$。 使用等式 (20) 的滑模控制率的仿真结果如下：

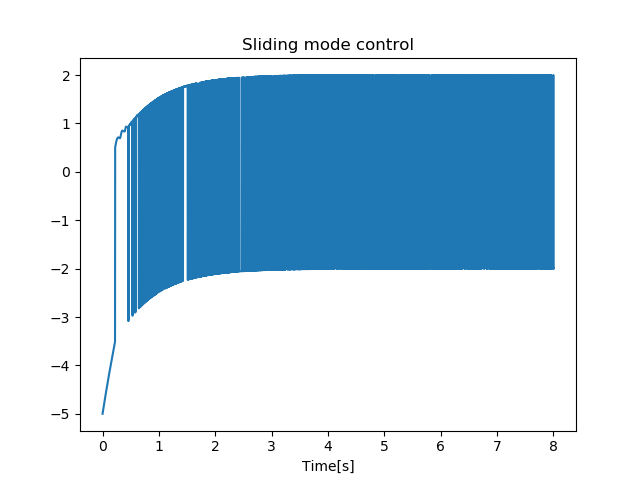
下图表明，在有限的时间内，滑模变量趋近于 0。

在干扰项作用的情况下，状态变量 $x$ 和 $v$ 逐渐收敛到 0。

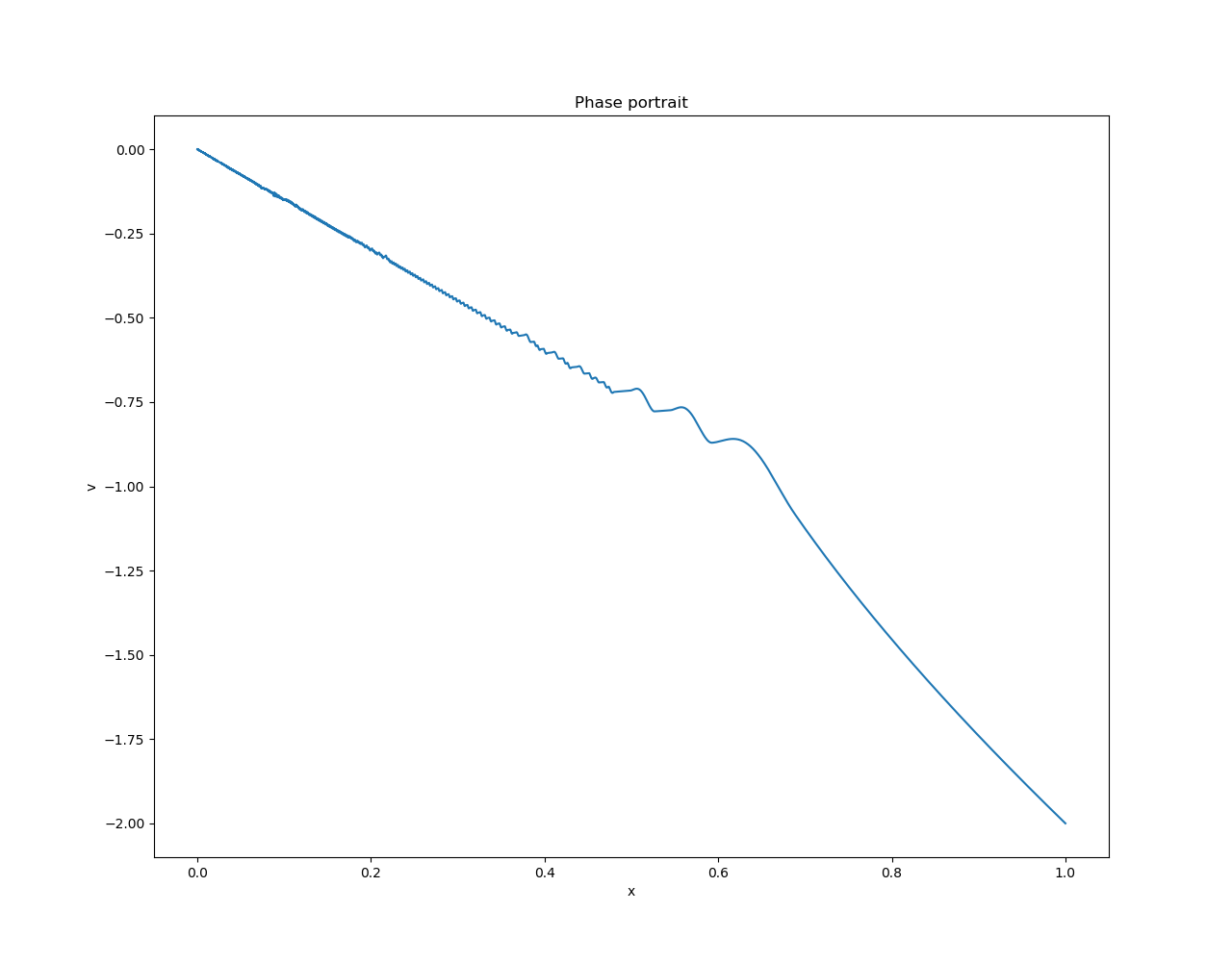
相图如下，展示了到达相位和滑移相位。

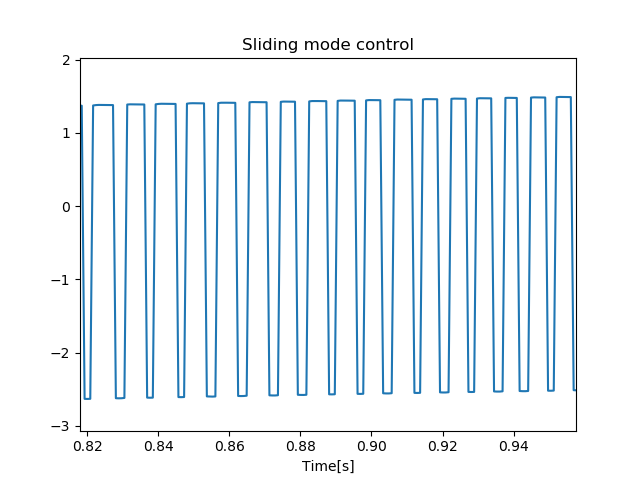
对上面的相图进行局部放大发现，在滑模状态下，状态变量存在小幅度且高频率的蜿蜒运动。

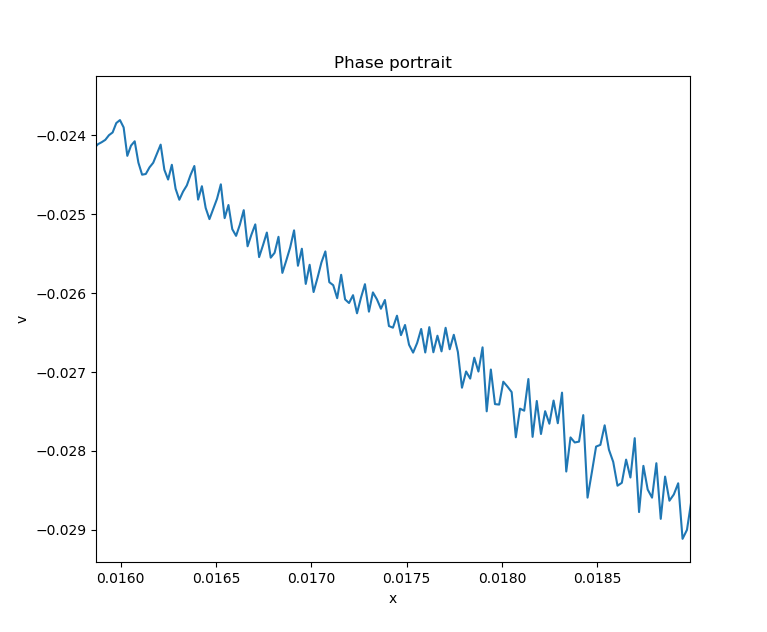
理想的滑模切换频率应该接近于无限并且蜿蜒运动的振幅接近于 0。从下图可知，符号函数 $sign$ 不完美表现为在滑动模态中产生了有限幅度和频率的之字形运动，原因在于计算机仿真的离散特性，这样的影响叫做 抖振 (chattering)。