控制算法-运动学模型
概述
车辆横向运动学模型描述了车辆横向运动的数学模型,该模型不考虑车辆的受力情况。一般考虑运动学模型时,将车辆模型简化成单车模型(bicycle model)。

单车模型
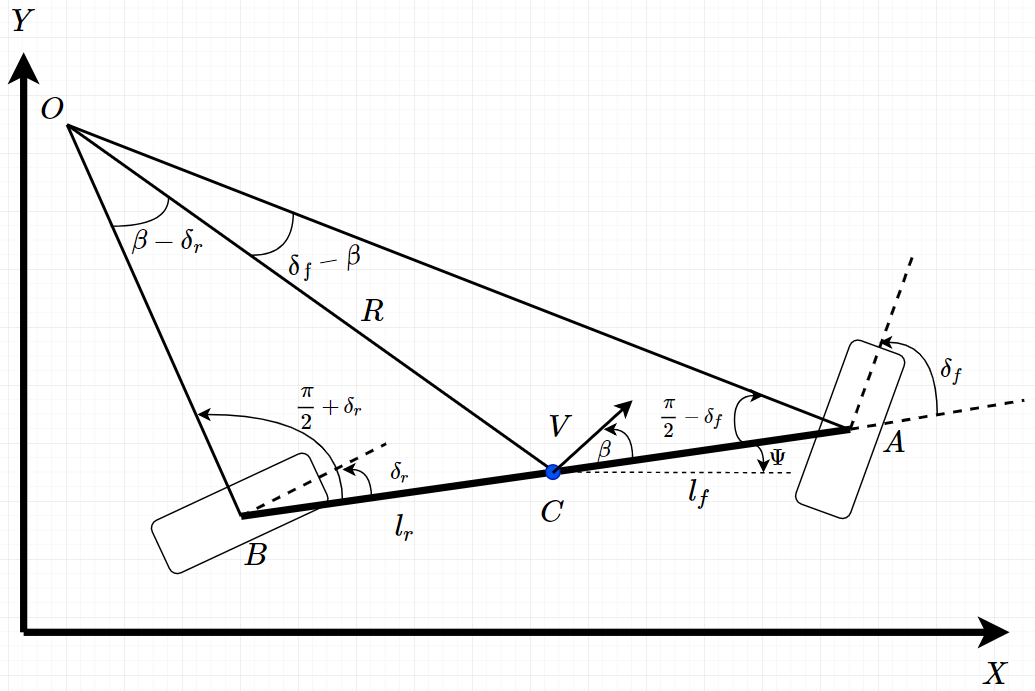
单车模型中:
左右轮等效为单个轮子 左右前轮合并为单个轮子,其中心点为\(A\)点,同样后轮等效后的中心点为\(B\)点。
转向角 前后轮的转向角用\(\delta_f\)和\(\delta_r\)表示,模型中前后轮都可以转向,对于只有前轮转向的系统,后轮转向角\(\delta_r\)可以设置为0.
重心 点\(C\)代表车辆的重心,\(A\)点和\(B\)点到重心的距离分别用\(l_f\)和\(l_r\)表示,轴距表示为\(L = l_f + l_r\)。
速度 车辆重心的速度用\(V\)表示,与车辆纵向轴的夹角为\(\beta\),该角度叫做车辆的滑移角。
运动描述 假设车辆平动,车辆运动状态可以用三个坐标量描述:\(X\) 、 \(Y\) 和 \(\psi\)。其中\((X,Y)\)代表车辆重心的位置,\(\Psi\)描述了车辆的方向。
条件假设 假设速度矢量\(V\)的方向在点\(A\)点和\(B\)点的方向与转向角的方向相同,换句话说,在A点的速度矢量与车辆纵轴的夹角为\(\delta_f\),同样\(B\)点的速度矢量与车辆纵轴的夹角为\(\delta_r\)。也就是说前后轮的滑移角都为0。该条件假设成立前提的是车辆速度很低(<5m/s),此时轮胎产生的横向力很小,可以忽略。
轨迹半径 点\(O\)代表车辆的瞬时旋转中心,线段\(AO\)与\(BO\)与前后两个转轮方向垂直,他们的交点即为\(O\)点,线段\(OC\)的长度代表车辆的轨迹半径\(R\)。
航迹角 车辆重心处的速度垂直于\(OC\),车辆速度矢量与车辆纵轴的夹角为\(\beta\),车辆的航向角为\(\psi\),则航迹角为\(\gamma = \psi + \beta\)。
运动方程
运动方程可以根据单车模型几何关系推导出,下面根据单车模型的几何关系,推导出车辆运动的微分方程。
姿态信息(偏航角)
三角形\(OCA\)根据正弦定理得
\[ \frac{\sin(\delta_f - \beta)}{l_f} = \frac{\sin(\frac{\pi}{2} - \delta_f)}{R} \tag{1} \]
同理,三角形\(OCB\)根据正弦定理可得
\[ \frac{\sin(\beta - \delta_r)}{l_r} = \frac{\sin(\frac{\pi}{2} + \delta_r)}{R} \tag{2} \]
根据和差定理,等式(1)得
\[ \frac{\sin(\delta_f)\cos(\beta) - \cos(\delta_f)\sin(\beta)}{l_f} = \frac{\cos(\delta_f)}{R} \tag{3} \]
同理,根据等式(2)得
\[ \frac{\cos(\delta_r)\sin(\beta) - \cos(\beta)\sin(\delta_r)}{l_r} = \frac{\cos(\delta_f)}{R} \tag{4} \]
等式(3)两边同时乘\(\frac{l_f}{\cos(\delta_f)}\)得
\[ \tan(\delta_f)\cos(\beta) - sin(\beta) = \frac{l_f}{R} \tag{5} \]
同理,等式(4)两边同时乘\(\frac{l_r}{\cos(\delta_r)}\)得
\[ sin(\beta) - \tan(\delta_r)\cos(\beta) = \frac{l_r}{R} \tag{6} \]
等式(5)和(6)相加得
\[ \{\tan(\delta_f) - \tan(\delta_r)\}\cos(\beta) = \frac{l_f + l_r}{R} \tag{7} \]
根据条件假设,车辆速度很低,车辆的轨迹半径变化就很慢。车辆偏航角的变化率(\(\dot{\psi}\))可以近似等于车辆的角速度(\(\omega\))。根据车辆角速度\(\omega = \frac{V}{R}\)得
\[ \dot{\psi} = \frac{V}{R} \tag{8} \]
将等式(8)带入等式(7)中,消除\(R\)项得
\[ \dot{\psi} = \frac{V\cos(\beta)}{l_f + l_r}\{\tan(\delta_f) - \tan(\delta_r)\} \tag{9} \]
上述等式一共三个输入变量:\(\delta_f\) 、\(\delta_r\)和\(V\)。其中\(\delta_f\)和\(\delta_r\)是车辆的转向角,可以通过车身传感器获得。\(V\)是一个外部变量,可以假设其为时变函数,可以从纵向控制中获得。
滑移角\(\beta\)的计算
等式(5)乘以\(l_r\),
\[ \tan(\delta_f)\cos(\beta)l_r - sin(\beta)l_r = \frac{l_f*l_r}{R} \tag{10} \]
等式(6)乘以\(l_f\)得
\[ sin(\beta)l_f - \tan(\delta_r)\cos(\beta)l_f = \frac{l_f*l_r}{R} \tag{11} \]
等式(10)和(11)相减得
\[ \cos(\beta)(l_f\tan(\delta_r) + l_r\tan(\delta_f)) = \sin(\beta)(l_f + l_r) \tag{12} \]
等式(12)两端同时乘以\(\frac{1}{\cos(\beta)}\)得
\[ \tan(\beta) = \frac{l_f\tan(\delta_r) + l_r\tan(\delta_f)}{l_f + l_r} \tag{13} \]
故取反三角函数得
\[ \beta = \arctan(\frac{l_f\tan(\delta_r) + l_r\tan(\delta_f)}{l_f + l_r} \tag{13}) \]
位置信息
根据单车模型得
\[ \dot{X} = V\cos(\beta + \psi) \tag{14} \] \[ \dot{Y} = V\sin(\beta + \psi) \tag{15} \]
补充
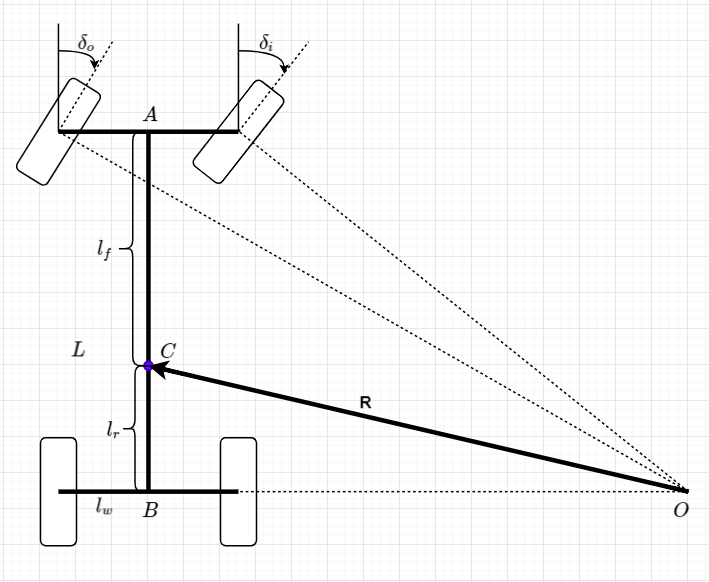
由上图可知,\(l_w\)为车轴宽度,为了避免与上述单车模型的转向角定义重复,使用\(\delta_o\)表示外部转向角,\(\delta_i\)表示内部转向角。由于轴距\(L = l_f + l_r\)远远小于轨迹半径\(R\),滑移角\(\beta\)接近于0。一般车辆模型后轴为固定轴,故\(\delta_r\)为0,所以等式(9)可以近似为
\[ \dot{\psi} = \frac{V}{L}\tan(\delta_f) \tag{16} \]
由于\(\delta_f\)很小
\[ \tan(\delta_f) \approx \delta_f \tag{17} \]
根据等式(8)和等式(16)得
\[ \frac{\dot{\psi}}{V} \approx \frac{\delta_f}{L} = \frac{1}{R} \tag{18} \]
故不区分前后轴,等效转向角为
\[ \delta = \frac{L}{R} \tag{19} \]
由于内外轮的转弯半径不同,根据等式(19),外轮转角为
\[ \delta_o = \frac{L}{R + \frac{l_w}{2}} \tag{20} \]
内轮转角为
\[ \delta_i = \frac{L}{R - \frac{l_w}{2}} \tag{21} \]
故前轮平均转向角为
\[ \delta = \frac{\delta_o + \delta_i}{2} = \frac{L}{R - \frac{l_w^2}{4R}} \tag{22} \]
由于\(\frac{l_w^2}{4R}\)项中,\(l_w\)远远小于\(R\),且\(l_w\)的二次项更小,故
\[ \frac{l_w^2}{4R} \cong 0 \tag{23} \]
所以等式(22)可以近似为
\[ \delta = \frac{L}{R} \tag{24} \]
比较等式(20)和(21)知,\(\delta_i\)始终大于\(\delta_o\),故
\[ \delta_i - \delta_o = \frac{L}{R - \frac{l_w}{2}} - \frac{L}{R + \frac{l_w}{2}} \quad\\ =\frac{Ll_w}{R^2 - \frac{l_w^2}{4}} \qquad\\ \cong \frac{L}{R^2}l_w = \delta^2\frac{l_w}{L} \tag{25} \]
根据等式(25)可知,前轮内外转向角的差值接近于平均转向角的二次方,所以当前轮转向角较大时,内外轮的转向角误差就越大。
结论
车辆运动模型基于单车模型推导,推导过程不考虑车辆受到的横向力,故该模型只适用于车辆速度很低的情形。
\[ a = \frac{mV^2}{R} \tag{26} \]
根据等式(26)知,速度很小时,车辆受到的向心力可以忽略不记,所以才有公式(8)的成立。所以当车辆的运动场景速度较低时,可以使用该模型描述车辆的运动。
微分方程形式
根据等式(9)、(14)和(15),对于前轮转向系统,\(\delta_r = 0\),可得
\[ \dot{X} = V\cos(\beta + \psi) \qquad\\ \dot{Y} = V\sin(\beta + \psi) \qquad\\ \dot{\psi} = \frac{V\cos(\beta)\tan(\delta_f)}{L} \]
其中
\[ \beta = \arctan(\frac{l_r\tan(\delta_f)}{l_f + l_r}) \]
假设车辆重心点在后轴中心点,则\(beta \cong 0\),由上述微分方程得
\[ \dot{X} = V\cos(\psi) \quad\\ \dot{Y} = V\sin(\psi) \quad\\ \dot{\psi} = \frac{V\tan(\delta_f)}{L} \]
参考
- " vehicle dynamics and control "