控制算法-动力学模型

概述

当车辆速度很高时，单车模型中前后轮的速度矢量不再与轮子方向一致。此时运动学模型就不能准确地描述车辆的运动状态，这就需要使用动力学模型对车辆进行建模。车辆单车模型中需要考虑两个维度的信息，这两个维度分别指代表车辆横向位置信息的\(y\)和表示车辆偏航角信息的\(\psi\)。下面分析过程中，先不考虑路堤角度的影响。

受力分析

平动

首先假设车辆为一个质点，对该质点进行受力分析，并根据牛顿第二定律得

\[ ma_y = F_{yf}+F_{yr} \tag{1} \]

其中，\(a_y\)为车辆重心处\(y\)轴方向的惯性加速度，\(F_{yf}\)和\(F_{yr}\)为前后轮横向受到的力。平动过程中，有两种力共同作用于加速度\(a_y\)：车辆延\(y\)轴产生的惯性加速度\(\ddot{y}\)和车辆绕旋转中心\(O\)旋转产生的向心加速度\(a_c=V_x\dot{\psi}\)。

\[ a_y = \ddot{y} + V_x\dot{\psi} \tag{2} \]

将公式(2)带入公式(1)得

\[ m(\ddot{y} + V_x\dot{\psi}) = F_{yf}+F_{yr} \tag{3} \]

转动

假设车辆为刚体，刚体绕重心转动，该运动过程使用力矩和转动惯量进行描述。 车辆绕z轴旋转产生的力矩平衡，对应的偏航动力学方程为

\[ I_z\ddot{\psi} = l_fF_{yf} - l_rF_{yr} \tag{4} \]

其中，\(l_f\)和\(l_r\)代表前后轮胎到重心的距离。

受力计算

上述等式(3)和(4)中都用到了轮胎横向受力情况\(F_{yf}\)和\(F_{yr}\)，根据实验结果知，轮胎的横向力与小的滑移角存在正比例的关系,滑移角是轮胎方向与车轮速度矢量之间的夹角。

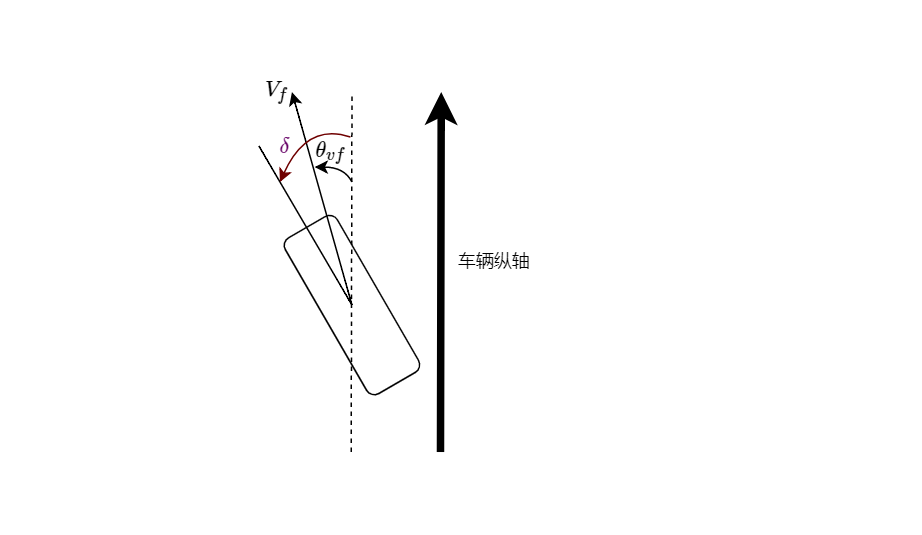
根据上图可知 \[ \alpha_f = \delta - \theta_{Vf} \tag{5} \]

其中，\(\theta_{Vf}\)代表速度矢量与车辆纵轴的夹角，\(\delta\)代表前轮转向角。 同理，由于后轮转向角\(\delta\)为0，故后轮滑移角为

\[ \alpha_r = -\theta_{Vr} \tag{6} \]

车辆前轮的横向力可以表示为

\[ F_{yf} = 2C_{\alpha f}(\delta - \theta_{Vf} ) \tag{7} \]

其中，比例常数\(C_{\alpha f}\)代表每个前轮的侧偏刚度。

同理后轮的横向力可以写为

\[ F_{yr} = 2C_{\alpha r}(-\theta_{Vr}) \tag{8} \]

其中，比例常数\(C_{\alpha r}\)代表每个后轮的侧偏刚度。

速度方向

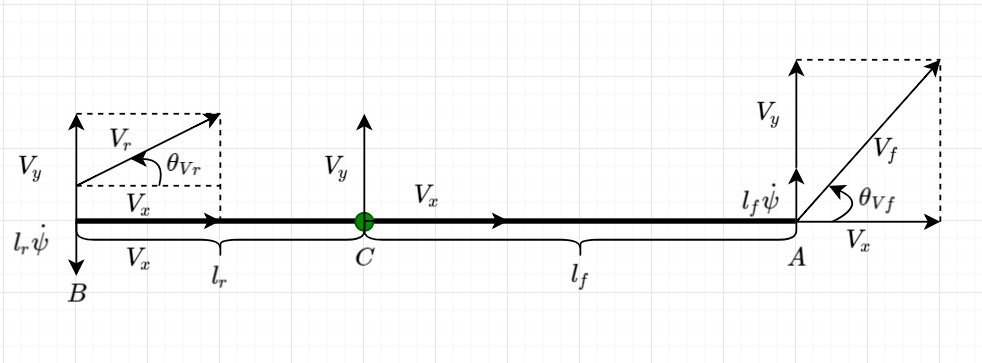
车辆平动产生的速度分量\(V_x\)和\(V_y\)，以及绕点\(C\)转动产生的线速度\(l_f\dot{\psi}\)和\(l_r\dot{\psi}\)组成。根据上图得

\[ \tan(\theta_{Vf})=\frac{V_y + l_f\dot{\psi}}{V_x} \tag{9} \]

\[ \tan(\theta_{Vr})=\frac{V_y - l_r\dot{\psi}}{V_x} \tag{10} \]

由于通常情况下速度矢量的夹角很小，可以使用小角度近似原理得 \[ \theta_{Vf}=\frac{\dot{y} + l_f\dot{\psi}}{V_x} \tag{11} \]

\[ \theta_{Vr}=\frac{\dot{y} - l_r\dot{\psi}}{V_x} \tag{12} \]

微分方程

将等式(7)、(8)、(9)和(10)代入等式(3)中得

\[ m(\ddot{y} + V_x\dot{\psi}) = 2C_{\alpha f}(\delta - \frac{\dot{y} + l_f\dot{\psi}}{V_x} ) +2C_{\alpha r}(-\frac{\dot{y} - l_r\dot{\psi}}{V_x}) \tag{13} \]

等式(13)左右两边同时除以\(m\)，分别提取 \(\ddot{y}\)、\(\dot{y}\)、\(\dot{\psi}\)和\(\delta\)项得

\[ \ddot{y} = -\frac{2C_{\alpha f } + 2C_{\alpha r}}{mV_x}\dot{y} - ( V_x + \frac{2C_{\alpha f}l_f- 2C_{\alpha r}l_r}{mV_x})\dot{\psi} + \frac{2C_{\alpha f}}{m} \delta \tag{14} \]

转化为矩阵形式如下

\[ \frac{\mathrm{d}}{\mathrm{d}t} \dot{y} = \begin{bmatrix} 0 & -\dfrac{2C_{\alpha f } + 2C_{\alpha r}}{mV_x} & 0 & - ( V_x + \dfrac{2C_{\alpha f}l_f- 2C_{\alpha r}l_r}{mV_x}) \end{bmatrix} \begin{bmatrix} y\\ \dot{y}\\ \psi\\ \dot{\psi} \end{bmatrix} + \frac{2C_{\alpha f}}{m}\delta \tag{15} \]

同理，将等式(7)、(8)、(9)和(10)代入等式(4)中得

\[ I_z\ddot{\psi} = 2l_fC_{\alpha f}(\delta - \frac{\dot{y} + l_f\dot{\psi}}{V_x} ) - 2l_rC_{\alpha r}(-\frac{\dot{y} - l_r\dot{\psi}}{V_x}) \tag{16} \]

等式(13)左右两边同时除以\(I_z\)，分别提取\(\dot{y}\)、 \(\ddot{\psi}\)、\(\dot{\psi}\)和\(\delta\)项得

\[ \ddot{\psi} = - \frac{2l_fC_{\alpha f} - 2l_rC_{\alpha r}}{I_zV_x}\dot{y} - \frac{2{l_f}^2C_{\alpha f} + 2{l_r}^2C_{\alpha r}}{I_zV_x}\dot{\psi} + \frac{2l_fC_{\alpha f}}{I_z}\delta\tag{17} \]

等效的矩阵形式为

\[ \frac{\mathrm{d}}{\mathrm{d}t} \dot{\psi} = \begin{bmatrix} 0 & - \dfrac{2l_fC_{\alpha f} - 2l_rC_{\alpha r}}{I_zV_x} & 0 & -\dfrac{2{l_f}^2C_{\alpha f} + 2{l_r}^2C_{\alpha r}}{I_zV_x} \end{bmatrix} \begin{bmatrix} y\\ \dot{y}\\ \psi\\ \dot{\psi} \end{bmatrix} + \frac{2l_fC_{\alpha f}}{I_z}\delta \tag{18} \]

根据等式(15)和(18)得

\[ \frac{\mathrm{d}}{\mathrm{d}t}\left \{ \begin{array}{cccc} y\\ \dot{y}\\ \psi\\ \dot{\psi} \end{array} \right\} = \begin{bmatrix} 0 & 1 & 0 & 0\\ 0 & -\dfrac{2C_{\alpha f } + 2C_{\alpha r}}{mV_x} & 0 & - ( V_x + \dfrac{2C_{\alpha f}l_f- 2C_{\alpha r}l_r}{mV_x})\\ 0 & 0 & 0 & 1\\ 0 & - \dfrac{2l_fC_{\alpha f} - 2l_rC_{\alpha r}}{I_zV_x} & 0 & -\dfrac{2{l_f}^2C_{\alpha f} + 2{l_r}^2C_{\alpha r}}{I_zV_x} \end{bmatrix} \begin{bmatrix} y\\ \dot{y}\\ \psi\\ \dot{\psi} \end{bmatrix}\\+ \begin{bmatrix} 0\\ \dfrac{2C_{\alpha f}}{m}\\ 0\\ \dfrac{2l_fC_{\alpha f}}{I_z} \end{bmatrix}\delta \tag{19} \]

• 注意：上述动力学方程的推导建立在车辆滑移角很小的情况下，这时的轮胎作用力与滑移角可以近似为线性关系。当滑移角很大时，轮胎作用力与滑移角就不再是线性关系。

参考

1. “vehicle dynamics and control”