双线性插值

发表于 更新于 分类于 阅读次数：

概述

线性差值在实际应用非常广泛，比如航空航天行业中广泛用到气动数据的插值，经常会用到三线性到四线性的插值，在汽车行业很多标定数据而需要使用双线性插值，本篇文章主要讲述双线性插值的实现方式。

重庆博物馆

应用场景

本文基于车辆扭矩标定的应用场景来说明2维线性插值的具体应用，根据车辆的控制原理可知，车辆的目标加速度与当前车速和发动机输出扭矩有关，因此对车辆扭矩进行标定后，我们就可以得到一个根据当前目标加速度和车速，获得车辆输出扭矩的关系表。 如下表所示，只选取了目标加速度为正的部分标定数据，其中横向表示速度(m/s)，纵向表示加速度(m/s2)，表中的数据代表汽车扭矩输出(Nm)。由于速度只采样了[0.1,0.2,0.3,0.4,0.5,0.6,0.7]这几个数值点的数据，加速度也只采样了[0.06,0.09,0.1,0.12,0.13,0.15,0.2,0.21,0.24,0.26]这几组数据点的数据，如果想得到中间任意数值的数值，就需要使用双线性插值算法来获得。

在这里插入图片描述

如下表所示，如果当前需求的目标加速度为0.094m/s2，当前车速为0.36m/s，想得到当前输出扭矩值，按照表格所圈出的扭矩值，进行多次线性插值，求得理想的输出扭矩。

在这里插入图片描述

双线性插值原理

双线性插值算法，是在线性插值的基础上进行多次插值的结果。 如下图所示，假设插值点\({(x_i,y_i)}\)的坐标点\(x_i\)和\(y_i\)范围满足，\(x_1\le x_i \le x_2\)，\(y_1\le y_i \le y_2\)，其中\((x_1,y_1)\)对应数值为\(z_1\)，\((x_2,y_1)\)对应数值为\(z_2\)，\((x_2,y_2)\)对应数值为\(z_3\)，\((x_1,y_2)\)对应数值为\(z_4\)。

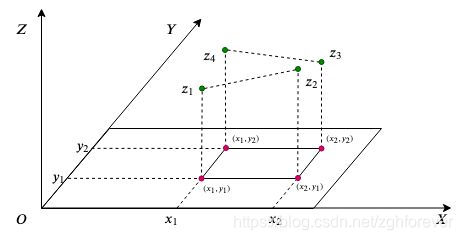
第一步，进行x轴方向的线性插值。当y取值\(y_1\)时，进行点\((x_1,z_1)\)和点\((x_2,z_2)\)之间的插值，得到插值点\((x_i,z5)\)；同理y取值\(y_2\)时，进行点\((x_1,z_4)\)和点\((x_2,z_3)\)之间的插值，可得第二个插值点\((x_i,z_6)\)。

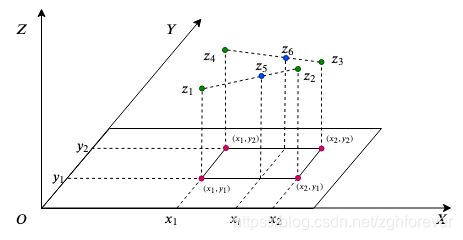
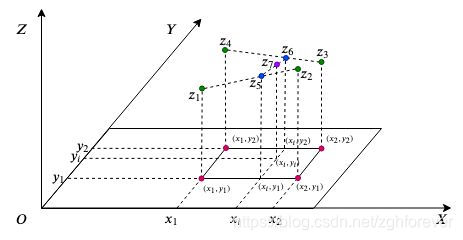
第二步，进行y轴方向的插值。依据新的插值点\((y_1,z5)\)和\((y_2,z_6)\)，进行线性插值，得到插值点\((x_i,y_i,z_7)\)。此时的点\((x_i,y_i,z_7)\)就是双线性插值的最终结果。

软件实现

本文基于c语言去实现插值算法，数据结构采用简单的数组结构，不使用C++的关联容器属性去实现数据表的存储。

数据表的存储结构

数据结构使用三个数组进行数组的存储，其中两个数组分别存储横向的速度值和纵向的加速度值，另一个数组存储对应的扭矩值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#define ACC_ARRAY_NUM       ( 10 )
#define VELOCITY_ARRAY_NUM  (  7 )
const float acc_table[ACC_ARRAY_NUM]           = {0.06f,0.09f,0.1f,0.12f,0.13f,0.15f,0.2f,0.21f,0.24f,0.26f};
const float velocity_table[VELOCITY_ARRAY_NUM] = {0.1f,0.2f,0.3f,0.4f,0.5f,0.6f,0.7f};

const float torque_table[ACC_ARRAY_NUM][VELOCITY_ARRAY_NUM]=
{
        {60,60,50,50,50,50,50},
        {140,140,100,60,50,50,50},
        {140,140,120,80,60,60,60},
        {140,140,140,100,60,60,60},
        {140,140,140,120,80,60,60},
        {140,140,140,140,100,60,60},
        {140,140,140,140,120,100,80},
        {140,140,140,140,140,120,100},
        {140,140,140,140,140,140,120},
        {140,140,140,140,140,140,140}
};

索引ID查找函数

输入参数 array ：需进行数值匹配查找的数组 输入参数 num ：数组的长度 输入参数 input ：需要匹配的值 输出参数 before ：匹配值的前数组边界ID 输出参数 before ：匹配值的后数组边界ID

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
void ArrayIndexFind(float *array,uint16_t num,float input,uint16_t *before,uint16_t *after)
{
    uint16_t min_index,max_index;
    uint16_t middle_index;
    min_index = 0;
    max_index = num - 1;

    while( (max_index - min_index) > 1)
    {
        middle_index = (min_index + max_index) / 2 ;
        if(input < array[middle_index])
        {
            max_index = middle_index;
        }
        else
        {
            min_index = middle_index;
        }
    }
    *before = min_index;
    *after  = max_index;
}

数据插值函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
float InterpolateValue(float x,float x0,float y0,float x1,float y1)
{
    if(fabs(x - x0) < kDoubleEpsilon)
    {
        return y0;
    }
    else if(fabs(x - x1) < kDoubleEpsilon)
    {
        return y1;
    }
    else
    {
        return y0 + (y1 - y0)*(x - x0)/ (x1 - x0);
    }
}

线性差值函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
float Interpolation::InterpolationYZ(float y,float *y_tb,uint16_t y_num,float *z_tb)
{
    float max_y = y_tb[y_num - 1];
    float min_y = y_tb[0];
    uint16_t y_before,y_after;

    if(y >= (max_y - kDoubleEpsilon))
    {
        return z_tb[y_num - 1];
    }
    if(y <= (min_y + kDoubleEpsilon))
    {
        return z_tb[0];
    }

    ArrayIndexFind(y_tb,y_num,y,&y_before,&y_after);
    return InterpolateValue(y,y_tb[y_before],z_tb[y_before],y_tb[y_after],z_tb[y_after]);
}

双线性插值函数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
float Interpolation2D(float x,float y,float *x_tb,uint16_t x_num,float *y_tb,uint16_t y_num,float *z_tb)
{
    float max_x = x_tb[x_num - 1];
    float min_x = x_tb[0];

    uint16_t x_before,x_after;
    uint16_t z_before_value,z_after_value;
    if(x > (max_x - kDoubleEpsilon))
    {
        return InterpolationYZ(y,y_tb,y_num, (z_tb + (x_num - 1)*y_num));
    }
    if(x < (min_x + kDoubleEpsilon))
    {
        return InterpolationYZ(y,y_tb,y_num, z_tb);
    }

    ArrayIndexFind(x_tb,x_num,x,&x_before,&x_after);

    z_before_value = InterpolationYZ(y,y_tb,y_num, (z_tb + x_before * y_num));
    z_after_value  = InterpolationYZ(y,y_tb,y_num, (z_tb + x_after  * y_num));
    return InterpolateValue(x,x_tb[x_before],z_before_value,x_tb[x_after],z_after_value);
}